Evento intersezione

L'evento intersezione si verifica quando due o più eventi, che appartengono allo stesso insieme universo, avvengono contemporaneamente. $$ E_1 \cap E_2 ​$$

Questa tipologia di eventi sono noti anche come "prodotto logico".

L'intersezione degli eventi mi permette di valutare la probabilità che più eventi avvengano contemporaneamente.

Usando la teoria della probabilità e della statistica, gli eventi sono spesso rappresentati come intersezione di insiemi.

 

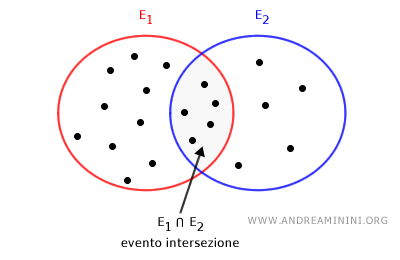
Nota. La notazione per gli eventi, pur usando simboli simili alla teoria degli insiemi, non rappresenta direttamente l'operazione di intersezione o unione tra insiemi ma piuttosto la simultaneità (evento intersezione) o l'alternativa tra eventi (evento unione).

Fornisce uno strumento per analizzare scenari in cui più condizioni devono essere soddisfatte simultaneamente.

Il teorema della probabilità composta

Per calcolare la probabilità del prodotto logico di due eventi \( E_1 \) ed \( E_2 \), cioè dell’evento \( E_1 \cap E_2 \), devo distinguere tra due casi fondamentali.

• Eventi indipendenti
  Due eventi si dicono stocasticamente indipendenti quando il verificarsi di uno non influisce sulla probabilità dell’altro. In questo caso, la probabilità dell’evento composto è il prodotto delle probabilità dei singoli eventi: \[
  p(E_1 \cap E_2) = p(E_1)\cdot p(E_2) \]
• Eventi dipendenti
  Se due eventi sono dipendenti, il verificarsi di uno modifica la probabilità dell’altro. La probabilità dell’evento composto si ottiene moltiplicando la probabilità del primo evento per la probabilità condizionata del secondo rispetto al primo: \[ p(E_1 \cap E_2) = p(E_1)\cdot p(E_2 \mid E_1) \] In questo modo posso calcolare la probabilità di un evento composto anche quando non è possibile fare un calcolo diretto su \( p(E_1 \cap E_2) \), ma è più semplice stimare \( p(E_1) \) e \( p(E_2 \mid E_1) \).
  

  Nota. La probabilità condizionata \( p(E_2 \mid E_1) \) è definita come: \[ p(E_2 \mid E_1) = \frac{p(E_1 \cap E_2)}{p(E_1)} \quad \text{con } p(E_1)\neq 0 \] Da questa definizione si ricava direttamente la formula della probabilità composta per eventi dipendenti. \[ p(E_1 \cap E_2) = p(E_1)\cdot p(E_2 \mid E_1) \] Questa formula ha carattere generale, perché include anche il caso degli eventi indipendenti. Infatti, quando due eventi sono indipendenti, la probabilità condizionata coincide con la probabilità dell’evento singolo \( p(E_2 \mid E_1) = p(E_2)\). Quindi, sostituendo nella formula generale si ottiene: \[ p(E_1 \cap E_2) = p(E_1)\cdot p(E_2) \]

E se gli eventi sono più di due?

Se gli eventi da considerare sono tre, la probabilità del prodotto logico si calcola applicando successivamente la probabilità condizionata:

\[ p(E_1 \cap E_2 \cap E_3) = p(E_1)\cdot p(E_2 \mid E_1)\cdot p(E_3 \mid E_1 \cap E_2) \]

Nel caso in cui tutti gli eventi siano indipendenti tra loro, la formula si riduce al semplice prodotto delle probabilità:

\[ p(E_1)\cdot p(E_2)\cdot p(E_3) \]

Un esempio pratico

Ad esempio, una classe di 30 studenti. Di questi studenti:

• 15 praticano il calcio
• 10 praticano il nuoto
• 5 praticano sia il calcio sia il nuoto

Definisco due eventi E₁​ ed E₂​

$$ E_1​: \ \text{Lo studente pratica il calcio.} $$ $$ E_2​: \ \text{Lo studente pratica il nuoto.} $$

L'evento intersezione tra E₁​ ed E₂​ rappresenta gli studenti che praticano sia il calcio sia il nuoto.

$$ E_1 \cap E_2 ​ : \ \text{Lo studente pratica sia il calcio sia il nuoto.} $$

Dai dati forniti, so già che ci sono 5 studenti che rientrano in questa categoria.

Pertanto, l'evento intersezione E₁∩E₂​ si verifica per questi 5 studenti.

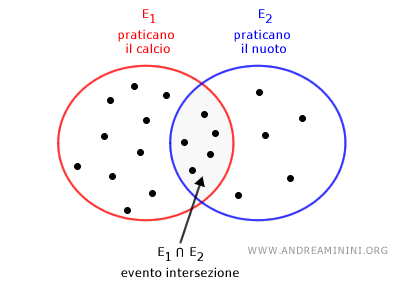
In termini insiemistici, questo corrisponde ai casi in cui ci sono elementi comuni sia all’insieme E₁ che all'insieme E₂.

Esempio 2

Considero il lancio di una moneta e il lancio di un dado.

Definisco gli eventi:

• \( E_1 \): esce testa nel lancio della moneta
• \( E_2 \): esce il numero 6 nel lancio del dado

I due eventi sono stocasticamente indipendenti, perché l’esito della moneta non influisce sull’esito del dado.

Le probabilità dei singoli eventi sono:

\[ p(E_1) = \tfrac{1}{2} \]

\[ p(E_2) = \tfrac{1}{6} \]

Poiché gli eventi sono indipendenti, la probabilità dell’evento composto è:

\[ p(E_1 \cap E_2) = p(E_1)\cdot p(E_2) \]

\[ p(E_1 \cap E_2) = \tfrac{1}{2}\cdot \tfrac{1}{6} = \tfrac{1}{12} = 0.083 = 8.3 \% \]

Pertanto, la probabilità dell'evento composto è circa del 8.3%.

Esempio 3

Considero un’urna che contiene 3 palline rosse e 2 palline blu.

Qual è la probabilità di estrarre due palline rosse in successione senza reinserimento?

In questo caso l'estrazione della prima pallina modifica la probabilità della seconda estrazione, perché non la reinserisco nell'urna. Quindi, gli eventi sono dipendenti.

Definisco gli eventi:

• \( E_1 \): la prima pallina estratta è rossa
• \( E_2 \): la seconda pallina estratta è rossa

La probabilità del primo evento è $ \frac{3}{5} $ perché inizialmente nell'urna ci sono 3 palline rosse su 5.

\[ p(E_1) = \tfrac{3}{5} \]

Se la prima pallina è rossa, nell’urna restano 2 palline rosse su 4 totali.

Quindi, la probabilità condizionata del secondo evento $ E_2 $ rispetto al primo $ E_1 $ è:

\[ p(E_2 \mid E_1) = \tfrac{2}{4} = \tfrac{1}{2} \]

La probabilità che entrambe le palline estratte siano rosse è:

\[ p(E_1 \cap E_2) = p(E_1)\cdot p(E_2 \mid E_1) \]

\[ p(E_1 \cap E_2)  = \tfrac{3}{5}\cdot \tfrac{1}{2} = \tfrac{3}{10} = 0.3 = 30% \]

Complessivamente, la probabilità di estrarre due palline rosse in successione è del 30%.

Nota. In questo caso non ho potuto usare il prodotto delle probabilità dei singoli eventi, perché l’estrazione della prima pallina ha modificato la probabilità della seconda.

E così via.