Probabilità degli eventi

A ogni evento E di uno spazio degli esiti S è associata una probabilità dell'evento P(E).

Quando un esperimento è ripetuto un gran numero di volte, un evento tende a presentarsi con una frequenza relativa empirica costante pari alla sua probabilità P(E).

La probabilità di un evento deve rispettare alcuni assiomi.

1. Assioma 1
   La probabilità dell'evento è un numero compreso tra 0 e 1. $$ 0 \le P(E) \le 1 $$
2. Assioma 2
   La somma delle probabilità degli eventi in uno spazio degli esiti è pari a 1. $$ P(S)=1 $$
3. Assioma 3
   Se gli eventi dello spazio degli esiti è un insieme finito composto da eventi mutuamente esclusivi, ossia se si presenta un evento E₁ non possono verificarsi gli altri, allora la probabilità che si presenti almeno un evento è uguale alla somma delle loro probabilità. $$ P( U_{i=1}^n E_i ) = \sum_{i=1}^n P(E_i) $$ Quando due eventi non sono mutuamente esclusivi possono verificarsi contemporaneamente. In questo caso, per calcolare la probabilità che si verifichi un evento o l'altro occorre rettificare la formula $$ P(E∪F) = P(E)+P(F)-P(E⋂F) $$

   Esempio. Lanciando un dado, l'evento E si verifica quando esce 2 mentre l'evento F si verifica quando esce 1. Le probabilità degli eventi sono $ P(E)=\frac16 $ e $ P(F)=\frac16 $. I due eventi sono mutuamente esclusivi. Quindi, la probabilità che esca 1 o 2 è pari alla somma $$ P(E)+P(F)=\frac16+\frac16=\frac13 $$

Teorema della probabilità totale

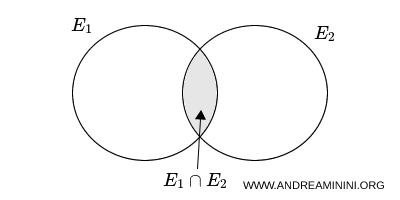
La probabilità della somma logica (unione) di due eventi \( E_1 \) ed \( E_2 \) è uguale alla somma delle probabilità dei singoli eventi, diminuita della probabilità del loro evento intersezione. \[ p(E_1 \cup E_2) = p(E_1) + p(E_2) - p(E_1 \cap E_2) \]

Il termine \( p(E_1 \cap E_2) \) viene sottratto perché, sommando \( p(E_1) \) e \( p(E_2) \), gli esiti comuni ai due eventi verrebbero contati due volte.

Caso particolare: eventi incompatibili

Due eventi si dicono incompatibili (o mutuamente esclusivi) se non possono verificarsi contemporaneamente. In questo caso l’intersezione è l’insieme vuoto:

\[ E_1 \cap E_2 = \emptyset \]

Quindi la probabilità dell'evento intersezione è nulla

\[ p(E_1 \cap E_2) = 0 \]

La formula generale si riduce allora a:

\[ p(E_1 \cup E_2) = p(E_1) + p(E_2) \]

Nota. La formula vale per qualunque coppia di eventi. Il caso degli eventi incompatibili non è un nuovo teorema, ma una semplice conseguenza della formula generale quando non esistono esiti in comune tra \( E_1 \) ed \( E_2 \).

Esempi

Esempio 1 (eventi incompatibili)

Lancio un dado a sei facce e considero due eventi.

• \( E_1 = \) “esce 1”
• \( E_2 = \) “esce 6”

I due eventi sono incompatibili perché non possono verificarsi contemporaneamente.

Le probabilità sono:

\[ p(E_1) = \frac{1}{6}, \quad p(E_2) = \frac{1}{6} \]

Poiché \( E_1 \cap E_2 = \emptyset \), vale:

\[ p(E_1 \cup E_2) = p(E_1) + p(E_2) = \frac{1}{6} + \frac{1}{6} = \frac{2}{6} = \frac{1}{3} = 0.\overline{3} \]

La probabilità che si verifichi almeno uno dei due eventi è 0.33, circa il 33,3% in percentuale.

In questo caso il risultato coincide con la semplice somma delle singole probabilità degli eventi perché i due eventi non possono verificarsi contemporaneamente, la probabilità dell'evento intersezione è nulla.

Esempio 2 (eventi compatibili)

Lancio un dado a sei facce e considero questi due eventi:

• \( E_1 = \) “esce un numero pari”
• \( E_2 = \) “esce un numero maggiore di 3”

Gli esiti possibili sono:

• Numeri pari: \( \{ 2,4,6 \} \)
• Numeri maggiori di 3: \( \{ 4,5,6 \} \)

L’intersezione è:

\[ E_1 \cap E_2 = \{ 4,6 \} \]

Le probabilità sono:

\[ p(E_1) = \frac{3}{6}, \quad p(E_2) = \frac{3}{6}, \quad p(E_1 \cap E_2) = \frac{2}{6} \]

Applicando la formula generale.

\[ p(E_1 \cup E_2) = \frac{3}{6} + \frac{3}{6} - \frac{2}{6} = \frac{4}{6} = \frac{2}{3} =0.\overline{6} \]

In questo caso è necessario sottrarre l’intersezione perché gli esiti comuni \( \{ 4,6 \} \) verrebbero altrimenti contati due volte.

Quindi, la probabilità che si verifichi almeno uno dei due eventi è 0.66, circa il 66,6% in percentuale.

Esempio 3

Il 35% della popolazione ha un'automobile (evento E), il 10% ha una moto (evento F). Il 5% ha sia un'automobile che una moto (E ⋂ F).

Qual è la percentuale di popolazione che non possiede né un'automobile, né una moto?

Per prima cosa calcolo la percentuale di persone che ha almeno un'auto o una moto.

$$ P(E ∪ F) = P(E)+P(F)-P(E ⋂ F) = 0.35+0.10-0.05 = 0.40 $$

Quindi, il 40% della popolazione possiede almeno un'automobile o una moto.

Di conseguenza, il 60% della popolazione non possiede né una moto, né un'automobile.

$$ 1 - 0.4 = 0.6 $$

Osservazioni

Ecco alcune osservazioni pratiche

• Probabilità della somma logica di tre eventi
  Nel caso di tre eventi \( E_1 \), \( E_2 \), \( E_3 \), la formula della probabilità dell’unione tiene conto di tutte le sovrapposizioni possibili tra gli eventi. La relazione diventa: \[ \begin{aligned} p(E_1 \cup E_2 \cup E_3) &= p(E_1) + p(E_2) + p(E_3) \\ &\quad - p(E_1 \cap E_2)  - p(E_1 \cap E_3) - p(E_2 \cap E_3) \\ &\quad + p(E_1 \cap E_2 \cap E_3) \end{aligned} \] In questo caso, i termini \( p(E_1) + p(E_2) + p(E_3) \) sommano le probabilità dei singoli eventi. Le probabilità delle intersezioni a due a due vengono sottratte perché contate due volte. La probabilità dell’intersezione tripla $ p(E_1 \cap E_2 \cap E_3) $ viene aggiunta perché era stata sottratta tre volte nei passaggi precedenti.
  
  

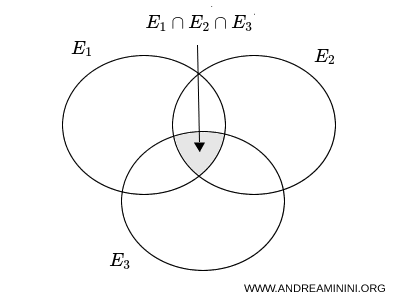
  Nota. La formula segue lo stesso principio del caso di due eventi. Più eventi si considerano, più è necessario correggere il conteggio delle parti comuni per evitare errori di sovrastima.

• Dato un evento E, per calcolare la probabilità che non si verifichi devo considerare l'insieme complementare E^c. L'insieme complementare E^c comprende tutti gli eventi dello spazio degli esiti diversi da E. Quindi, la probabilità che l'evento E non si verifichi è pari a uno meno la probabilità dell'evento. $$ P(E^c) = 1 - P(E) $$

  Esempio. Se lo spazio degli esiti del lancio di un dado è composto da sei eventi, uno per ogni faccia. L'evento E è l'uscita del numero 2 e ha probabilità P(E)=1/6. Pertanto, la probabilità che non si verifichi è pari a P(E^c)=1-1/6=5/6.

E così via