Probabilità condizionata
La probabilità condizionata è la probabilità di un evento E quando un altro evento accessorio A si è già verificato $$ P(E|A) $$ Si legge probabilità di E dato A.
- Se i due eventi sono eventi dipendenti la probabilità condizionata di E dato A è la seguente $$ P(E|A) = \frac{P(E \cap A)}{P(A)} $$
- Se i due eventi sono eventi indipendenti, la probabilità dell'evento E è sempre la stessa perché è indipendente dall'evento A $$ P(E|A)=P(E) $$
La probabilità condizionata misura la probabilità dell'evento E (evento condizionato) se si è già verificato l'evento A (evento accessorio o condizionante).
E' anche detta probabilità a posteriori.
Se gli eventi sono eventi dipendenti, la probabilità condizionata p(E|A) si misura tramite questa formula:
$$ P(E|A) = \frac{P(E \cap A)}{P(A)} $$
Dove E è l'evento condizionato e A è l'evento condizionante.
- P(E|A) è la probabilità condizionata di E dato A.
- P(E∩A) è la probabilità che entrambi gli eventi E e A si verifichino (probabilità congiunta).
- P(A) è la probabilità dell'evento condizionante A.
La probabilità condizionata aiuta a ricalcolare la probabilità dell'evento E tenendo conto dell'informazione addizionale che l'evento A è già accaduto.
Nota. La probabilità dell'evento condizionante P(A) non deve essere nulla. In caso contrario si cadrebbe in una divisione per zero. $$ P(A) \ne 0 $$
I due eventi possono essere correlati positivamente o negativamente
- Se P(E|A)>P(E) i due eventi sono correlati positivamente.
- Se P(E|A)<P(E) i due eventi sono correlati negativamente.
Se i due eventi sono eventi indipendenti la probabilità condizionata di uno non è influenzata dall'occorrenza dell'altro. In questo caso, la probabilità dell'evento E non cambia.
$$ P(E∣A)=P(E) $$
- Esempio. Ecco qualche esempio pratico
- La probabilità che piova (evento E) sapendo che ieri ha piovuto (evento A).
- La probabilità di non passare un esame (evento E) se uno studente non ha studiato abbastanza (evento A).
- La probabilità di subire un infarto (evento E) se il paziente è anziano (evento A).
Un esempio pratico
Esempio 1
Qual è la probabilità di pescare un asso da un mazzo di carte, sapendo che la carta pescata è di cuori?
In questo caso l'evento condizionato E è "pescare un asso" mentre l'evento condizionante A è "pescare una carta di cuori".
In un mazzo standard di carte da gioco, ci sono 52 carte in totale. Tra queste, ci sono 4 assi e 13 carte di cuori (incluso un asso di cuori).
La probabilità di pescare un carta di cuori è p(A)= 13/52
$$ p(A) = \frac{13}{52} $$
La probabilità di pescare un asso è P(E)=4/52 ossia 1 su 13
$$ p(E) = \frac{4}{52} = \frac{1}{13} $$
Calcolo la probabilità $ p(E∩A) $ che i due eventi si verifichino insieme
$$ p(E∩A) = \frac{13}{52} \cdot \frac{1}{13} = \frac{1}{52} $$
A questo punto uso la formula della probabilità condizionata:
$$ P(E|A) = \frac{P(E \cap A)}{P(A)} $$
$$ P(E|A) = \frac{ \frac{1}{52} }{ \frac{13}{52} } $$
$$ P(E|A) = \frac{1}{52} \cdot \frac{52}{13} $$
$$ P(E|A) = \frac{1}{13} $$
$$ P(E|A) = 0.0769 $$
Quindi, la probabilità di pescare un asso, sapendo che la carta pescata è di cuori, è circa 0.076 o 7.6%.
Questo significa che, una volta saputo che la carta estratta è una carta di cuori, c'è una probabilità del 7.7% che sia anche un asso.
Esempio 2
Il 70% della popolazione porta i pantaloni, il 30% la gonna.

La probabilità che un passante a caso abbia i pantaloni è p(A)=70%
$$ p(E)=70% $$
Dove E è l'evento che passi una persona con i pantaloni.
Sapendo che il prossimo passante è una donna (evento condizionante A), devo calcolare la probabilità condizionata p(E|A) dell'evento E noto A.
$$ P(E|A) = \frac{P(E \cap A)}{P(A)} $$
La probabilità che passi una donna è del 60% perché 6 persone su 10 sono donne p(A)=0.6

La probabilità che passi una donna con i pantaloni (E⋂A) è del 30% perché 3 persone su 10 sono donne che portano i pantaloni p(E⋂A)=0.3

Quindi, la probabilità condizionata è
$$ P(E|A) = \frac{0.3}{0.6} = 0.50 $$
La probabilità che il prossimo passante porti i pantaloni (evento E) sapendo che il prossimo passante è una donna (evento A) è del 50%.

Esempio 3
Il lancio di due dadi genera uno spazio degli esiti S composto da 36 esiti.
$$ (i,j) $$
Dove i=1,2,3,4,5,6 è la faccia ottenuta dal primo dado e j=1,2,3,4,5,6 è quella del secondo dato.
$$ S = \begin{pmatrix} (1,1) & (1,2) & (1,3) & (1,4) & (1,5) & (1,6) \\ (2,1) & (2,2) & (2,3) & (2,4) & (2,5) & (2,6) \\ (3,1) & (3,2) & (3,3) & (3,4) & (3,5) & (3,6) \\ (4,1) & (4,2) & (4,3) & (4,4) & (4,5) & (4,6) \\ (5,1) & (5,2) & (5,3) & (5,4) & (5,5) & (5,6) \\ (6,1) & (6,2) & (6,3) & (6,4) & (6,5) & (6,6) \end{pmatrix} $$
Se il primo dado è pari a 4 (evento condizionante A) qual è la probabilità che esca un risultato complessivo pari a 7 (evento condizionato E)?
$$ P(E|A)= \frac{P(E \cap A)}{P(A)} $$
La probabilità P(E⋂A) che la somma sia pari a 7 e il primo dado sia pari a 4 è 1/36 perché l'unico esito che soddisfa questa ipotesi è l'esito (4,3) in uno spazio S composto da 36 esiti complessivi.
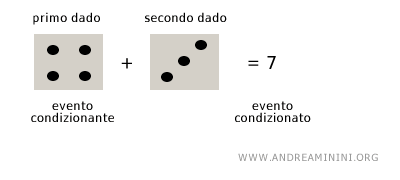
Quindi P(E⋂A)=1/36
$$ P(E|A)= \frac{\frac{1}{36}}{P(A)} $$
La probabilità che esca l'evento condizionante ossia 4 nel secondo dado è P(A)=1/6 perché il dado ha sei facce.
$$ P(E|A)= \frac{\frac{1}{36}}{\frac{1}{6}} $$
Svolgo i calcoli algebrici
$$ P(E|A)= \frac{\frac{1}{36}}{\frac{1}{6}} = \frac{1}{36} \cdot \frac{6}{1} = \frac{1}{6} $$
Pertanto, la probabilità condizionata che la somma sia uguale a 7 dato il risultato del primo dado pari a 4 è P(E|A)=1/6.
Dimostrazione
Considero due eventi $ E_1 $ ed $ E_2 $ appartenenti allo stesso spazio degli eventi $ U $
$$ E_1 \subset U $$
$$ E_2 \subset U $$
Ogni evento è un sottoinsieme non vuoto.
- In $ E_1 $ ci sono $ n_1 = |E_1| $ esiti
- In $ E_2 $ ci cono $ n_2 = |E_2| $ esiti
Per ipotesi l'intersezione dei due sottoinsiemi non è nulla
$$ E_1 \cap E_2 \ne \emptyset $$
Dal punto di vista dei diagrammi di Eulero-Venn si verifica questa situazione:
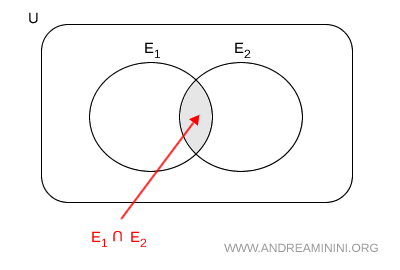
L'intersezione $ E_1 \cap E_2 $ contiene gli esiti positivi $ k $ di $ E_1 $ quando $ E_2 $ si è verificato.
La probabilità condizionata dell'evento $ E_1 $ rispetto a $ E_2 $ è il rapporto tra il numero degli esiti positivi $ k = |E_1 \cap E_2| $ e quello degli esiti positivi $ n_2 = |E_2| $
$$ P(E_1|E_2) = \frac{k}{n_2} $$
Divido sia il numeratore che il denominatore per il numero dei campioni $ n $ dello spazio degli eventi $ U $
$$ P(E_1|E_2) = \frac{ \frac{k}{n} }{ \frac{n_2}{n} } $$
Poiché $ P(E_2) = \frac{n_2}{n} $ e $ P(E_1 \cap E_2) = \frac{k}{n} $
$$ P(E_1|E_2) = \frac{ \frac{k}{n} }{ \frac{n_2}{n} } = \frac{P(E_1 \cap E_2)}{P(E_2)} $$
Si ottiene la formula fondamentale della probabilità condizionata.
$$ P(E_1|E_2) = \frac{P(E_1 \cap E_2)}{P(E_2)} $$
Questa relazione mostra che la probabilità condizionata misura la probabilità dell’evento $ E_1 $ restringendo lo spazio degli eventi al solo sottoinsieme $ E_2 $.
Esempio numerico. Considero un’urna con 10 palline numerate da 1 a 10. L’estrazione è una sola pallina, e tutte le palline hanno la stessa probabilità di uscire. Lo spazio degli eventi è $$ U = \{1,2,3,4,5,6,7,8,9,10 \} $$ Il numero totale degli esiti è $$ n = 10 $$ Definisco due eventi.
- Evento \( E_1 \): esce un numero pari $$ E_1 = \{2,4,6,8,10\} $$
- Evento \( E_2 \): esce un numero maggiore di 5 $$ E_2 = \{6,7,8,9,10\} $$
Entrambi gli eventi sono non vuoti e appartengono allo stesso spazio \( U \).
In \( E_1 \) ci sono $ n_1 = 5 $ mentre in \( E_2 \) ci sono $ n_2 = 5 $
L’intersezione dei due eventi non è vuota.
$$ E_1 \cap E_2 = \{6,8,10 \} $$
Il numero di esiti comuni è $ k = 3 $
La probabilità condizionata di \( E_1 \) rispetto a \( E_2 \) è
$$ P(E_1 \mid E_2) = \frac{k}{n_2} = \frac{3}{5} $$
Calcolo ora le probabilità assolute.
$$ P(E_2) = \frac{n_2}{n} = \frac{5}{10} = \frac{1}{2} $$
$$ P(E_1 \cap E_2) = \frac{k}{n} = \frac{3}{10} $$
Applicando la formula della probabilità condizionata ottengo
$$ P(E_1 \mid E_2) = \frac{P(E_1 \cap E_2)}{P(E_2)} = \frac{\frac{3}{10}}{\frac{1}{2}} = \frac{3}{5} $$
Il risultato coincide con il calcolo diretto, e mostra che la probabilità condizionata si ottiene restringendo lo spazio degli eventi all’evento \( E_2 \).
E così via.
