Evento
Un evento è un avvenimento descritto da una proposizione che può verificarsi oppure no.
Esistono tre categorie fondamentali di eventi.
- Eventi certi
Si verificano con certezza. Ad esempio, se lancio il dado uscirà sempre un numero compreso tra 1 e 6. - Eventi impossibili
Non possono mai verificarsi. Ad esempio, se lancio il dado non potrà mai uscire il numero 7. - Eventi aleatori
Sono eventi incerti, dipendono dal caso e possono accadere ma senza certezza. Ad esempio, se lancio il dado potrei ottenere il numero 3 oppure no.Nota. Del resto, lo stesso termine "aleatorio" dipende da "alea" che in latino vuol dire proprio "dado".
Gli eventi aleatori sono centrali in statistica, perché introducono il concetto di probabilità.
Un evento aleatorio può essere interpretato come l'esito (risultato) di un esperimento casuale (detto "esperimento aleatorio") e ogni esito possibile è detto campione, oppure evento elementare.
L'insieme di tutti i risultati possibili è detto universo degli esiti, spazio campionario, spazio o insieme degli esiti.
In generale, nel calcolo delle probabilità un evento E è un sottoinsieme dell'insieme degli esiti. L'evento contiene soltanto gli esiti possibili che lo verificano.
Un esempio di evento
Nel lancio di un dado lo spazio degli esiti è un insieme finiti con 6 elementi (esiti possibili).
$$ S = \{ 1, 2, 3, 4, 5, 6 \} $$
Un esempio di evento E è l'uscita di un numero pari.
L'evento E è un insieme con tre esiti.
$$ E = \{ 2, 4, 6 \} $$
Un altro evento è l'uscita dei numeri dispari
Anche l'evento D è un insieme con tre esiti.
$$ D = \{ 1, 3, 5 \} $$
Un altro evento è l'uscita di un numero inferiore a 3
L'evento F è un insieme con due esiti
$$ F = \{ 1, 2 \} $$
I tre eventi D, E, F posso rappresentarli graficamente con un diagramma di Venn.
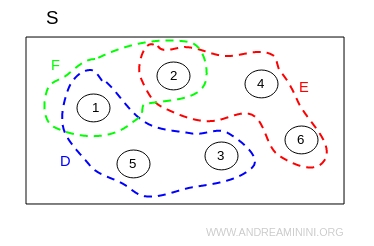
Dove S è lo spazio degli esiti e i cerchi numerati sono gli esiti.
L'evento vuoto
Se un evento non ha nessun elemento (esito) è detto evento vuoto e si indica con il simbolo degli insiemi vuoti
Ad esempio, l'evento F dei numeri negativi del lancio di un dado è un evento vuoto perché non contiene esiti possibili.
$$ F = \{ \} = Ø $$
Relazione di inclusione e uguaglianza
Quando tutti gli esiti di un evento A appartengono anche a un altro evento B, si dice che A è contenuto in B $$ A ⊂ B $$
I due eventi sono in una relazione di inclusione.
Questo vuol dire che se si verifica A, si verifica anche B.
Esempio. L'evento G contiene tutti gli esiti che diano un punteggio pari a 2 con il lancio di un dado $$ G = \{ 2 \} $$ L'evento G è contenuto nell'evento E dei numeri pari. $$ G ⊂ E $$ ossia $$ \{ 2 \} ⊂ \{ 2, 4, 6 \} $$ Visto con i diagrammi di Venn
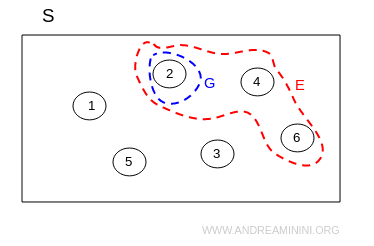
Se entrambi gli eventi hanno una relazione di inclusione reciproca, vuol dire che gli insiemi hanno gli stessi esiti.
$$ A ⊂ B, A ⊃ B \Leftrightarrow A=B $$
In questo caso i due eventi sono in relazione di uguaglianza.
L'unione e l'intersezione degli eventi
L'unione degli eventi EUD comprende tutti gli esiti degli eventi E e D. Si verifica quando almeno uno degli eventi di E o D si verifica.
$$ E \cup D = \{ 2,4,6 \} \cup \{ 1,3,5 \} = \{ 1,2,3,4,5,6 \} $$
In questo caso l'unione coincide con lo spazio degli esiti
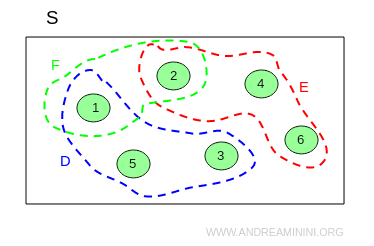
L'intersezione degli eventi E⋂F è un insieme formato dagli esiti presenti sia in E che in F.
$$ E \cap F = \{ 2,4,6 \} \cap \{ 1,2 \} = \{ 2 \} $$
Vista graficamente
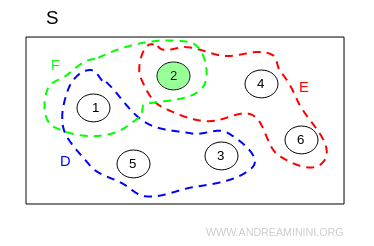
L'intersezione vuota di due eventi vuol dire che i due eventi non possono verificarsi contemporaneamente e sono detti eventi disgiunti o eventi mutamente esclusivi.
$$ E \cap D = \{ 2,4,6 \} \cap \{ 1,3,5 \} = \{ \} $$
Complementare di un evento
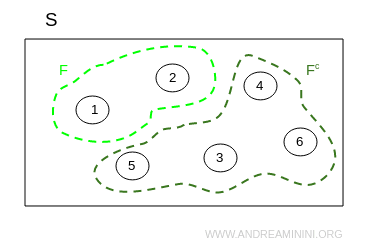
Il complementare Fc di un evento F è l'insieme formato dagli esiti che non verificano F.
Esempio
Se l'evento F è l'insieme dei numeri inferiori a tre ottenuti lanciando un dado
$$ F = \{ 1, 2 \} $$
il suo complementare è l'insieme dei numeri di un dado superiori a due.
$$ F^c = \{ 3, 4, 5, 6 \} $$
In un diagramma di Venn
E così via.
