Evento contrario

Nel campo della probabilità e della statistica, un evento contrario E' rappresenta la circostanza opposta di un determinato evento E.

Se E è un particolare evento, il suo evento contrario (o evento complemento) si indica con il simbolo \(E'\) o \(E^{c}\) e si verifica quando e solo quando non si verifica \(E\).

Ad esempio, se considero il lancio di un dado a sei facce e l'evento \(E\) è "uscita di un numero pari", allora l'evento contrario \(E'\) sarà "uscita di un numero dispari".

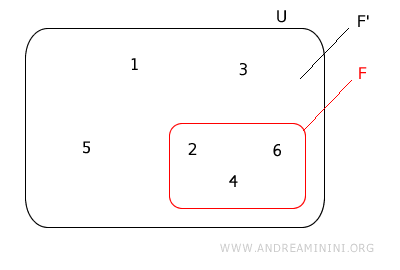
Dal punto di vista della teoria degli insiemi, se U è l'insieme universo che contiene tutto ed F è l'insieme dei casi favorevoli all'evento E, allora F' è l'insieme complementare U\F.

$$ F' = U \text{ \ } F $$

Questo significa che F' contiene tutti gli elementi di U che non sono presenti in F.

Ad esempio, questa è la rappresentazione dell'evento E ("uscita di un numero pari") e dell'evento contrario E' tramite i diagrammi di Eulero-Venn.

Un teorema fondamentale nella teoria della probabilità afferma che la somma della probabilità di un evento e della probabilità del suo evento contrario è sempre uguale a 1 $$ p(E) + p(E') = 1 $$

Questo teorema è molto utile perché mi fornisce un metodo diretto per calcolare la probabilità di un evento conoscendo la probabilità del suo evento contrario.

Dimostrazione. Parto dalla somma delle probabilità dell'evento E e dell'evento contrario E' $$ p(E)+p(E') $$ La probabilità p(E)=f/n è il rapporto tra i casi favorevoli (f) e quelli totali (n). $$ p(E)+p(E') = \frac{f}{n} + p(E') $$ La probabilità p(E')=(n-f)/n dell'evento contrario è il rapporto tra i casi non favorevoli (n-f) e quelli totali (n) $$ p(E)+p(E') = \frac{f}{n} + \frac{n-f}{n} $$ Dopo qualche passaggio algebrico ottengo il rapporto n/n ossia 1. $$ p(E)+p(E') = \frac{f+n-f}{n} = \frac{n}{n} = 1 $$

Un esempio pratico

Considero l'evento E="esce un numero maggiore di 2" dal lancio di un dado a sei facce.

Lo spazio degli eventi è

$$ U = \{ 1,2,3,4,5,6 \} $$

Lo spazio degli eventi favorevoli è il seguente:

$$ F = \{ 3,4,5,6 \} $$

Misuro il quoziente tra la cardinalità dell'insieme F rispetto all'insieme U e ottengo la probabilità dell'evento E.

$$ p(E) = \frac{|F|}{|U|} = \frac{4}{6} = 0.66 $$

La cardinalità dell'insieme F è |F|=4 perché ha 4 elementi mentre quella dell'insieme U è |U|=6.

Quindi, la probabilità che esca un numero maggiore di 2 (evento E) è circa lo 0.67 ossia il 67%.

L'evento contrario E' è lil caso opposto ossia "esce un numero minore o uguale a 2".

In questo caso posso evitare di calcolare la probabilità dell'evento E', poiché conosco già la probabilità p(E)=0.67 dell'evento E posso ottenere quella dell'evento E' per differenza

Sapendo che per il teorema della probabilità la somma delle probabilità di un evento E e dell'evento contrario E' è uguale a 1

$$ p(E) + p(E') = 1 $$

Ricavo la probabilità p(E') in funzione di tutto il resto.

$$ p(E') = 1 - p(E) $$

$$ p(E') = 1 - 0.67 $$

$$ p(E') = 0.33 $$

Ho così ottenuto la probabilità dell'evento E' per differenza e senza doverla calcolare come rapporto tra casi favorevoli e totali.

La probabilità che esca un numero minore o uguale a 2 è circa lo 0.33 ossia il 33%.

E così via.