Teorema della somma delle probabilità di eventi compatibili

Il teorema della somma per eventi compatibili afferma che la probabilità p(E1∪E2) che si verifichi almeno uno tra due eventi compatibili è pari alla somma delle probabilità di ciascun evento, considerato singolarmente, meno la probabilità che entrambi gli eventi si verifichino contemporaneamente. $$ p(E1∪E2) = p(E1)+p(E2)−p(E1∩E2) $$

Dove

• p(E1) è la probabilità che si verifichi l'evento E1
• p(E2) è la probabilità che si verifichi l'evento E2
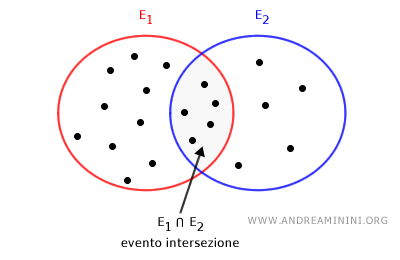
• p(E1​∩E2​) è la probabilità dell'intersezione degli eventi, ossia la probabilità che entrambi gli eventi si verifichino simultaneamente.

Questo teorema fornisce un metodo per calcolare la probabilità p(E1∪E2) che almeno uno di due eventi accada (evento unione) quando gli eventi E1 ed E2 possono verificarsi simultaneamente.

Cosa sono gli eventi compatibili?

Due o più eventi sono eventi compatibili (o non mutuamente esclusivi) se possono verificarsi contemporaneamente.

Dimostrazione. La dimostrazione del teorema della somma per eventi compatibili si basa sul fatto che, contando separatamente la probabilità di ciascun evento, l'evento d'intersezione E1∩E2 viene contato due volte, perché gli elementi in comune sono presenti sia in p(E1) che in p(E2). Dunque, per evitare questa duplicazione, si sottrae la probabilità dell'intersezione una volta.

Un esempio pratico

Considero un mazzo di carte composto da 52 carte e due eventi E1 e E2

E1: "esce un asso"

E2: "esce una carta di cuori"

I due eventi sono compatibili in quanto possono verificarsi simultaneamente, come nel caso in cui si pesca l'asso di cuori.

Per calcolare la probabilità che si verifichi almeno un evento utilizzo il teorema della somma degli eventi compatibili.

$$ p(E1∪E2)=p(E1)+p(E2)−p(E1∩E2) $$

Poiché ci sono 4 assi nel mazzo di 52 carte, la probabilità che esca un asso (evento E1) è 4/52

$$ p(E1) = \frac{4}{52} $$

Ci sono 13 carte di cuori nel mazzo di 52 carte, quindi la probabilità che esca una carta di cuori (evento E2) è 13/52

$$ p(E2) = \frac{13}{52} $$

Ora, calcolo la probabilità che esca una carta sia sia un asso che di cuori p(E1∩E2)

Essendoci solo un asso di cuori su 52 carte, la probabilità è 1/52

$$ p(E1∩E2) = \frac{1}{52} $$

Sostituisco le probabilità appena calcolate nel teorema della somma per eventi compatibili.

$$ p(E1∪E2)=p(E1)+p(E2)−p(E1∩E2) $$

$$ p(E1∪E2)= \frac{4}{52} + \frac{13}{52} − \frac{1}{52} $$

$$ p(E1∪E2)= \frac{4+13-1}{52} $$

$$ p(E1∪E2)= \frac{16}{52} $$

che semplificata diventa

$$ p(E1∪E2)= \frac{4}{13} $$

Quindi, la probabilità di pescare una carta che sia o un asso o una carta di cuori è 4/13​ o approssimativamente il 30.77%.

Osservazioni

Alcune osservazioni e note a margine sul teorema della somma degli eventi compatibili

• Il teorema della somma degli eventi compatibili è valido anche per gli eventi incompatibili
  Il teorema della somma si applica sia agli eventi compatibili che a quelli incompatibili, con la differenza che per eventi incompatibili la probabilità dell'evento intersezione è zero p(E1∩E2)=0, perché l'evento intersezione E1∩E2=Ø è un insieme vuoto, in quanto i due eventi non possono verificarsi contemporaneamente. Semplificando la formula al solo addendo delle probabilità individuali degli eventi senza intersezione. $$ p(E1∪E2)=p(E1)+p(E2)−p(E1∩E2) $$ $$ p(E1∪E2)=p(E1)+p(E2)−p(Ø) $$ $$ p(E1∪E2)=p(E1)+p(E2)−0 $$ $$ p(E1∪E2)=p(E1)+p(E2) $$

E così via.