Variabili aleatorie
Una variabile aleatoria (o casuale) X è una variabile che può assumere un valore casuale tratto da uno spazio degli esiti S.
La variabile aleatoria può assumere un valore compreso nello spazio degli esiti.
In altre parole, è una funzione che prende un valore casuale (esito) da un insieme (spazio degli esiti) e lo assegna a una variabile.
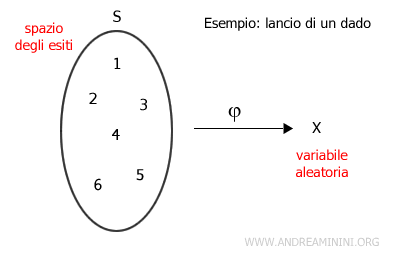
Ogni esito ha una determinata probabilità di verificarsi che può essere uguale o diversa dagli altri.
Gli esiti si escludono a vicenda. Quindi, il verificarsi di un esito esclude quello degli altri.
Esempio. Il lancio di un dado è forse l'esempio più semplice di variabile casuale. Gli esiti sono solo sei S={1,2,3,4,5,6} uno per ogni faccia del dado. E' un fenomeno casuale perché quando lancio il dado non so prevedere quale faccia uscirà. In ogni caso, l'uscita di una faccia (es. 2) esclude quella degli altri numeri, perché un dado può mostrare solo una faccia verso l'alto.
Pertanto, la somma delle probabilità di tutti gli esiti è sempre pari a 1.
L'insieme di tutte le probabilità dello spazio degli eventi è detta distribuzione di probabilità della variabile aleatoria.
A cosa servono le variabili aleatorie
In genere le variabili aleatorie sono usate per indicare l'esito di un esperimento in condizioni di incertezza (fenomeno aleatorio).
Esempio. Posso usare una variabile aleatorie per studiare l'esito del lancio dei dadi oppure di una carta estratta da un mazzo di carte, il moto di un elettrone intorno al nucleo di un atomo, ecc.
Un esempio pratico
Esempio 1
La variabile aleatoria X mostra l'esito del lancio di un dado.
Lo spazio degli esiti S è composto da sei esiti, uno per ogni faccia del dado.
$$ S=\{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \ , \ 5 \ , \ 6 \ \} $$
La variabile aleatoria può assumere uno qualsiasi degli esiti dell'insieme S.

Pertanto, la variabile X può assumere un valore intero da 1 a 6.
Ad esempio X=3 oppure X=5, ecc.
$$ X = \begin{cases} 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \end{cases} $$
Ogni esito ha una determinata probabilità di verificarsi.
Ad esempio, la probabilità che esca X=3 è
$$ p(X=3) = \frac{1}{6} $$
Nota. Per esattezza avrei dovuto scrivere l'esito dell'esperimento tra le parentesi graffe perché si tratta di un elemento di un insieme. $$ p(X=\{ 3 \}) = \frac{1}{6} $$ Tuttavia, spesso per semplificare si usa anche la notazione senza parentesi graffe. $$ p(X=3) = \frac{1}{6} $$
In questo esempio ogni esito ha la stessa probabilità di verificarsi.
Non è detto che sia sempre così.
$$ p(X=1) = \frac{1}{6} \\ p(X=2) = \frac{1}{6} \\ p(X=3) = \frac{1}{6} \\ p(X=4) = \frac{1}{6} \\ p(X=5) = \frac{1}{6} \\ p(X=6) = \frac{1}{6} $$
Poiché la variabile aleatoria può assumere uno di questi valori {1,2,3,4,5,6}, la somma delle probabilità degli esiti è uguale a 1.
$$ p(X=1) + p(X=2) + p(X=3) + p(X=4) + p(X=5) + p(X=6) = $$
$$ = \frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6} = $$
$$ = \frac{6}{6} = 1 $$
In pratica, al 100% deve verificarsi uno degli esiti dell'insieme S= {1,2,3,4,5,6}.
Esempio 2
In questo esempio la variabile aleatoria X è il punteggio ottenuto lanciando due dadi.
Lo spazio degli esiti S è composto da 36 esiti
$$ S = \{ \ (1;1) \ , \ (2;1) \ , \ (3;1) \ , \ ... , \ (6;6) \ \} $$
Nota. La coppia di valori (i;j) indica il punteggio del primo dado (i) e del secondo dado (j) separati da un punto e virgola.
La variabile aleatoria X può assumere un valore intero compreso tra 2 e 12 ottenuto sommando i punteggi dei due dadi.
In questo caso le probabilità di ogni esito sono diverse.
Questa è la distribuzione delle probabilità della variabile aleatoria.
$$ P(X=2) = P(\{(1;1)\}) = \frac{1}{36} $$
$$ P(X=3) = P(\{(2;1),(1;2)\}) = \frac{2}{36} $$
$$ P(X=4) = P(\{(3;1),(1;3),(2;2)\}) = \frac{3}{36} $$
$$ P(X=5) = P(\{(4;1),(1;4),(3;2),(2;3)\}) = \frac{4}{36} $$
$$ P(X=6) = P(\{(5;1),(1;5),(3;3),(4;2),(2;4)\}) = \frac{5}{36} $$
$$ P(X=7) = P(\{(6;1),(1;6),(5;2),(2;5),(4;3),(3;4)\}) = \frac{6}{36} $$
$$ P(X=8) = P(\{(6;2),(2;6),(5;3),(3;5),(4;4)\}) = \frac{5}{36} $$
$$ P(X=9) = P(\{(6;3),(3;6),(5;4),(4;5)\}) = \frac{4}{36} $$
$$ P(X=10) = P(\{(6;4),(4;6),(5;5)\}) = \frac{3}{36} $$
$$ P(X=11) = P(\{(6;5),(5;6)\}) = \frac{2}{36} $$
$$ P(X=12) = P(\{(6;6)\}) = \frac{1}{36} $$
Nota. La probabilità di ottenere un punteggio pari a 7 è molto più alta rispetto a un punteggio pari a 12 oppure a 2.
Anche in questo caso, poiché la variabile aleatoria può assumere un esito tra 2 e 12, la somma delle probabilità degli esiti è uguale a 1.
$$ p(\cup^{12}_{i=2} \ X=i \ ) = 1 $$
La distribuzione della variabile aleatoria
L'insieme delle probabilità p(X=i) degli eventi/esiti della variabile aleatoria sono detti distribuzione o legge della variabile aleatoria.
In genere le distribuzioni di probabilità di una variabile aleatoria sono rappresentate su un diagramma cartesiano o su un istogramma.
Esempio
La variabile aleatoria X mostra il punteggio ottenuto lanciando due dadi.
Lo spazio degli esiti S è composto da 36 esiti
$$ S = \{ \ (1;1) \ , \ (2;1) \ , \ (3;1) \ , \ ... , \ (6;6) \ \} $$
Nota. Ogni esito è una coppia di valori interi (i,j) che indica il punteggio del primo dado (i) e del secondo dado (j).
Gli eventi possibili dell'esperimento sono 11.
Ogni evento è il punteggio ottenuto sommando i due dadi.
$$ X = \{ 2 \ , \ 3 \ , \ 4 \ , \ 5 \ , \ 6 \ , \ 7 \ , \ 8 \ , \ 9 \ , \ 10 \ , \ 11 \ , \ 12 \} $$
La distribuzione delle probabilità di ogni evento è la seguente
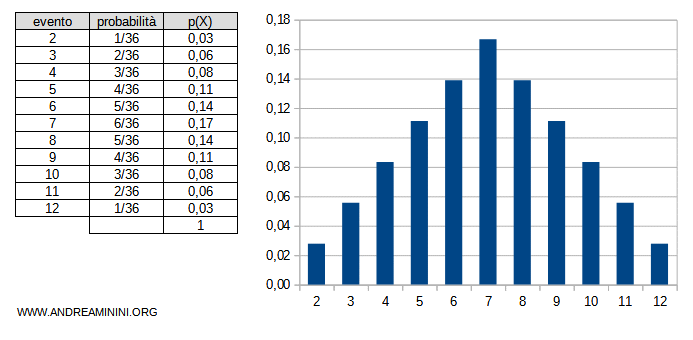
La somma di tutte le probabilità nella distribuzione è pari a 1.
La differenza tra evento ed esito. In genere uso il termine evento per indicare un sottoinsieme di esiti. In questo modo distinguo ogni singolo esito da un gruppo di esiti. Ad esempio, il lancio di due dadi 36 esiti possibili S={(1;2),(2;1),...,(6;6)}. L'evento X è il punteggio ottenuto sommando i due dadi. L'evento X=2 si ottiene solo quando si verifica l'esito (1;1). Quindi la probabilità dell'evento è P(X)=1/36=0,03. L'evento X=3 si ottiene quando si verificano uno di questi due esiti (1;2) oppure (2;1). Quindi la probabilità p(X=2) =2/36=0,06 è il rapporto tra due esiti su trentasei. E via dicendo.
Tipi di variabili aleatorie
Le variabili aleatorie possono essere
- Variabili aleatorie discrete
se lo spazio degli esiti è composto da un numero finito di valori possibili - Variabili aleatorie continue
se lo spazio degli esiti è composto da un numero infinito di valori possibili
Nota. Nel caso delle variabili aleatorie discrete la funzione p(X=k) che associa una probabilità a ogni valore possibili di X è detta funzione di massa di probabilità. Nel caso delle variabili aleatorie continue, la funzione p(a<X<b) che associa una probabilità a ogni intervallo (a;b) di valori di X è detta funzione di densità di probabilità.
Esempio 1
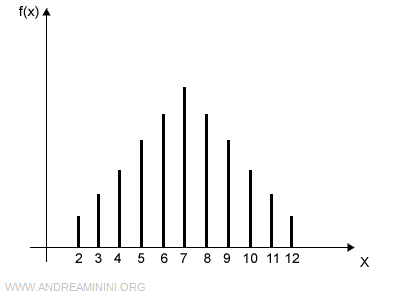
Una variabile aleatoria discreta può assumere un numero finito di valori.
Ad esempio, il punteggio ottenuto lanciando due dadi.
La funzione che associa la probabilità a ogni evento è detta funzione di massa di probabilità.
Esempio 2
Una variabile aleatoria continua può assumere infiniti valori reali.
La sua distribuzione delle probabilità è una funzione continua f(x).
La funzione che associa la probabilità a ogni intervallo (a;b) è detta funzione di densità di probabilità.
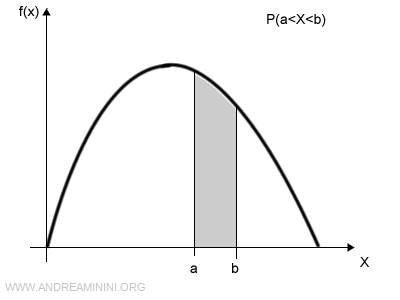
La funzione di densità di probabilità coincide con l'integrale della funzione negli intervallo (a;b)
$$ P(a<X<b) = \int_a^b f(x) \ dx $$
Poiché la variabile aleatoria può assumere uno qualsiasi dei valori dell'insieme infinito, se considero l'intervallo di tutti i numeri reali (-∞,∞) l'integrale della funzione di densità è uguale a 1.
$$ P(-\infty<X<\infty) = \int_{-\infty}^{+\infty} f(x) \ dx = 1 $$
Viceversa, se considero un singolo valore reale (k) l'integrale è uguale alla probabilità p(X=k) che la variabile aleatoria X assuma il valore k.
$$ P(X=k) = \int_{k}^{k} f(x) \ dx $$
La funzione di ripartizione
La funzione di ripartizione si usa per indicare la probabilità che la varabile aleatoria assuma un valore maggiore (o minore) di un determinato valore di soglia k. $$ F(X) = p(X<k) $$
Per indicare che F è una funzione di ripartizione di X si scrive
$$ X \sim F $$
Esempio
La probabilità che il lancio del dado mostri un valore minore di 4.
$$ F(X)=p(X<4) $$
Questo si realizza quando si verifica uno dei seguenti esiti: 1, 2 o 3.
$$ F(X)=p(X<4)=p(X=1)+p(X=2)+p(X=3) $$
$$ F(X)=p(X<4)=\frac{1}{6}+\frac{1}{6}+\frac{1}{6} $$
$$ F(X)=p(X<4)=\frac{3}{6} $$
$$ F(X)=p(X<4)=\frac{1}{2} $$
Quindi, in questo esempio la funzione di ripartizione ha una probabilità del 50%.
E così via.
