La statistica
La statistica è la scienza per apprendere dai dati. Si occupa della raccolta, descrizione, sintesi e analisi dei dati.
L'analisi statistica è un supporto a qualsiasi attività decisionale.
La statistica è suddivisa in due branche:
- Statistica descrittiva
La statistica descrittiva si occupa di raccogliere, descrivere, illustrare e sintetizzare i dati. Si concentra sulla descrizione dei dati raccolti. - Statistica induttiva (o Inferenza statistica)
L'inferenza statistica studia le caratteristiche di una popolazione in regime di incertezza tramite l'osservazione di un campione rappresentativo e il calcolo delle probabilità. Si occupa di trarre conclusioni sulla popolazione.
Calcolo delle probabilità
E' il campo della statistica che studia i fenomeni aleatori e la gestione dell'incertezza.
Perché si chiama statistica
Il termine statistica deriva da "stato" perché i primi tentativi di raccolta dei dati vennero fatti dagli Stati nel XV-XVI secolo.
In particolar modo dalla Chiesa che annotava nelle parrocchie le nascite, i matrimoni e i morti.
Le registrazioni censuarie delle parrocchie erano particolarmente utili per l'amministrazione e il governo degli Stati.
Esempio. Tramite l'aggregazione delle registrazioni censuarie delle parrocchie era possibile estrapolare informazioni utili per organizzare la raccolta dei tributi e gli eserciti, per valutare lo stato di salute pubblica, il rischio di carestie alimentari o epidemiologiche ecc.
Inizialmente il ruolo della statistica era meramente descrittivo dello stato di una popolazione di persone in un determinato momento storico.
A partire dal XIX secolo la statistica divenne una scienza di analisi dei dati in senso più astratto con applicazioni multidisciplinari in ogni campo del sapere (scientifico, sociale, economico).
Le fasi del processo statistico
Il processo statistico è suddiviso in varie fasi:
- La raccolta dei dati
A volte i dati sono già disponibili all'interno di un'organizzazione (Stato, azienda). Altre volte, invece, chi si occupa dell'analisi statistica deve anche organizzare il rilevamento e la raccolta dati ad hoc. - La descrizione
Consiste nell'esporre i dati in modo efficace e facilmente comprensibile. - La sintesi
Consiste nel trovare un dato aggregato sintetico da una moltitudine di dati. - L'analisi
L'analisi statistica si occupa di valutare l'efficacia dei metodi di indagine e di estrarre informazioni utili dai dati statistici.
Nota. Il raggruppamento e la sintesi dei dati comporta la perdita di qualche informazione ma favorisce la leggibilità e l'interpretazione dei dati. Pertanto, il raggruppamento e la sintesi sono due attività fortemente legati all'obiettivo che voglio raggiungere.
La popolazione statistica
Uno dei principali concetti della statistica è il concetto di popolazione.
La popolazione (o universo) è un insieme di oggetti da cui trarre informazioni.
Dove per "oggetto" intendo qualcosa in senso astratto che appartiene a un insieme detto "popolazione".
Può trattarsi di un insieme di oggetti veri e propri (es. bulloni prodotti da una fabbrica) ma anche di un insieme di persone ossia di un "gruppo".
Ogni singolo oggetto della popolazione è detto unità statistica.
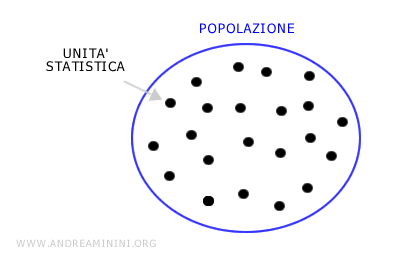
Le unità della popolazione possono essere rappresentate da diversi caratteri.
Esempio. Sono caratteri della popolazione l'altezza, il peso, i colori dei capelli, la cilindrata delle automobili, ecc.
Ogni carattere può essere descritto tramite le modalità.
In base alle modalità i caratteri possono essere di due tipi
- Caratteri qualitativi
I caratteri sono qualitativi se le modalità sono attributi e grandezze non misurabili tramite dei numeri.Esempio. Il colore dei capelli di una persona possono essere neri, biondi, castani, rossi, ecc. I colore è un carattere non misurabile tramite numeri. Il sesso (maschio, femmina) è un altro carattere qualitativo.
- Caratteri quantitativi
I caratteri sono quantitativi se le modalità sono grandezze misurabili tramite dei numeri.Esempio. La modalità dell'altezza è la misura dell'altezza (es. 175 cm, 176 cm, ecc.)
Tipologie di analisi statistiche
L'analisi statistica della popolazione può essere condotta in due modi:
- Censimento
L'analisi viene effettuata su tutti gli oggetti della popolazione. In questo caso si parla di censimento. - Analisi campionaria.
L'analisi viene effettuata soltanto su un sottoinsieme della popolazione detto campione.
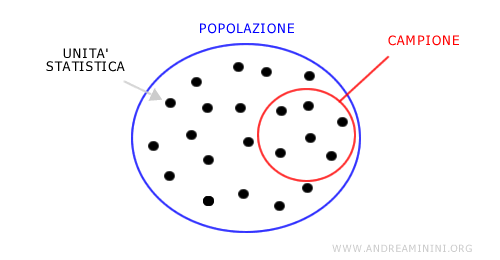
L'analisi campionaria ha essenzialmente due vantaggi: costa meno ed è più rapida.
Tuttavia, per essere efficace, il campione deve essere rappresentativo della popolazione e contenere le stesse informazioni.
Esempio. In una città abitano 100mila persone di ogni età. Organizzo un sondaggio su un campione di 1000 persone. Il campione deve essere rappresentativo della popolazione, ossia deve essere organizzato in modo tale da avere la stessa struttura per età, classe di reddito, titolo di studio, ecc. Se il campione non fosse rappresentativo, l'analisi sul campione rappresenterebbe soltanto delle 1000 persone intervistate ma non anche delle restanti 99mila.
Purtroppo, trovare un campione rappresentativo non è sempre facile.
Spesso i criteri di selezione del campione sono errati o soggettivi e non producono campioni rappresentativi.
Talvolta la scelta di un campione casuale è la via preferibile.
E così via.
