La radice quadrata di un numero reale al quadrato

La radice quadrata di un numero reale $ x $ al quadrato è uguale al valore assoluto del numero stesso $ | x | $. $$ \sqrt{x^2} = |x| $$

La radice quadrata di un numero \( y \) è il numero che, moltiplicato per se stesso, dà \( y \).

Per esempio, la radice quadrata di 9 è 3 perché \( 3 \times 3 = 9 \).

Tuttavia, poiché anche \( (-3) \times (-3) = 9 \), la radice quadrata di 9 potrebbe essere considerata anche \(-3\).

Ma, per convenzione la radice quadrata principale di un numero non negativo è sempre il valore positivo.

Quindi, \( \sqrt{9} = 3 \).

Quando si eleva un numero \( x \) al quadrato, si moltiplica quel numero per se stesso: \( x^2 = x \times x \).

Il quadrato di un numero reale è sempre non negativo, indipendentemente dal segno di \( x \).

Ad esempio, sia per \( x = 3 \) che per \( x = -3 \), ottengo \( x^2 = 9 \).

Ora, se prendo il quadrato di un numero reale \( x \) e poi calcolo la sua radice quadrata, ottengo:

$$ \sqrt{x^2} $$

Dato che il quadrato di \( x \) è sempre non negativo, la radice quadrata di \( x^2 \) sarà il numero positivo che, moltiplicato per se stesso, restituisce \( x^2 \).

Questo numero positivo è esattamente il valore assoluto di \( x \), indicato con \( |x| \).

$$ \sqrt{x^2} = |x| $$

Il valore assoluto di un numero \( x \) è definito come:

$$ |x| =
\begin{cases}
x & \text{se } x \geq 0 \\ \\
-x & \text{se } x < 0
\end{cases} $$

Quindi:

• Se \( x \) è positivo o zero, \( |x| = x \).
• Se \( x \) è negativo, \( |x| \) è il corrispondente positivo di \( x \), cioè il numero senza il segno meno.

In conclusione, per qualunque numero reale \( x \), la radice quadrata del suo quadrato è sempre uguale al valore assoluto di \( x \):

$$ \sqrt{x^2} = |x| $$

Questo avviene perché, indipendentemente dal segno di \( x \), il valore assoluto rappresenta la "distanza" di \( x \) dallo zero sulla retta dei numeri, e la radice quadrata del quadrato di \( x \) deve dare questa distanza, ovvero \( |x| \).

Esempio

La radice quadrata del quadrato di -1 è uguale al valore assoluto di -1.

$$ \sqrt{(-1)^2} = |-1| $$

Il quadrato di -1 è uguale a 1

$$ \sqrt{1} = |-1| $$

Poiché il radicando è un valore positivo, per convenzione la radice è un numero positivo ossia $ sqrt{1} = 1.

$$ 1 = |-1| $$

Il valore assoluto di -1 è lo stesso numero con segno positivo ossia $ |1|=1 $

$$ 1 = 1 $$

Questo dimostra che la radice quadrata di qualsiasi numero reale elevato al quadrato, indipendentemente dal segno, è uguale al valore assoluto del numero stesso.

Note

Alcune note a margine su questo argomento

• La relazione $ \sqrt{x^2} = |x| $ non vale per i numeri complessi
  La relazione $ \sqrt{x^2} = |x| $ vale per tutti i numeri reali, indipendentemente dal segno, ma non vale per i numeri complessi.

  Esempio. Considero la radice quadrata dell'unità immaginaria (i) elevata al quadrato $$ \sqrt{i^2} = |i| $$ Il modulo di qualsiasi numero complesso $ a+ib $ è uguale a $ |a+ib|=\sqrt{a^2+b^2} $. Quindi, il modulo di $ |i|=|0+ i \cdot 1|= \sqrt{0^2+1^2} = 1 $ $$ \sqrt{i^2} = 1 $$ La radice quadrata di $ i^2 $ è semplicemente $ i $ $$ i = 1 $$ Questo però non è possibile perché $ i $ non è uguale al numero reale 1 ma al numero complesso $ i = 0+i \cdot 1 $ dove 0 è la parte reale ed è nulla mentre $ 1 \cdot i $ è la parte immaginaria. In altre parole, l'unità immaginaria $ i $ è il punto (0,1) sul piano di Gauss mentre il numero reale 1 corrisponde al punto (1,0). Sono due punti diversi e a ogni punto del piano di Gauss corrisponde uno e un solo numero complesso. Questo dimostra che la proprietà $ \sqrt{x^2} = |x| $ non è valida per i numeri complessi.
  
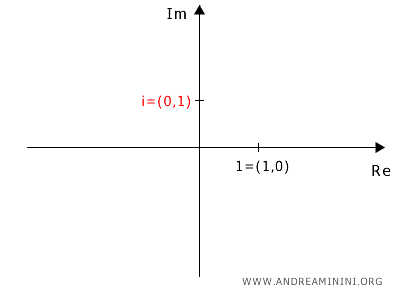
  Una formula valida per i numeri complessi è la seguente: la radice quadrata del prodotto tra un numero complesso $ z $ e il suo coniugato $ \overline{z} $ è uguale al valore assoluto di $ z $ $$ \sqrt{z \cdot \overline{z}} = |z| $$ Ad esempio, se $ z=i $ allora $ \overline{z}=-i $ quindi $$ \sqrt{i \cdot (-i)} = |i| $$ $$ \sqrt{-i^2} = 1 $$ $$ \sqrt{-1 \cdot i^2} = 1 $$ Sapendo che $ i^2=-1 $ $$ \sqrt{-1 \cdot (-1)} = 1 $$ $$ \sqrt{1} = 1 $$ $$ 1=1 $$ Poiché i numeri complessi includono anche i numeri reali, questa formula vale anche per i reali. I numeri reali sono numeri complessi con la parte immaginaria nulla (es. $ z = a+i \cdot 0 $ ). Sapendo che il coniugato di $ z = a+i \cdot 0 $ è  sempre $ \overline{z} = a+i \cdot 0 $, ovvero $ z = a $ e $ \overline{z} = a $, la formula $ \sqrt{z \cdot \overline{z}} = |z| $ torna a essere quella iniziale che è valida solo per i numeri reali. $$ \sqrt{z \cdot \overline{z} } = \sqrt{a \cdot a} = \sqrt{a^2} = |a| $$

E così via.