I radicali simili
- Due radicali sono detti radicali simili se
- sono radicali irriducibili
- hanno lo stesso indice di radice (n)
- hanno lo stesso radicando (m)
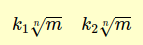
I radicali simili possono avere o meno un diverso coefficiente del radicale (k1 e k2) ossia un fattore che li moltiplica.
Spesso due radicali possono diventare simili portando dentro o fuori dalla radice alcuni fattori.
Nota. I radicali simili sono molto utili perché possono essere sommati tra loro. Ad esempio $$ k_1 \sqrt[n]{m} + k_2 \sqrt[n]{m} = ( k_1 + k_2 ) \cdot \sqrt[n]{m} $$
Un esempio pratico
Considero due radicali
$$ 4 \sqrt[3]{2} $$
$$ 5 \sqrt[3]{2} $$
Sono due radicali simili perché sono radicali irriducibili, hanno lo stesso indice di radicale e lo stesso radicando.
Esempio 2
Questo due radicali non sono simili
$$ 4 \sqrt[4]{2} $$
$$ 5 \sqrt[3]{2} $$
perché hanno un indice di radice differente
Esempio 3
Questi due radicali non sono simili perché hanno un radicando diverso
$$ 2 \sqrt[3]{16} $$
$$ 5 \sqrt[3]{2} $$
Tuttavia, il primo radicando posso trasformarlo spostando alcuni fattori fuori dalla radice
$$ 2 \sqrt[3]{16} $$
$$ 2 \sqrt[3]{2^4} $$
$$ 2 \sqrt[3]{2^3 \cdot 2} $$
$$ 2 \cdot 2 \sqrt[3]{2} $$
$$ 4 \sqrt[3]{2} $$
In questo modo ottengo un radicale equivalente.
$$ 4 \sqrt[3]{2} $$
$$ 5 \sqrt[3]{2} $$
Ora i due radicali sono radicali simili perché hanno lo stesso indice di radice e lo stesso radicando.
E così via.
