Radicali

La radice n-esima è l'operazione inversa della potenza con esponente n.

L'estrazione della radice n-esima di un numero reale a consiste nel determinare un numero reale b tale che la sua potenza n-esima bⁿ sia uguale ad a con n>0.

Il termine a è un numero reale detto radicando mentre n è detto indice della radice. La scrittura ⁿ√a è invece detta radicale.

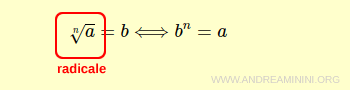
L'indice della radice è un numero naturale diverso da zero n ∈ N-{0}

• Se l'indice della radice è n=2 la radice è detta radice quadrata. Sono anche detti radicali quadratici. $$ \sqrt[2]{a}=b \Longleftrightarrow b^2 = a $$

  Nel caso delle radici quadrate l'indice della radice si omette $$ \sqrt{a}=b \Longleftrightarrow b^2 = a $$

• Se l'indice della radice è n=3 la radice è detta radice cubica. Sono anche detti radicali cubici. $$ \sqrt[3]{a}=b \Longleftrightarrow b^3 = a $$

Dall'indice n=4 in poi la radice è semplicemente detta radice quarta (n=4), radice quinta (n=5), radice sesta(n=6) e via dicendo.

La radice di un numero reale

Se considero un numero reale a∈R qualsiasi e un numero naturale n≠0 diverso da zero

• Se l'indice della radice (n) è dispari ogni numero reale a∈R ha una sola radice n-esima con lo stesso segno algebrico del radicando.
  

  Esempio. La radice cubica di 8 è uguale a 2 perché due elevato alla terza è uguale a otto. $$ \sqrt[3]{8} = 2 \Longleftrightarrow \ 2^3 = 2 \cdot 2 \cdot 2 = 8 $$

• Se l'indice della radice (n) è pari bisogna distinguere tra tre casi
  
  • a>0
    se il radicando è positivo (a>0) esistono due possibili soluzioni con segno algebrico opposto
    
    Tuttavia, per convenzione la radice quadrata di un numero reale è sempre la soluzione positiva $$ \sqrt[n]{a} = b \ \ \ \text{dove} \ \ b>0 $$ Questa scelta permette di attribuire un significato univoco al simbolo \(\sqrt{a}\).

    Esempio. La radice quadrata di 9 è uguale a +3 e non -3. $$ \sqrt{9} = +3 \ \Longleftrightarrow \ 3^2 = 3 \cdot 3 = 9 $$ Tuttavia, quando risolvo un'equazione quadratica come \(x^2 = 9\), devo considerare entrambe le soluzioni, positiva e negativa. Infatti: $$ x^2 = 9 \implies x = \pm \sqrt{9} $$ In questo caso, le soluzioni sono:  $$ \pm \sqrt{9} = \begin{cases} +3 \ \Longleftrightarrow \ 3^2 = 3 \cdot 3 = 9 \\ \\ -3 \ \Longleftrightarrow \ (-3)^2 = (-3) \cdot (-3) = 9 \end{cases} $$ La confusione nasce dall'equazione \(x^2 = a\), che ha due soluzioni: \(x = \pm \sqrt{a}\). In questo caso sono specificate dal simbolo $ \pm $ che precede la radice. In ogni caso \(\sqrt{a}\) è un simbolo che indica specificamente solo la soluzione positiva (o nulla, se il radicando è \(a = 0\)).

  • a=0
    se il radicando è nullo (a=0) esiste una sola radice n-esima di zero ed è sempre uguale a zero.
    

    Nota. La radice n-esima di zero (a=0) esiste ed è sempre uguale a zero perché la potenza ennesima di zero è sempre zero. $$ 0^1 = 0 \\ 0^2 = 0 \cdot 0 = 0 \\ 0^3 = 0 \cdot 0 \cdot 0 = 0 \\ \vdots $$

  • a<0
    se il radicando è negativo (a<0) l'estrazione della radice con indice pari è invece impossibile perché nessun numero reale negativo moltiplicato per se stesso un numero pari di volte ha segno algebrico negativo.
    
    

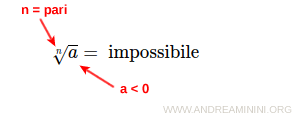
    Cosa fare se il radicando è negativo? E' un errore comune pensare che la radice n-esima di un numero reale sia sempre un'operazione impossibile se il radicando è negativo. In realtà non è così. L'estrazione della radice n-esima di un numero negativo è possibile quando l'indice della radice è dispari. Ad esempio $$ \sqrt[3]{-8}=-2 \Longleftrightarrow (-2)^3 = (-2) \cdot (-2) \cdot (-2) = -8 $$ E' impossibile soltanto se l'indice della radice è pari $$ \sqrt[2]{-8} = \ \text{impossibile} $$

Pertanto, nei radicali è necessario aggiungere una condizione di esistenza C.E. che cambia a seconda dell'indice della radice.

Esempio

Considero il radicale

$$ \sqrt{x-3} $$

E' una radice quadrata. Quindi, l'indice della radice (2) è pari.

In questo caso il radicando (x-3) non può essere negativo. Pertanto devo aggiungere la condizione di esistenza C.E.

$$ \sqrt{x-3} \ \ \ \ \ C.E. \ \ \forall \ x \ge 3 $$

Spiegazione. Il radicando (x-3) non può essere negativo. Scrivo la disequazione $$ x-3 \ge 0 $$ Esplicito l'incognita x sommando 3 in entrambi i membri della disequazione grazie alla proprietà invariantiva $$ x-3+3 \ge 0 +3 $$ $$ x \ge 3 $$ Il risultato finale è la condizione di esistenza C.E. del radicale.

Esempio 2

Ora considero il radicale

$$ \sqrt[3]{x-3} $$

E' una radice cubica. Quindi, l'indice della radice (3) è dispari.

In questo caso il radicando (x-3) può anche essere negativo. Pertanto, la condizione di esistenza ammette qualsiasi valore reale dell'incognita x.

$$ \sqrt{x-3} \ \ \ \ \ C.E. \ \ \forall \ x \in R $$

Nota. Spesso si omette la condizione di esistenza nei radicali con indice dispari. Tuttavia, il mio consiglio è di aggiungere sempre la condizione di esistenza C.E. quando si lavora sui radicali. Anche quando non serve.

Le proprietà e le operazioni dei radicali

Le principali proprietà e operazioni dei radicali

• La potenza m-esima di un radicale
  La potenza m-esima di un radicale è un radicale con lo stesso indice n e con il radicando elevato a m. $$ ( \sqrt[n]{a} )^m = \sqrt[n]{a^m} $$
• La proprietà invariantiva dei radicali
  Il risultato del radicale non cambia se si moltiplica o si divide l'indice della radice e l'esponente del radicando per uno stesso numero positivo. $$ \sqrt[n]{a^m} = \sqrt[n \cdot p]{a^{m \cdot p }} = \sqrt[ \frac{n}{p} ]{a^{ \frac{n}{p} }} $$
• Il prodotto dei radicali con lo stesso indice
  Il prodotto di due radicali con lo stesso indice (n) è un radicale che ha sempre lo stesso indice n e per radicando il prodotto dei radicandi $$ \sqrt[n]{a^m} \cdot \sqrt[n]{b^p} = \sqrt[n]{a^m \cdot b^p } $$

  Nota. Se i radicali non hanno lo stesso indice, per fare la moltiplicazione devo prima ridurli al minimo comune indice.

• Il quoziente dei radicali con lo stesso indice
  Il quoziente di due radicali con lo stesso indice (n) è un radicale che ha sempre lo stesso indice n e per radicando il quoziente dei radicandi $$ \frac{ \sqrt[n]{a^m} }{ \sqrt[n]{b^p} } = \sqrt[n]{ \frac{a^m}{ b^p } } $$
• La radice di un radicale
  La radice di un radicale è un radicale che ha per indice il prodotto degli indici e per radicando lo stesso radicando. $$ \sqrt[n]{ \sqrt[p]{a} } = \sqrt[n \cdot p]{a} $$

  Nota. Dalla formula risolutiva della radice di un radicale deriva anche la possibilità di scambiare gli indici di radice tra loro. $$ \sqrt[m]{\sqrt[n]{a}} = \sqrt[n]{\sqrt[m]{a}} $$

• Trasporto del fattore fuori dalla radice
  Un fattore del radicando con esponente uguale o maggiore dell'indice della radice m ≥ n può essere portato fuori dalla radice se m=n·q+r. $$ \sqrt[n]{a^m} = \sqrt[n]{a^{n \cdot q + r}} = \sqrt[n]{a^{n \cdot q} \cdot a^r} = \sqrt[n]{a^{n \cdot q}} \cdot \sqrt[n]{a^r} = a^q \cdot \sqrt[n]{a^r} $$

  Esempio. $$ \sqrt[3]{a^5} = \sqrt[3]{ a^{3 \cdot 1 + 2} } = \sqrt[3]{ a^3 \cdot a^2 } = \sqrt[3]{ a^3} \cdot \sqrt[3]{ a^2 } = a \cdot \sqrt[3]{ a^2 } $$

• Trasporto del fattore dentro la radice
  Un fattore esterno al radicale può essere portato dentro la radice elevandolo all'indice della radice. $$ b \cdot \sqrt[n]{a} = \sqrt{b^n \cdot a} $$

  Esempio. $$ a \cdot \sqrt[3]{ a^2 } = \sqrt[3]{a^3 \cdot a^2} $$

Radicali particolari

Alcuni radicali particolari a cui fare attenzione

$$ \sqrt{a^2} = | a | $$

Nota. La radice quadrata del quadrato di un numero reale $ \sqrt{a^2} $ è uguale al valore assoluto del numero reale | a |. Questo è vero perché la radice quadrata di un numero non negativo (come a² per ogni numero reale a) restituisce il valore positivo, che corrisponde al valore assoluto del numero originale |a|. Questa proprietà vale per tutti i numeri reali ma non vale per i numeri complessi. Vedi approfondimento.

$$ (\sqrt[n]{a})^n = a $$

$$ \sqrt[n]{a^m} = a^{\frac{m}{n}} $$

$$ \sqrt[1]{a} = a^1 = a $$

$$ \sqrt[n]{0} = 0^n = 0 $$

$$ \sqrt[n]{1} = 1^n = 1 $$

$$ \sqrt[0]{a} = indefinito $$

$$ \sqrt[pari]{a<0} = indefinito $$

La radice quadrata nei numeri complessi

Nel campo dei numeri reali la radice quadrata di un numero reale non negativo \(a\) è definita per convenzione come la soluzione non negativa dell'equazione \(x^2 = a\).

Ad esempio, \( \sqrt{25} = 5\), non \(\pm 5\), \(\sqrt{0} = 0\), \(\sqrt{4} = 2\), ecc.

Nei numeri complessi, la situazione è diversa perché il concetto di radice quadrata diventa polidromo.

Ogni numero complesso \(z \neq 0\) ha due radici quadrate oppure infinite radici nel caso generale \(z^n = w\), con \(n > 2\).

Per vedere un esempio pratico rimando ai miei appunti sulla radice di un numero complesso.

E così via.