Studio della soluzione di un'equazione differenziale
Lo studio della soluzione y(t) dell'equazione differenziale si effettua quando l'equazione differenziale è un modello che rappresenta un fenomeno fisico reale nel tempo (t) rispetto a una condizione iniziale.
Dove la variabile indipendente è il tempo.
Per studiare la soluzione devo calcolare l'intervallo massimale di esistenza, il tempo di vita e l'eventuale tipo di morte
Intervallo massimale di esistenza
L'intervallo massimale di esistenza è l'insieme in cui è definita la soluzione y(t) che contiene il tempo iniziale.
Esempio
Se la soluzione è
$$ y(t)= \frac{-2}{t^2-1} $$
e la condizione iniziale è y(0)=2
$$ y(0)=2 $$
il dominio della funzione è
$$ (-\infty, -1) \cup (-1 , 1) \cup (1, \infty) $$
In questo caso l'intervallo massimale di esistenza è (-1;1) perché in questo intervallo è contenuto il tempo iniziale.
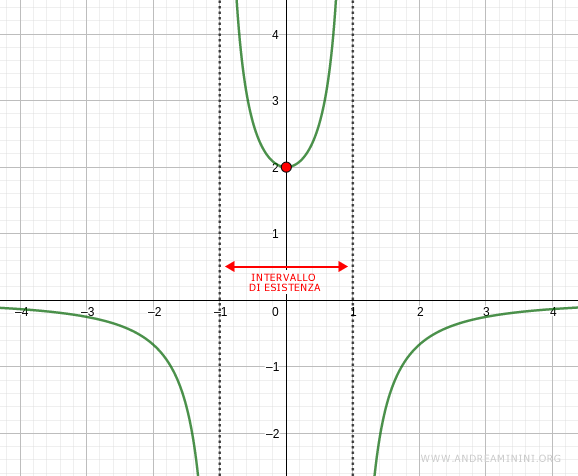
Nell'istante iniziale t=0 la funzione vale y(t)=2
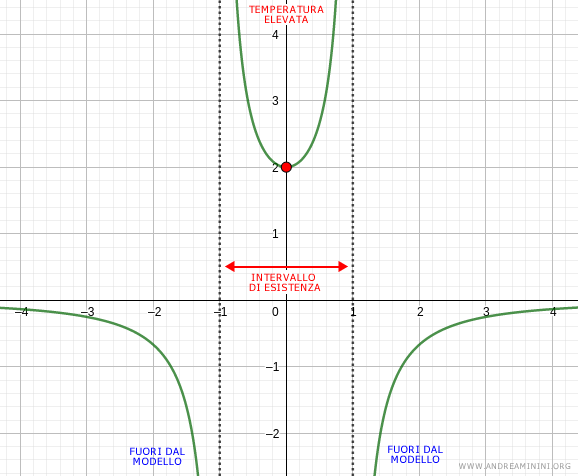
Al di fuori dell'intervallo di esistenza il modello non ha significato.
Esempio. Per t=1 o t=-1 la funzione y(t) tende a infinito. Questo potrebbe voler dire che il calore del circuito è talmente alto da fonderlo. Non ha alcun senso sapere che negli altri due intervalli (-∞;-1) e (1;∞) la temperatura sia infinitamente freddo a sinistra di -1 e a destra di +1, perché sono solo aspetti matematici. Al di fuori dell'intervallo massimale di esistenza (-1;1) si va al di fuori del modello
Tempo di vita nel futuro o nel passato
Il tempo di vita nel futuro e nel passato sono rispettivamente l'estremo superiore e inferiore dell'intervallo di esistenza
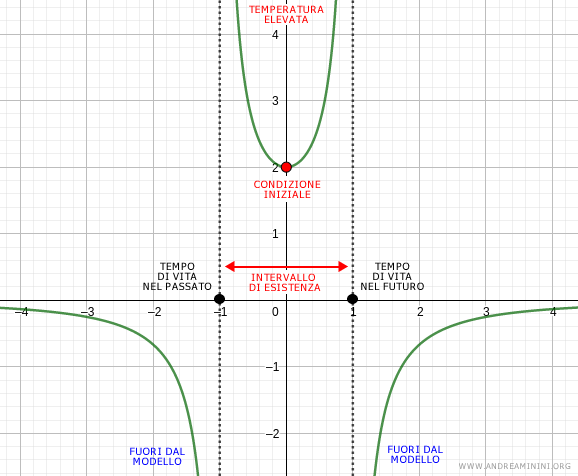
Nota. In questo esempio il tempo di vita nel futuro è 1 mentre il tempo di vita nel passato e -1
E' importante notare che il tempo di vita dipende dalla condizione iniziale.
Quindi, si parla di tempo di vita passato e futuro relativamente alla condizione iniziale.
Tipo di morte
Una volta studiato il tempo di vita studio se il sistema tende a morire oppure no nel corso del tempo.
Se il tempo di vita nel futuro è infinito il sistema non collassa mai, continua a esistere in qualsiasi istante futuro.
Viceversa, se il tempo di vita nel futuro è un numero finito si possono verificare due tipi di morte
- blow up (esplosione)
Si verifica quando il limite della funzione incognita per t che tende al tempo di vita nel futuro è più o meno infinito. Ad esempio, è il caso in cui il circuito si brucia per l'eccessivo calore causato dal prolungato utilizzo nel tempo. - break down
Si verifica quando la soluzione y(t) fa uscire il lato destro dell'equazione differenziale dal campo di definizione.
Esempio
In questo caso il sistema tende a un tipo di morte blow up

In quest'altro caso, invece, il tipo di morte è del tipo break down
In pratica il sistema si rompe, smette di funzionare e di produrre effetti
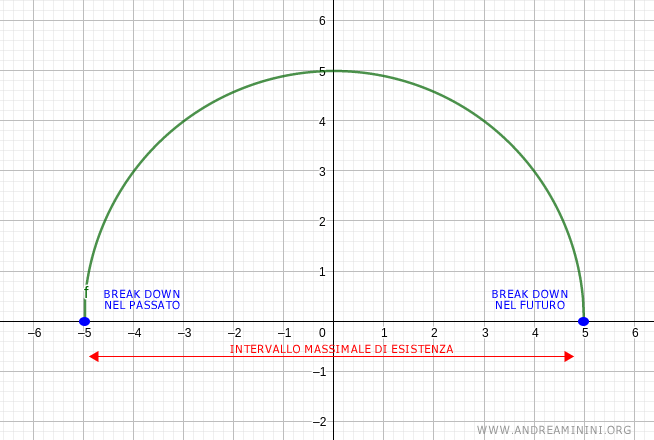
Per un esempio pratico
E così via.
