Problema di Cauchy

Cos'è il problema di Caucy

Il problema di Cauchy è la soluzione particolare di un'equazione differenziale di una funzione y=f(x) in cui la curva integrale passa per un punto assegnato (x₀,y₀). $$ \begin{cases} y'=F(x;y) \\ y_0=f(x_0) \end{cases} $$

La condizione y₀=f(x₀) è detta condizione iniziale del problema di Cauchy.

Per risolvere il problema di Cauchy devo trovare tra le infinite soluzioni dell'equazione differenziale quella che soddisfa la condizione iniziale.

In pratica devo individuare la funzione y=f(x) che soddisfa l'equazione differenziale e passa per il punto (x₀,y₀).

Nota. In un problema di Cauchy può esserci una o più condizioni iniziali. In generale posso dire che il problema di Cauchy per un'equazione differenziale di ordine n è l'equazione differenziale stessa e n condizioni da assegnare in un punto x₀, dove x₀ è un punto dell'intervallo I e y₀,y₁,...,y_n-1 sono le condizioni iniziali assegnate alle funzioni y,y', y'', ... , y_n-1. $$ \begin{cases} y^{(x)}= f(x,y(x),...,y^{(n-1)}(x) \\ y(x_0)=y_0 \\ y'(x_0) = y_1 \\ ... \\ y^{n-1}(x_0) = y_{n-1} \end{cases} $$ Una soluzione y del problema di Cauchy è una funzione y ∈ Cⁿ(I) che soddisfa l'equazione differenziale per ogni x∈I e le n-1 condizioni iniziali. Dove una funzione y appartiene a Cn(I) se è derivabile n volte nell'intervallo I.

Le condizioni iniziali di un'equazione differenziale devono essere tante quanti sono i parametri da determinare.

Inoltre, le condizioni iniziali devono indicare il valore delle funzioni nello stesso punto x₀.

Un esempio pratico

Ecco un esempio di problema di Cauchy

$$ \begin{cases} y'-2x=3 \\ f(2)=3 \end{cases} $$

Quindi la funzione derivata è

$$ y'=3+2x $$

L'integrale generale della funzione y' è

$$ \int{ y' \: dx }= \int{3+2x \:dx} $$

$$ y= 3x+x^2+c $$

Ho così trovato la famiglia delle funzioni y ( soluzione generale ).

$$ y = 3x+x^2+c $$

Devo trovare quella che rispetta le condizioni iniziali y(2)=3 del problema dove x=2 e y=f(x)=3.

Quindi sostituisco le condizioni iniziali alla y.

$$ y = 3x+x^2+c $$

$$ 3 = 3 \cdot 2+2^2+c $$

$$ 3 = 6+4+c $$

$$ 3 = 10 +c $$

Poi trovo la costante c

$$ c = 3-10 = -7 $$

Ho così trovato la soluzione particolare del problema di Cauchy.

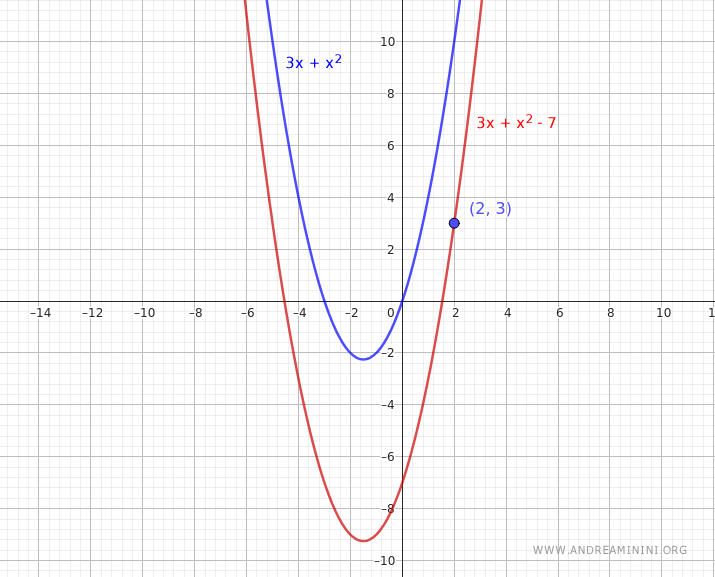
$$ y = 3x+x^2-7 $$

Questa funzione passa effettivamente nel punto alle coordinate (x;y)=(2;3).

Esempio 2

Devo risolvere l'equazione differenziale del primo ordine.

$$ \begin{cases} y'=-e^{-x} \\ y(0)=3 \end{cases} $$

La soluzione generale dell'equazione differenziale è

$$ y' = -e^{-x} $$

$$ \int y' \ dx = \int -e^{-x} \ dx $$

$$ y = e^{-x} +c $$

A questo punto impongo la condizione iniziale y(0)=3 dove x=0 e y=f(x)=3.

$$ 3 = e^{-0} +c $$

$$ 3 = 1 +c $$

Ottengo il valore del parametro c

$$ c = 3 -1 $$

$$ c = 2 $$

Quindi, la soluzione particolare dell'equazione differenziale la ottengo fissando c=2

$$ y = e^{-x} +c $$

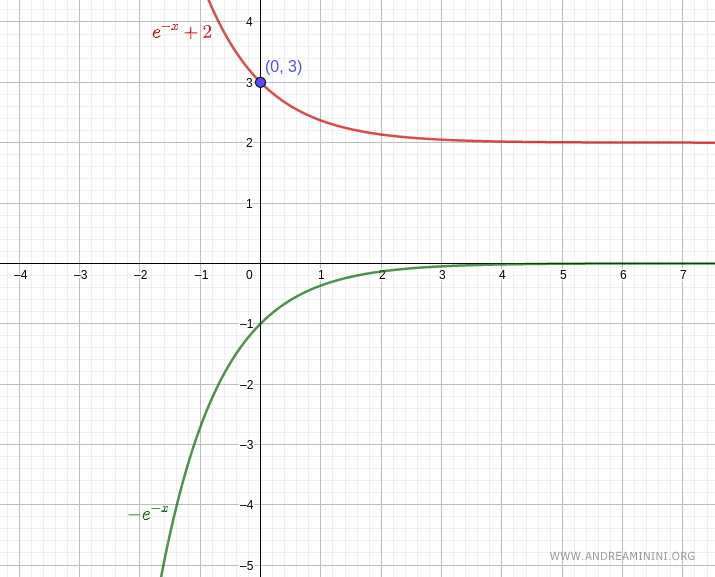
$$ y = e^{-x} +2 $$

La funzione passa per il punto (x,y)=(0,3)

Esempio 3

Devo risolvere l'equazione differenziale del secondo ordine.

$$ \begin{cases} y''=2x \\ y'(1)=2 \\ y(1)=3 \end{cases} $$

In questo caso ci sono due condizioni iniziali, quindi per trovare la soluzione particolare devo trovare due parametri.

Per prima cosa integro la derivata seconda per trovare la funzione y'

$$ y'' = 2x $$

$$ \int y'' \ dx = \int 2x \ dx $$

$$ y' = x^2+c_1 $$

Poi integro la derivata prima y' per trovare la funzione y

$$ y' = x^2+c_1 $$

$$ \int y' = \int x^2+c_1 $$

$$ y = \frac{1}{3} x^3 + c_1 x + c_2 $$

Quest'ultima è la soluzione generale dell'equazione differenziale.

A questo punto impongo la condizione iniziale y'(1)=2 con x=1 nella funzione derivata prima y' per trovare il parametro c₁

$$ y' = x^2+c_1 $$

$$ 2 = 1^2+c_1 $$

$$ c_1 = 2 -1 $$

$$ c_1 = 1 $$

Poi impongo la condizione iniziale y(1)=3 con x=1 nella funzione y=f(x) per trovare il parametro c₂

$$ y = \frac{1}{3} x^3 + c_1 x + c_2 $$

$$ 3 = \frac{1}{3} \cdot 1^3 + c_1 \cdot 1 + c_2 $$

$$ 3 = \frac{1}{3} + c_1 + c_2 $$

Sapendo che c₁=1

$$ 3 = \frac{1}{3} + 1 + c_2 $$

$$ c_2 = 3 - \frac{1}{3} - 1 $$

$$ c_2 = \frac{6-1}{3} $$

$$ c_2 = \frac{5}{3} $$

A questo punto sostituisco i valori ai parametri c₁=1 e c₂=5/3 nella funzione y=f(x)

$$ y = \frac{1}{3} x^3 + c_1 x + c_2 $$

$$ y = \frac{1}{3} x^3 + 1 \cdot x + \frac{5}{3} $$

Il risultato finale è la soluzione particolare dell'equazione differenziale

$$ y = \frac{1}{3} x^3 + x + \frac{5}{3} $$

Quest'ultima funzione rispetta entrambe le condizioni iniziali del problema di Cauchy.

$$ \begin{cases} y''=2x \\ y'(1)=2 \\ y(1)=3 \end{cases} $$

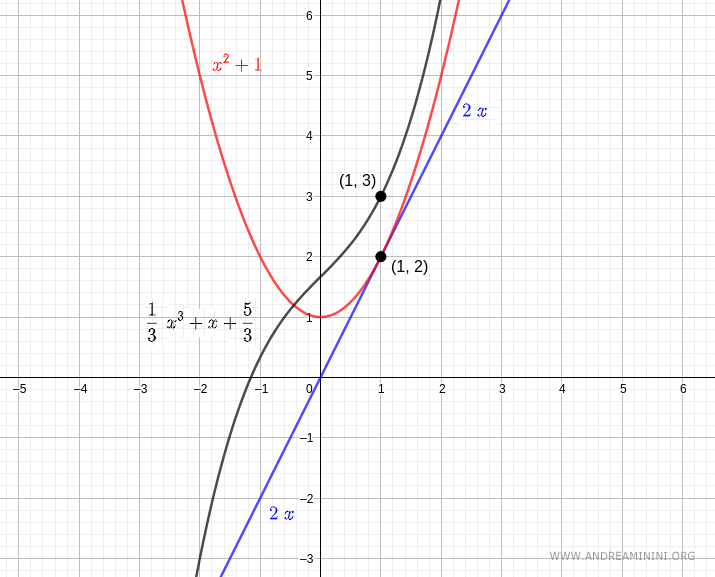
La funzione della derivata prima y'=x²+1 (quella di colore rosso) passa per il punto (1,2).

La funzione y=1/3x³+x+5/3 (quella di colore nero) passa per il punto (1,3)

E così via.