Il metodo di Eulero

Cos'è il metodo di Eulero

Il metodo di Eulero mi permette di trovare una soluzione particolare approssimata di un'equazione differenziale a partire da una condizione iniziale. E' anche detto metodo delle differenze finite.

A cosa serve?

Spesso trovare la soluzione di un'equazione differenziale non è semplice, perché molte equazioni differenziali non sono facilmente integrabili.

In molti problemi pratici mi potrei però accontentare anche di una soluzione approssimata.

Per trovare una soluzione approssimata posso usare uno dei metodi numerici del calcolo numerico. Ad esempio, il metodo di Eulero.

Nota. Il metodo di Eulero ha comunque dei limiti. Può trovare soltanto le soluzioni particolari di un'equazione differenziale. Non la soluzione generale. Inoltre, è necessario imporre una condizione iniziale. Quindi, è particolarmente utile solo per risolvere problemi concreti e reali, dove non occorre conoscere la soluzione generale.

Come funziona il metodo di Eulero

Il metodo si basa sulla sostituzione della derivata prima di una funzione y' con il rapporto incrementale Δy/Δx.

$$ y' \Rightarrow \frac{\Delta y}{\Delta x}$$

Una generica equazione differenziale del primo ordine si presenta in questa forma

$$ y'=f(x,y) $$

Uno dei primi passi da fare è imporre una condizione iniziale.

$$ y_0 = y(x_0) $$

Per trovare la soluzione approssimata dell'equazione differenziale in un particolare punto x*, suddivido l'intervallo (x₀,x*) in n intervalli di pari ampiezza Δx

$$ \Delta x = \frac{x*-x_0}{n} $$

A questo punto calcolo i valori approssimati y_i e l'incremento Δy_i

$$ y_i = f(x_i) $$

$$ \Delta y_i = y_{i+1}-y_i $$

dove il contatore i è un numero intero i=0,1,...,n

Per l'ipotesi iniziale il rapporto incrementale y'=Δy/Δx sostituisce la derivata

$$ \frac{ \Delta y }{ \Delta x } = y' = f(x,y) $$

Quindi

$$ \Delta y = y' \Delta x = f(x,y) \Delta x $$

Questi valori mi permettono di calcolare il valore "stimato" successivo della funzione.

$$ y_{i+1} = y_i + y' \Delta x$$

$$ y_{i+1} = y_i + f(x_i,y_i) \Delta x$$

$$ y_{i+1} = y_i + \Delta y $$

Pertanto, ogni ciclo utilizza l'ultimo valore approssimato della funzione yi per calcolare il valore approssimato successivo yi+1.

Nota. I cicli possono essere ottenuti al computer con un'iterazione oppure con una ricorsione. Se l'intervallo ha molti valori l'uso dell'iterazione permette di usare una minore quantità di memoria rispetto alle ricorsioni.

Ogni ciclo individua un punto (xi,yi) sul piano cartesiano.

L'unione di questi punti con una spezzata genera il grafico approssimato della funzione y(x) nell'intervallo.

Un esempio pratico

In questo esempio considero l'equazione differenziale del primo ordine

$$ y' = y+x $$

Ho scelto appositamente un'equazione differenziale di cui conosco la soluzione, in modo da poter confrontare la soluzione stimata con la soluzione analitica (reale).

Nota. Quando si lavora con i metodi numerici è sempre utili valutare la loro affidabilità tramite dei problemi giocattolo, ossia dei problemi di cui si conosce già la soluzione analitica.

Voglio calcolare la soluzione particolare nel punto x*=1

$$ x* = 1 $$

Considero come condizione iniziale x₀=0 e y₀=1

$$ x_0 = 0 $$

$$ y_0 = y(x_0) = y(0)= 1 $$

Quindi l'intervallo in cui studiare la funzione è (0;1)

$$ (x_0 ; x* ) = ( 0;1) $$

Suddivido l'intervallo in 5 sottointervalli ciascuno di ampiezza Δ=0.2

$$ \Delta x = \frac{x*-x_0}{n} = \frac{1-0}{5} = 0.2 $$

A questo punto inizia l'iterazione

Ciclo 1

Conosco il valore della funzione in x=0

$$ x_0=0 $$

$$ y_0=1 $$

Calcolo l'incremento

$$ \Delta y_1 = f(x_0,y_0) \Delta x $$

$$ \Delta y_1 = f(0, 1) \Delta x $$

Sapendo che f(x)=y+x

$$ \Delta y_1 = (1+0) \Delta x $$

e che Δx=0.2

$$ \Delta y_1 = (1+0) \cdot 0.2 $$

$$ \Delta y_1 = 0.2 $$

Sapendo che il valore successivo della funzione è y₁=y₀+Δy₁

$$ y_1 = y_0 + \Delta y_1 $$

$$ y_1 = 1 + 0.2 $$

$$ y_1 = 1.2 $$

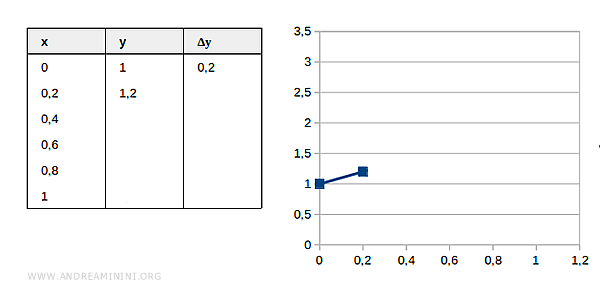
Ciclo 2

Conosco il valore stimato della funzione in x=0.2

$$ x_1= x_0 + \Delta x = 0 + 0.2 = 0.2 $$

$$ y_1=1.2 $$

Calcolo l'incremento

$$ \Delta y_2 = f(x_1,y_1) \Delta x $$

$$ \Delta y_2 = f(0.2, 1.2) \Delta x $$

Sapendo che f(x)=y+x e che Δx=0.2

$$ \Delta y_2 = (0.2+1.2) \cdot 0.2 $$

$$ \Delta y_2 = 0.28 $$

Sapendo che il valore successivo della funzione è y₂=y₁+Δy₂

$$ y_2 = y_1 + \Delta y_2 $$

$$ y_2= 1.2 + 0.28 $$

$$ y_2 = 1.48 $$

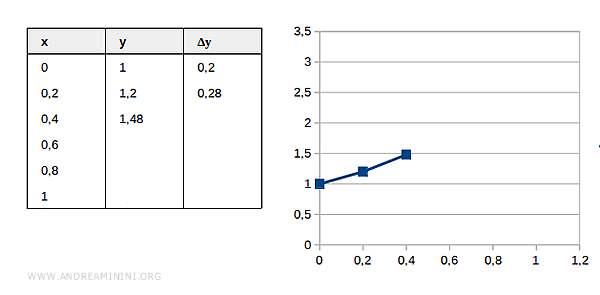
Ciclo 3

Conosco il valore stimato della funzione in x=0.4

$$ x_2= x_1 + \Delta x = 0.2 + 0.2 = 0.4 $$

$$ y_2=1.48 $$

Calcolo l'incremento

$$ \Delta y_3 = f(x_2,y_2) \Delta x $$

$$ \Delta y_3 = f(0.4, 1.48) \Delta x $$

Sapendo che f(x)=y+x e che Δx=0.2

$$ \Delta y_3 = (0.4+1.48) \cdot 0.2 $$

$$ \Delta y_3 = 0.376 $$

Sapendo che il valore successivo della funzione è y₃=y₂+Δy₃

$$ y_3 = y_2 + \Delta y_3 $$

$$ y_3= 1.48 + 0.376 $$

$$ y_3 = 1.856 $$

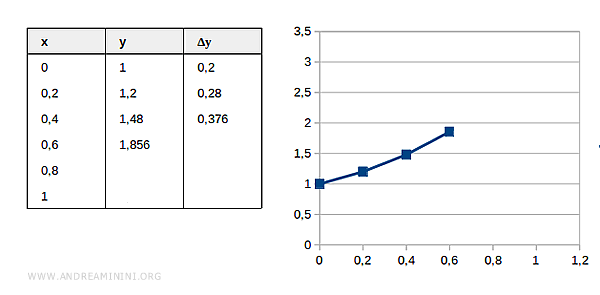
Ciclo 4

Conosco il valore stimato della funzione in x=0.6

$$ x_3= x_2 + \Delta x = 0.4 + 0.2 = 0.6 $$

$$ y_3=1.856 $$

Calcolo l'incremento

$$ \Delta y_4 = f(x_3,y_3) \Delta x $$

$$ \Delta y_4 = f(0.6, 1.856) \Delta x $$

Sapendo che f(x)=y+x e che Δx=0.2

$$ \Delta y_4 = (0.6+1.856) \cdot 0.2 $$

$$ \Delta y_4 = 0.4912 $$

Sapendo che il valore successivo della funzione è y₄=y₃+Δy₄

$$ y_4 = y_3 + \Delta y_4 $$

$$ y_4= 1.856 + 0.4912 $$

$$ y_4 = 2.3472 $$

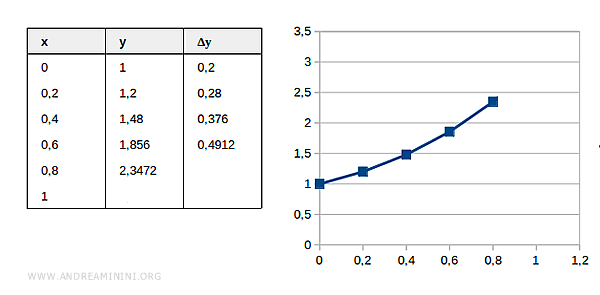
Ciclo 5

Conosco il valore stimato della funzione in x=0.8

$$ x_4= x_3 + \Delta x = 0.6 + 0.2 = 0.8 $$

$$ y_4=2.3472 $$

Calcolo l'incremento

$$ \Delta y_5 = f(x_4,y_4) \Delta x $$

$$ \Delta y_5 = f(0.8, 2.3472) \Delta x $$

Sapendo che f(x)=y+x e che Δx=0.2

$$ \Delta y_5 = (0.8+2.3472) \cdot 0.2 $$

$$ \Delta y_5 = 0.62944 $$

Sapendo che il valore successivo della funzione è y₅=y₄+Δy₅

$$ y_5 = y_4 + \Delta y_5 $$

$$ y_5= 2.3472 + 0.62944 $$

$$ y_5 = 2.97664 $$

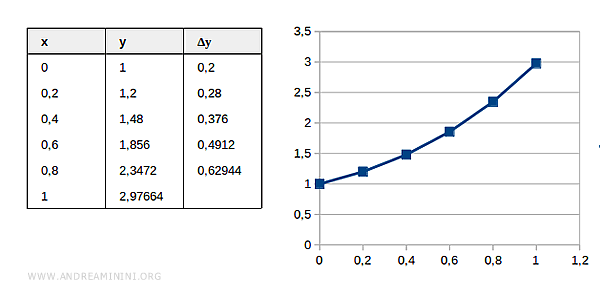
Ciclo 6

Conosco il valore stimato della funzione in x=1.0

$$ x_5= x_4 + \Delta x = 0.8 + 0.2 = 1.0 $$

$$ y_5 = 2.97664 $$

Ho raggiunto il punto x*=1 in cui volevo studiare la soluzione della funzione.

Pertanto, la soluzione approssimata è y(1)=2.97664

$$ y(1) = 2.97664 $$

La spezzata di Eulero approssima la forma della funzione y reale abbastanza bene fino al punto x=1

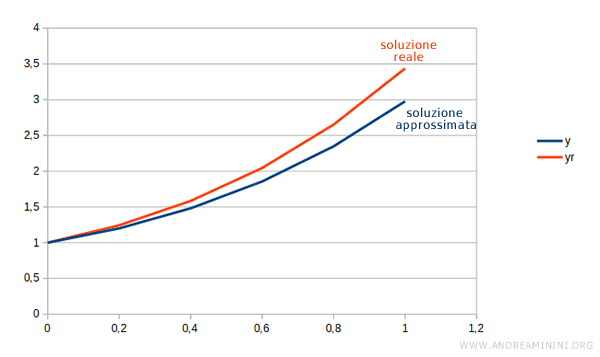
Tuttavia, il margine di errore è ancora molto alto.

Nota. Basti pensare che la funzione reale assume il valore y_R(1)=3.43 nel punto x=1. L'errore assoluto tra il valore stimato e quello reale è $$ E = | 2.97664 - 3.43 | = 0.45 $$ Mentre l'errore relativo è $$ \frac{E}{y_R} = \frac{0.45}{3.43} = 0.131 = 13.1% $$ Un errore del 13% è molto alto.

Come migliorare l'accuratezza della soluzione approssimata?

Per migliorare l'accuratezza della soluzione approssimata posso aumentare il numero di intervalli nella partizione.

Questo mi permette di ridurre l'ampiezza degli intervalli Δx.

Ad esempio, uso una partizione di 20 intervalli

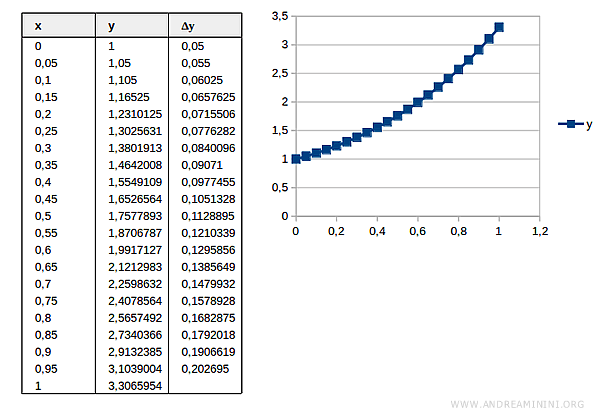
Con una partizione di 20 intervalli la soluzione approssimata è y(1)=3.30

E' molto più vicina alla soluzione reale y_R(1)=3.43

E così via.