La distribuzione di Poisson
La distribuzione poissoniana è una distribuzione di probabilità discreta di tipo esponenziale. $$ P(n) = \frac{λ^n}{n!} e^{-λ} $$
Come funziona
Sapendo che in un intervallo di tempo un evento si verifica λ volte, calcola la distribuzione della probabilità in base al numero di eventi (n) che potrebbero verificarsi.
$$ P(n) = \frac{λ^n}{n!} e^{-λ} $$
Dove
- P(n) è la distribuzione di probabilità su n eventi.
- λ è il numero medio di eventi che si verificano nell'intervallo di tempo.
- e è la base dei logaritmi naturali (e=2,71828)
La formula mi permette di sviluppare in serie la distribuzione della probabilità.
Per n→ ∞ la somma di P(n) è uguale a 1
$$ \sum_{0}^{n} P(n) = 1 $$
Per spiegare meglio come funziona, faccio un esempio pratico.
Un esempio pratico
In un'ora un evento si verifica in media 5 volte
$$ λ=5 $$
Esempio. In un ufficio postale ci sono in media 5 clienti in un'ora.
Voglio calcolare la distribuzione di Poisson delle probabilità che si verifichino n=0,....,8 eventi.
$$ P(0) = \frac{5^0}{0!} e^{-5} = 0.0067 $$ $$ P(1) = \frac{5^1}{1!} e^{-5} = 0.0337 $$ $$ P(2) = \frac{5^2}{2!} e^{-5} = 0.0842 $$ $$ P(3) = \frac{5^3}{3!} e^{-5} = 0.1404 $$ $$ P(4) = \frac{5^4}{4!} e^{-5} = 0.1755 $$ $$ P(5) = \frac{5^5}{5!} e^{-5} = 0.1755 $$ $$ P(6) = \frac{5^6}{6!} e^{-5} = 0.1462 $$ $$ P(7) = \frac{5^7}{7!} e^{-5} = 0.1044 $$ $$ P(8) = \frac{5^8}{8!} e^{-5} = 0.0653 $$
Rappresento graficamente la distribuzione su un diagramma cartesiano
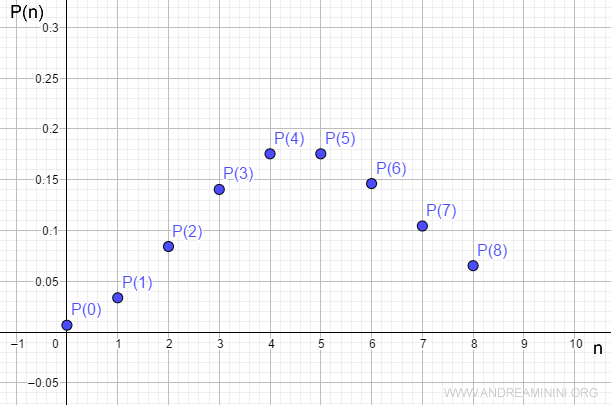
Pertanto, la probabilità che in un'ora non entri nessun cliente è pari a P(0)=0.0067.
La probabilità che entri un solo cliente è P(1)=0.0337
E così via
Nota. Continuando a calcolare la probabilità dell'evento n-esimo, arriverà il punto in cui la probabilità P(n) si annulla. A quel punto la somma delle prime n probabilità è pari a 1. $$ P(1)+(P2)+...+P(n) = 1 $$
