Minimo e massimo locale nelle funzioni con più variabili

In una funzione con due o più variabili, i massimi e i minimi locali possono trovarsi nei

• Punti stazionari. Dove le derivate prime sono nulle: \[ \frac{\partial f}{\partial x} = 0 \quad \text{e} \quad \frac{\partial f}{\partial y} = 0 \] Questi punti sono generalmente i candidati principali.
• Punti singolari. Dove la funzione o le derivate non esistono (tipo buchi, cuspidi, spigoli). Sperando di non trovarli... perché l'analisi della funzione si complica.
• Punti del bordo. Se il dominio è limitato (tipo dentro un cerchio, un quadrato, ecc.), bisogna controllare anche cosa succede sui bordi. Perché magari la funzione ha il massimo o il minimo proprio ai suoi confini.

Nota. Il criterio di ricerca dei punti di minimo e massimo è simile alle funzioni con una variabile. Nelle funzioni di una variabile \( y=f(x) \), i massimi e i minimi si cercano nei punti stazionari, nei punti singolari e agli estremi dell'intervallo \([a,b]\). Nelle funzioni di due variabili \( z=f(x,y) \), si cercano nei punti stazionari, nei punti singolari e sui bordi del dominio, che sono curve chiuse come il bordo di un cerchio.

Secondo il teorema di Weierstrass, se una funzione di due o più variabili è continua su un insieme compatto (cioè chiuso e limitato), allora assume sia un massimo assoluto sia un minimo assoluto su quell'insieme.

In altre parole, esistono punti del dominio in cui la funzione raggiunge i suoi valori più alto e più basso.

Nota. Il teorema di Weierstrass è una condizione sufficiente ma non necessaria per l'esistenza dei punti di minimo e massimo assoluti. Quindi, se la funzione non è continua o le condizioni del teorema non sono soddisfatte, potrebbero comunque esistere dei punti in cui la funzione raggiunge il minimo o il massimo assoluto.

Un esempio pratico

Considero la funzione di due variabili nell'intorno \( x^2 + y^2 \leq 1 \)

\[ f(x,y) = x^2 + y^2 \]

In pratica, devo trovare i punti di minimo e massimo della funzione dentro un cerchio di raggio 1 centrato nell'origine degli assi.

Le derivate parziali della funzione sono

$$ \frac{ \partial f }{ \partial x}   = 2x $$

$$ \frac{ \partial f }{ \partial y} = 2y $$

Scrivo un sistema di equazioni per trovare i punti stazionari, ossia quelli in cui la derivata parziale si annulla.

$$ \begin{cases}  2x=0 \\ \\ 2y=0 \end{cases} $$

$$ \begin{cases}  x=0 \\ \\ y=0 \end{cases} $$

In questo caso c'è un solo punto stazionario nell' nell'origine \((0,0)\). 

Questo è un minimo locale facile da individuare, perché la funzione vale \( 0^2+0^2 = 0 \) e il suo codominio è l'insieme dei numeri reali non negativi. Quindi, non può restituire valori inferiori a zero.

Ora devo anche verificare se ci sono punti singolari e punti di confine da studiare.

In questa funzione non ci sono punti singolari all'interno del dominio (il cerchio di raggio 1) ma c'è però un bordo.

Poiché sui bordi vale \(x^2 + y^2 = 1\) che è il massimo ottenibile nell'intorno, tutti i punti di confine sono dei punti di massimo della funzione.

Pertanto, la funzione ha un minimo nell'origine e infiniti punti di massimo sui bordi.

Esempio 2

In questo esercizio devo trovare i massimi e minimi locali della funzione:

\[ f(x,y) = xy \]

nel dominio:

\[ D = \{ (x,y) \, | \, x^2 + y^2 \leq 1 \} \]

cioè sempre dentro il cerchio di raggio 1 centrato nell'origine, come prima, ma la funzione è più complessa perché mischia x e y.

1] Punti stazionari

Per prima cosa cerco i punti stazionari dentro il dominio.

Calcolo le derivate parziali:

\[ \frac{\partial f}{\partial x} = y \]

\[ \frac{\partial f}{\partial y} = x \]

Costruisco un sistema con le derivate parziali uguali a zero.

$$ \begin{cases}  x=0 \\ \\ y=0 \end{cases} $$

Anche in questo caso il punto critico è \((0,0)\) ossia l'origine

Valutiamo la funzione nell'origine

\[ f(0,0) = 0 \]

In questo caso però non posso affermare che sia un minimo, perché il codominio della funzione è l'intero insieme dei numeri reali. Quindi, per il momento non posso dire nulla.

2] Punti singolari

La funzione non ha punti singolari nel dominio che sto studiando.

3] Il bordo

Sul bordo la funzione vale

\[ x^2 + y^2 = 1 \]

Posso parametrizzare il bordo usando le coordinate polari:

\[ x = \cos\theta, \quad y = \sin\theta \]

Dove \(\theta\) è l'angolo che va da \(0\) a \(2\pi\) radianti.

Quindi, la funzione \(f\) diventa:

\[ f(\cos\theta, \sin\theta) = \cos\theta \sin\theta \]

Sapendo che \(\sin(2\theta) = 2\sin\theta\cos\theta\), posso riscriverla in questa forma:

\[ f(\theta) = \frac{1}{2} \sin(2\theta) \]

Ora cerco il massimo e il minimo di \(f(\theta)\).

La funzione \(\sin(2\theta)\) varia tra \(-1\) e \(1\), quindi la funzione \(\frac{1}{2} \sin(2\theta)\) ha un valore compreso tra \(-\frac{1}{2}\) e \(\frac{1}{2}\).

Questi due valori sono il massimo e il minimo possibile della funzione

• Massimo: \( f(\theta) = \frac{1}{2}\)
• Minimo: \( f(\theta) = -\frac{1}{2}\)

Dove si trovano? Per saperlo controllo quando la funzione $ \sin(2\theta)  $ restituisce 1 o -1.

• $ \sin(2\theta) = 1 $ si verifica quando $ 2\theta = \frac{\pi}{2} $ cioè quando $ \theta = \frac{\pi}{4} $. Quindi, il punto di massimo si trova alle coordinate \(x = \cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}\), \(y = \sin\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}\)
• $ \sin(2\theta) = -1 $ si verifica quando $ 2\theta = \frac{3\pi}{2} $ cioè quando $ \theta = \frac{3\pi}{4} $. Quindi, il punto di minimo si trova alle coordinate \(x = \cos\left(\frac{3\pi}{4}\right) = -\frac{\sqrt{2}}{2}\), \(y = \sin\left(\frac{3\pi}{4}\right) = \frac{\sqrt{2}}{2}\)

In conclusione, il massimo globale si trova nel punto \(\left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\) dove la funzione restituisce il valore maggiore possibile \(\frac{1}{2}\).

Il minimo globale si trova nel punto \(\left( -\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\) dove la funzione restituisce il valore minore possibile \(-\frac{1}{2}\).

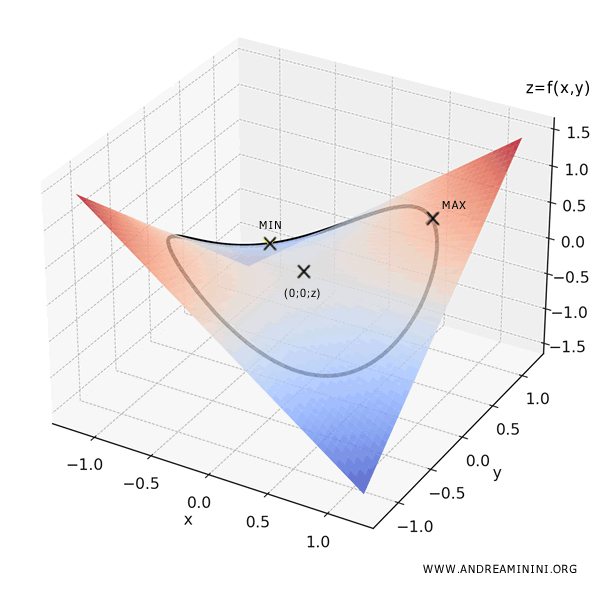
Pertanto, in questa funzione il minimo e il massimo globale si trovano entrambi sul bordo del dominio che nel grafico è rappresentato con una linea nera.

E il punto \((0,0)\)? È un punto di sella, non è né un massimo né un minimo globale.

Esempio 3

Considero la funzione nel dominio \( A = [0,1] \times [0,2] \)

\[ f(x,y) = 2x + 3y \]

L'insieme \( A \) è chiuso e limitato, quindi compatto, e la funzione \( f \) è continua perché è un polinomio in due variabili.

Per il teorema di Weierstrass la funzione \( f \) ammette minimo e massimo assoluti su \( A \).

In questo caso per trovare il minimo e il massimo basta seguire un ragionamento intuitivo.

La funzione \( f(x,y) \) è una funzione lineare: cresce al crescere di \( x \) e di \( y \).

Quindi, il minimo assoluto si ottiene assegnando a \( x \) e \( y \) i valori più piccoli nel dominio, cioè \( x=0 \) e \( y=0 \).

\[ f(0,0) = 2 \cdot 0 + 3 \cdot 0 = 0 \]

Il massimo assoluto, invece, si ottiene assegnando a \( x \) e \( y \) i valori più grandi permessi dal dominio, cioè \( x=1 \) e \( y=2 \).

\[ f(1,2) = 2 \cdot 1 + 3 \cdot 2 = 2 + 6 = 8 \]

Questo esempio mostra che, se la funzione è semplice (come un polinomio di primo grado), è possibile individuare il massimo e il minimo senza bisogno di calcolare derivate, ma semplicemente analizzando l'andamento della funzione.

Il metodo delle linee di livello

Il metodo delle linee di livello è una tecnica grafica per trovare il massimo o minimo di una funzione \( f(x, y) \) su un insieme \( A \) (dominio della funzione).

E' un metodo intuitivo e visivo, particolarmente utile per funzioni semplici e domini poligonali.

Come funziona

Ecco i passi da seguire

1. Disegno l'insieme \( A \) sul piano \( (x,y) \)
2. Disegno le linee di livello di \( f(x, y) \), cioè le curve dove la funzione è costante:  \[ f(x, y) = \lambda \]
3. Il massimo si trova cercando la linea di livello più alta (cioè col maggiore \( \lambda \)) che interseca o tocca \( A \). Analogamente, il minimo è la linea col minore \( \lambda \) che tocca \( A \).

Esempio

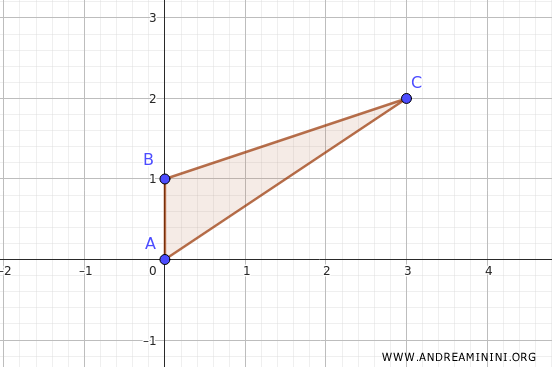
Considero la \( f(x, y) = 2x - y \) e il dominio \( A \) è il triangolo con vertici in \( (0,0),(0,1), (3,2)\)

Disegno l'insieme del dominio \( A \) sul piano. In questo caso è un triangolo.

Per trovare il massimo e il minimo di \( f(x, y) \) su \( A \) costruisco le linee di livello della funzione:

\[ f(x, y) = \lambda \]

\[ 2x - y = \lambda \]

\[ y = 2x - \lambda \]

In questo caso le linee di livello sono rette parallele, inclinate verso il basso (pendenza 2). Al crescere di \( \lambda \), la retta trasla verso destra.

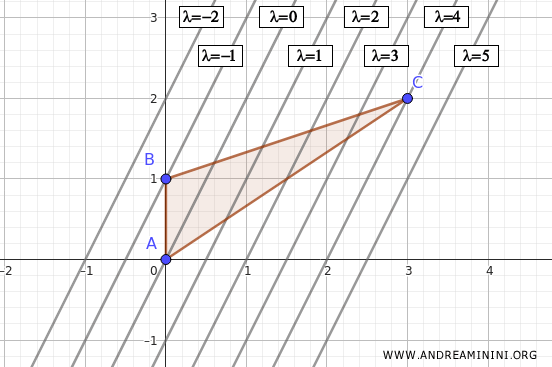
La linea di livello con \( \lambda \) più alto tocca l'intorno \( A \) nel punto \( (3,2) \).

In questo punto la funzione raggiunge il suo massimo in \( A \):

\[ f(3, 2) = 2x-y = 2 \cdot 3 - 2 = 6 - 2 = 4 \]

Per trovare il minimo seguo la stessa procedura, cerco la linea di livello con \( \lambda \) più basso che interseca ancora il dominio.

La linea di livello con \( \lambda \) più basso tocca l'intorno \( A \) nel punto \( (0,1) \).

In questo punto la funzione raggiunge il suo minimo in \( A \):

\[ f(0, 1) = 2x-y = 2 \cdot 0 - 1 = -1 \]

In questo modo ho trovato il minimo e il massimo della funzione semplicemente osservando le linee di livello e il dominio della funzione.

Il metodo della parametrizzazione

Il metodo della parametrizzazione è una tecnica usata per studiare una funzione e trovare massimi e minimi assoluti su un dominio delimitato, in particolare lungo il bordo del dominio.

E' utile quando voglio studiare una funzione \( f(x, y) \) su un dominio chiuso e limitato.

Come funziona

Il bordo del dominio viene descritto tramite parametrizzazioni, cioè trasformazioni che riscrivono ogni pezzo del bordo usando un parametro \( t \).

1. Divido il bordo in tratti semplici (ad es. linee o curve).
2. Parametrizzo ogni tratto con una funzione \( \gamma(t) = (x(t), y(t)) \) che descrive quel tratto.
3. Sostituisco nella funzione e ottengo \( f(x(t), y(t)) \), una funzione di \( t \).
4. Trovo il massimo e il minimo sul bordo.
5. Ripeto per ogni tratto del bordo.
6. Confronto tutti i valori ottenuti per individuare il massimo e il minimo globale nel dominio.

Questo metodo mi permette di trasformare uno studio in due variabili in uno in una variabile.

È molto utile per domini delimitati da curve o segmenti, come rettangoli, cerchi, ecc.

Ad esempio, se un lato del bordo è il segmento da \((x,y)= (2,1) \) a \( (x,y)=(5,1) \), allora una parametrizzazione è:  \[  x(t) = t,\quad y(t) = 1,\quad \text{con } t \in [2,5] \] La funzione \( f(x,y) \) diventa così una funzione di una variabile: \[ f(x(t), y(t)) = f(t, 1) \]

Esempio pratico

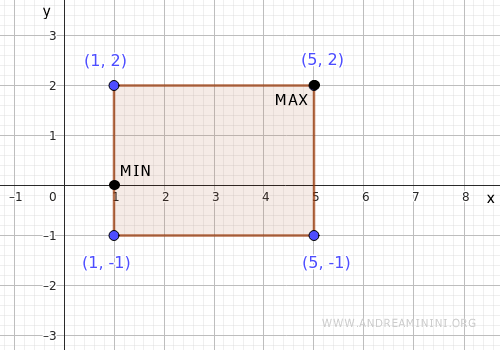
Considero la funzione di due variabili

$$ f(x,y) = x^2 + y^2 $$

nel dominio rettangolare

$$ A = [1,5] \times [-1,2] $$

Devo trovare i punti di minimo e massimo della funzione nel dominio A.

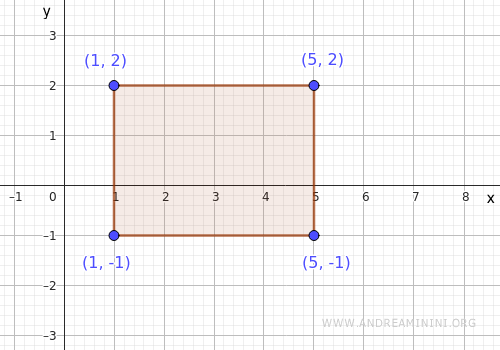
Quindi, studio i punti stazionari interni, i punti singolari interni e il bordo.

1]  Studio dei punti stazionari interni

Calcolo il gradiente della funzione:

\[ \nabla f(x,y) = (2x, 2y) \]

Poi cerco dove si annulla:

$$ \begin{cases} 2x=0 \\ \\ 2y = 0 \end{cases} $$

Il gradiente si annulla solo nel punto \( (0,0) \)

\[ \nabla f(x,y) = (0,0) \Rightarrow x = 0,\ y = 0 \]

Ma il punto \( (0,0) \) non appartiene al dominio \( [1,5] \times [-1,2] \) della funzione. Quindi, non ci sono punti critici interni.

2] Studio dei punti singolari interni

Cerco in quali punti la funzione non è differenziabile, ossia non ha derivate parziali.

In questo caso non ci sono punti singolari interni.

3] Studio i punti del bordo

Per studiare i punti del bordo utilizzo il metodo della parametrizzazione.

Il bordo è un rettangolo formato da 4 lati. Li studio uno per uno.

• Lato in alto
  Il lato in alto è un segmento orizzontale che va dal punto \( (1,2) \) al punto \( (5,2) \). Quindi lo parametrizzo tramite la funzione \( \gamma(t) = (t, 2) \), con \( t \in [1,5] \).
  
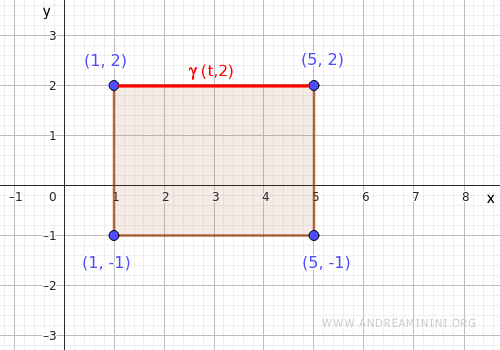
  Sostituisco \( (t,2) \) nella funzione $ x^2+y^2 $ e ottengo $$ f(t,2) = t^2 + 4 $$ Ora cerco il minimo e il massimo di $ f(t,2) $ nell'intervallo chiuso \(t \in [1,5] \)
  • min in \( t=1 \): \( f(1,2) = 1 + 4 = 5 \)
  • max in \( t=5 \): \( f(5,2) = 25 + 4 = 29 \)
• Lato in basso
  Il lato in basso è un segmento orizzontale che va dal punto dal punto \( (1,-1) \) al punto \( (5,-1) \) e lo parametrizzo con la funzione  \( \gamma(t) = (t, -1) \), con \( t \in [1,5] \).
  
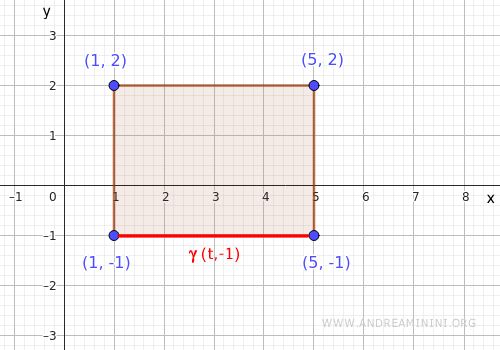
  Sostituisco \( (t,-1) \) nella funzione $ x^2+y^2 $ e ottengo $$ f(t,-1) = t^2 + 1 $$ Poi cerco il minimo e il massimo di $ f(t,-1) $ nell'intervallo chiuso \(t \in [1,5] \)
  • min: \( f(1,-1) = 1 + 1 = 2 \) 
  • max: \( f(5,-1) = 25 + 1 = 26 \)
• Lato a destra
  Il lato a destra è un segmento verticale che va dal punto \( (5,-1) \) al punto \( (5,2) \). Lo parametrizzo tramite la funzione \( \gamma(t) = (5, t) \), con \( t \in [-1,2] \).
  
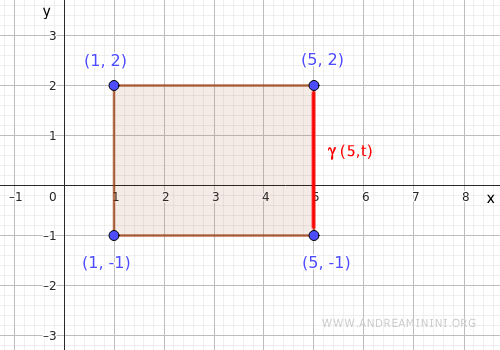
  Sostituisco \( (5,t) \) nella funzione $ x^2+y^2 $ e ottengo $$ f(5,t) = 25 + t^2  $$ Ora cerco il minimo e il massimo di $ f(5,t) $ nell'intervallo chiuso \( t \in [-1,2] \)
  • min in \( t=0 \): \( f(5,0) = 25 + 0 = 25 \) 
  • max in \( t= 2 \): \( f(5,2) = 25 + 4 = 29 \)
• Lato a sinistra
  Il lato a sinistra è un segmento verticale che va dal punto \( (1,-1) \) al punto \( (1,2) \) e lo parametrizzo tramite la funzione \( \gamma(t) = (1, t) \), con \( t \in [-1,2] \).
  
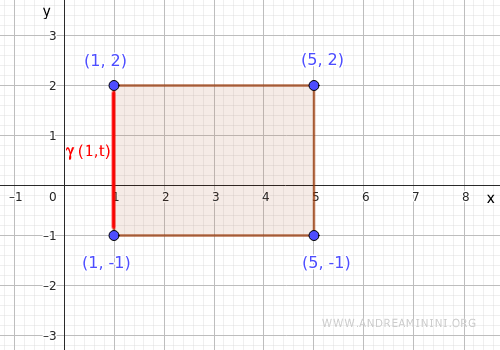
  Sostituisco \( (1,t) \) nella funzione $ x^2+y^2 $ e ottengo $$ f(1,t) = 1+t^2 $$ Poi cerco il minimo e il massimo di $ f(1,t) $ nell'intervallo chiuso \( t \in [-1,2] \)
  • min: \( f(1,0) = 1 + 0 = 1 \)
  • max: \( f(1,2) = 1 + 4 = 5 \)

Ricapitolando, ho trovato i seguenti punti del bordo in cui potrebbero essere il minimo e il massimo della funzione.

\[
\begin{array}{|c|c|}
\hline
\textbf{Punto} & \textbf{f(x,y)} & \textbf{Natura del punto} \\
\hline
(1,2) &  5  &\\
(5,2) &  29 & massimo \\
(5,0) & 25 & \\
(5,-1) & 26 & \\
(1,-1) &  2 & \\
(1,0) & 1 & minimo \\
\hline
\end{array}
\]

In questo caso, il minimo assoluto della funzione $ x^2+y^2 $ si trova nel punto  \( (1,0) \) mentre il massimo assoluto nel punto \( (5,2) \). Gli altri punti posso scartarli.

Il metodo dei moltiplicatori di Lagrange

Il metodo dei moltiplicatori di Lagrange è una tecnica per trovare i massimi e minimi locali di una funzione vincolata.

È particolarmente utile per ottimizzare una funzione $f(x, y)$ soggetta a un vincolo del tipo $g(x, y) = 0$.

L'obiettivo è trovare i punti $(x, y)$ che massimizzano o minimizzano $f(x, y)$, sotto il vincolo $g(x, y) = 0$.

L'idea base è che se $f(x, y)$ ha un estremo sotto il vincolo $g(x, y) = 0$, allora i gradienti di $f$ e $g$ devono essere paralleli  in quel punto:

$$ \nabla f(x, y) = \lambda \nabla g(x, y) $$

Dove:

• $\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right)$ è il gradiente di $f$
• $\nabla g = \left( \frac{\partial g}{\partial x}, \frac{\partial g}{\partial y} \right)$ è il gradiente del vincolo $ g $
• $\lambda$ è il moltiplicatore di Lagrange

Come funziona

Ecco la procedura passo per passo

1. Scrivo le equazioni: $$
   \begin{cases}
   \frac{\partial f}{\partial x} = \lambda \frac{\partial g}{\partial x} \\
   \frac{\partial f}{\partial y} = \lambda \frac{\partial g}{\partial y} \\
   g(x, y) = 0
   \end{cases}
   $$
2. Risolvo il sistema di tre equazioni in tre incognite: $x, y, \lambda$
3. Trovo i punti critici $(x, y)$
4. Valuto la funzione $f(x, y)$ nei punti che ho appena trovato per determinare quale dà il massimo e quale il minimo

Nota. Questo metodo non restituisce direttamente i punti di massimo e minimo, ma solo i punti critici in cui potrebbero trovarsi. Quindi, devo valutare singolarmente ogni punto critico per capire di cosa si tratta veramente.

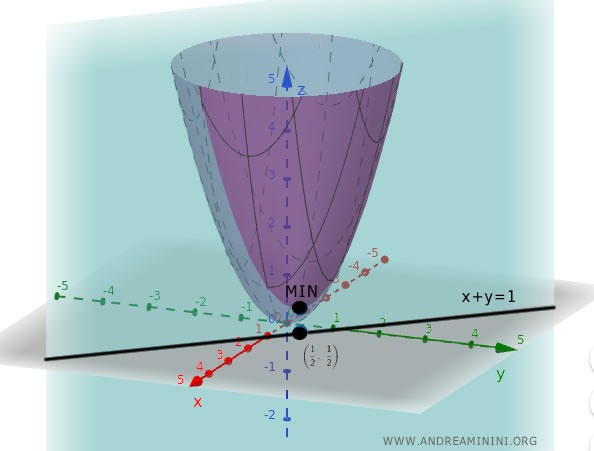
Esempio pratico

Considero la funzione di due variabili

$$ f(x, y) = x^2 + y^2 $$

Sotto il vincolo seguente:

$$ x + y = 1 $$

Per prima cosa devo esprimere il vincolo nella forma $ g(x,y)=0 $

$$ g(x,y)=  x + y - 1 = 0$$

Poi calcolo i gradienti

2. Calcola i gradienti delle funzioni $ f $ e $ g $:

$$ \nabla f = (2x, 2y) $$

$$ \nabla g = (1, 1) $$

A questo punto scrivo il sistema di Lagrange:

$$ \begin{cases}
2x = \lambda \cdot 1 \\
2y = \lambda \cdot 1 \\
x + y = 1
\end{cases}
\Rightarrow
\begin{cases}
\lambda = 2x \\
\lambda = 2y \\
x + y = 1
\end{cases}
$$

Sostituisco $ \lambda=2x $ nella seconda equazione $2x = 2y$ e ricavo che $x = y$

$$ \begin{cases}
\lambda = 2x \\
2x = 2y \\
x + y = 1
\end{cases}
\Rightarrow
\begin{cases}
\lambda = 2x \\
x = y \\
x + y = 1
\end{cases}
$$

Quindi, sapendo che $ x =y $, sostituisco $ y $ nella terza equazione e ricavo che $ x = \frac{1}{2} $

$$ \begin{cases}
\lambda = 2x \\
x = y \\
x + x = 1
\end{cases}
\Rightarrow
\begin{cases}
\lambda = 2x \\
x = y \\
2x  = 1
\end{cases} \Rightarrow
\begin{cases}
\lambda = 2x \\
x = y \\
x  = \frac{1}{2}
\end{cases}
$$

Poiché $ x=y $ anche $ y = \frac{1}{2}$

$$ \begin{cases}
\lambda = 2x \\
y = \frac{1}{2} \\
x  = \frac{1}{2}
\end{cases}
$$

Quindi, il punto critico da valutare è $ \left( \frac{1}{2}, \frac{1}{2} \right) $

Infine, valuto il punto critico

$$ f \left( \frac{1}{2}, \frac{1}{2} \right) = \left( \frac{1}{2} \right)^2 + \left( \frac{1}{2} \right)^2 = \frac{1}{2} $$

Deduco che si tratta di un minimo sotto il vincolo $ x+y=1 $, dato che la funzione $f$ è sempre crescente con la distanza dall’origine e il vincolo è una retta.

Il metodo dei punti stazionari del vincolo

Il sistema dei punti stazionari del vincolo si riferisce all'insieme di equazioni che identificano i punti in cui il gradiente del vincolo si annulla, ovvero: $$ \begin{cases} \Phi(x, y) = 0 \\ \frac{\partial \Phi}{\partial x}(x, y) = 0 \\ \frac{\partial \Phi}{\partial  }(x, y) = 0\end{cases} $$ Dove $\Phi(x, y)$ rappresenta la funzione vincolo.

Questi punti sono chiamati punti critici o punti stazionari del vincolo perché in essi il gradiente del vincolo è nullo.

In termini geometrici, questo significa che la curva definita dal vincolo presenta un comportamento particolare in questi punti, come un punto angoloso o una cuspide.

Questo metodo è molto utile nei casi in cui il gradiente del vincolo è nullo, cioè quando non posso applicare il metodo dei moltiplicatori di Lagrange.

Nota. Il metodo dei moltiplicatori di Lagrange non è applicabile quando il gradiente del vincolo è nullo, poiché richiede che il gradiente del vincolo sia diverso da zero per garantire la regolarità del problema.

Tuttavia, non garantisce soluzioni, perché spesso il sistema risulta incompatibile o senza punti reali.

Inoltre, anche quando ha soluzioni, queste vanno verificate una per una per stabilire se rappresentano massimi o minimi vincolati.

I punti stazionari del vincolo rappresentano solo dei possibili candidati per massimi o minimi vincolati e devono essere analizzati separatamente.

Esempio

Considero la funzione di due variabili

$$ f(x,y) = x+y $$

Entro il vincolo:

$$ \Phi(x, y) = (x - 1)^2 + y^2(y - 2)^2 $$

Calcolo le derivate parziali del vincolo rispetto alle variabili $ x $ e $ y $

$$ \frac{\partial \Phi}{\partial x} = 2(x - 1) $$

$$ \frac{\partial \Phi}{\partial y} = 2y(y - 2)^2 + y^2 \cdot 2(y - 2) $$

Quindi, costruisco il sistema di equazioni

$$
\begin{cases}
\Phi(x, y) = 0 \\
\frac{\partial \Phi}{\partial x}(x, y) = 0 \\
\frac{\partial \Phi}{\partial y}(x, y) = 0
\end{cases}
$$

$$ \begin{cases}
\Phi(x, y) = (x - 1)^2 + y^2(y - 2)^2 = 0 \\
\Phi_x = 2(x - 1) = 0 \\
\Phi_y = 2y(y - 2)^2 + y^2 \cdot 2(y - 2) = 0
\end{cases}
$$

Nella seconda equazione ottengo $ x=1 $

$$ \begin{cases}
(x - 1)^2 + y^2(y - 2)^2 = 0 \\
x =1 \\
2y(y - 2)^2 + y^2 \cdot 2(y - 2) = 0
\end{cases}
$$

Sostituisco $ x=1 $ nella prima equazione e ottengo $ y= 0 $ oppure $ y=2 $

$$ \begin{cases}
(1 - 1)^2 + y^2(y - 2)^2 = 0 \\
x =1 \\
2y(y - 2)^2 + y^2 \cdot 2(y - 2) = 0
\end{cases} \Rightarrow  \begin{cases}
y^2(y - 2)^2 = 0 \\
x =1 \\
2y(y - 2)^2 + y^2 \cdot 2(y - 2) = 0
\end{cases}
$$

Quindi due punti stazionari del vincolo da controllare sono:

$$ (1, 0) $$

$$ (1, 2) $$

Valuto la funzione $ f $ in questi punti:

$$ f(1, 0) = 1 $$

$$ f(1, 2) = 3 $$

Pertanto $ (1,0) $ è il minimo $ f(1,0)=1$ mentre $ (1,2) $ è il massimo $ f(1,2)=3 $ della funzione.

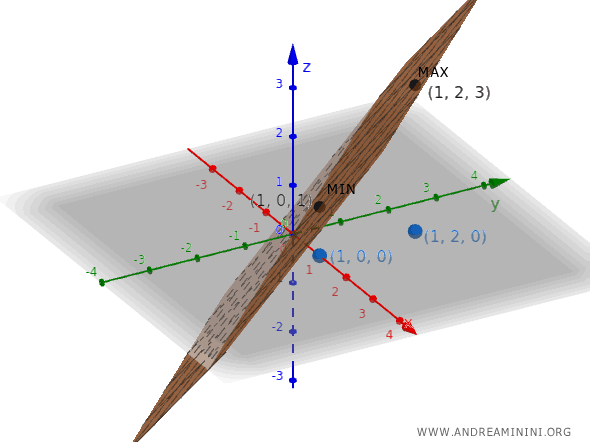
Da notare che in questo caso il vincolo $ \Phi(x, y) = 0  $ si riduce essenzialmente ai soli due punti $ (1,0) $ e $ (1,2) $, quindi tutta l'analisi poteva essere evitata una volta capito questo.

Nota. In questo caso il metodo di Lagrange non è applicabile perché in entrambi i punti il gradiente si annulla $\nabla \Phi = 0$. Ad esempio, in questo esercizio il gradiente del vincolo $ \nabla \Phi(x, y) = \left( \frac{\partial \Phi}{\partial x}, \frac{\partial \Phi}{\partial y} \right) $ è composto dalle derivate parziali seguenti: $$ \frac{\partial \Phi}{\partial x} = \frac{\partial}{\partial x} \left[(x - 1)^2 + y^2(y - 2)^2\right] = 2(x - 1) $$ $$ \frac{\partial \Phi}{\partial y} = \frac{\partial}{\partial y} \left[y^2 (y - 2)^2\right] $$ Nel caso del punto $ (1,0) $ ottengo: $$ \frac{\partial \Phi}{\partial x} = 2(1 - 1) = 0 $$ $$\frac{\partial \Phi}{\partial y} = 2 \cdot 0 \cdot 4 + 2 \cdot 0^2 \cdot (-2) = 0 + 0 = 0 $$ Nel caso del punto $ (1,2) $ ottengo $$\frac{\partial \Phi}{\partial x} = 2(1 - 1) = 0 $$ $$\frac{\partial \Phi}{\partial y} = 2 \cdot 2 \cdot 0 + 2 \cdot 4 \cdot 0 = 0 + 0 = 0 $$ Quindi, in entrambi i casi il gradiente si annulla $$ \nabla \Phi(1, 0) = (0, 0) $$ $$ \nabla \Phi(1, 2) = (0, 0) $$ Perciò, nel metodo dei moltiplicatori non esiste nessun $ \lambda $ che soddisfi l'equazione: $$ \nabla f = \lambda \nabla \Phi \Rightarrow \nabla f = \lambda \cdot (0, 0) = (0, 0) $$ Quindi, il metodo di Lagrange non si può applicare.

La matrice Hessiana

Per trovare il minimo e il massimo in una funzione di due variabili, tipo \( f(x, y) \), posso anche usare la matrice Hessiana.

La matrice hessiana è una matrice quadrata composta dalle derivate parziali seconde della funzione.\[
H = \begin{pmatrix}
\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
\frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2}
\end{pmatrix}
\]

Sulla diagonale principale della matrice scrivo le derivate parziali seconde pure, $ \frac{ \partial^2 f}{\partial x^2} $ e $ \frac{\partial^2 f}{\partial y^2 } $, quelle in cui derivo due volte la stessa variabile.

Sulla diagonale secondaria, invece, scrivo le derivate parziali seconde miste $ \frac{\partial^2 f}{\partial x \partial y} $ e $ \frac{\partial^2 f}{\partial y \partial x } $, quelle in cui derivo prima per una variabile e poi per l'altra.

Una volta costruita la matrice hessiana, sostituisco alle variabili $ x $ e $ y $ i valori del punto critico che voglio verificare.

Nota. Se la matrice è composta da soli numeri, posso usarla così come è per verificare qualsiasi punto critico della funzione.

Poi calcolo il determinante \( \Delta \) della matrice.

• Se \( \Delta > 0 \) e \( \frac{\partial^2 f}{\partial x^2} > 0 \), ho un minimo locale nel punto.
• Se \( \Delta > 0 \) e \( \frac{\partial^2 f}{\partial x^2} < 0 \), ho un massimo locale.
• Se \( \Delta < 0 \), è un punto di sella cioè né minimo né massimo.
• Se \( \Delta = 0 \), la Hessiana non mi dice nulla e devo usare altri metodi per studiare la funzione.

Esempio

Nell'esercizio precedente sulla funzione

\[ f(x,y) = xy \]

nel dominio:

\[ D = \{ (x,y) \, | \, x^2 + y^2 \leq 1 \} \]

avevo trovato un punto critico alle coordinate P(0,0).

Per verificare se è un minimo o un massimo costruisco la matrice Hessiana della funzione.

\[
H = \begin{pmatrix}
\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
\frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2}
\end{pmatrix}
\]

Le derivate parziali prime sono:

• $ \frac{\partial f}{\partial x} = y $
• $ \frac{\partial f}{\partial y} = x $

Le derivate seconde che servono per la Hessiana sono:

• \(\frac{\partial^2 f}{\partial x^2} = 0\) (perché la derivata di \(y\) rispetto a \(x\) è zero, non c'è \(x\) in \(y\))
• \(\frac{\partial^2 f}{\partial y^2} = 0\) (idem: derivata di \(x\) rispetto a \(y\) è zero)
• \(\frac{\partial^2 f}{\partial x \partial y} = 1\) (derivata di \(y\) rispetto a \(y\) è 1)
• \(\frac{\partial^2 f}{\partial y \partial x} = 1\) (derivata di \(x\) rispetto a \(x\) è 1)

Quindi la matrice Hessiana è

\[ H = \begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}
\]

Nella matrice Hessiana non ci sono le variabili $ x $ e $ y $, quindi posso usarla direttamente per verificare il punto critico P(0;0) senza sostituire i valori delle variabili $ x=0 $ e $ y= 0 $.

A questo punto calcolo il determinante della matrice Hessiana:

\[ \Delta = (0)(0) - (1)(1) = -1 \]

Il determinante è negativo \(\Delta < 0\), questo significa che il punto critico P(0;0) è un punto di sella, cioè né massimo né minimo.

E' lo stesso risultato a cui ero giunto nell'esercizio precedente.

Esempio 2

Considero la funzione:

\[ f(x,y) = x^4 - 2xy + y^4 \]

nel dominio:

\[ D = \{ (x,y) \mid x^2 + y^2 \leq 4 \} \]

Il che equivale a un cerchio di raggio 2 centrato nell'origine (0,0).

Calcolo le derivate parziali prime:

• \(\frac{\partial f}{\partial x} = 4x^3 - 2y\)
• \(\frac{\partial f}{\partial y} = 4y^3 - 2x\)

Le metto a sistema eguagliandole a zero.

\[ \begin{cases} 4x^3 - 2y = 0 \\ \\ 4y^3 - 2x = 0 \end{cases} \] 

Risolvo il sistema

\[ \begin{cases} y = 2x^3  \\ \\ 4(2x^3)^3 - 2x = 0 \end{cases} \]

\[ \begin{cases} y = 2x^3  \\ \\ 32x^9 - 2x = 0 \end{cases} \]

\[ \begin{cases} y = 2x^3  \\ \\ 2x(16x^8 - 1) = 0 \end{cases} \]

Quindi, le soluzioni sono\(2x = 0\) ossia \(x = 0\) e \(16x^8 = 1\) ossia \(x^8 = \frac{1}{16}\)

\[ x = \pm  \frac{1}{ \sqrt[8]{16}}  =  \pm  \frac{1}{ \sqrt[8]{2^4}} =  \pm  \frac{1}{ \sqrt[2]{2}} \approx 0.707 \]

Quindi:

\[ x = \pm \frac{1}{\sqrt{2}} \]

Ora, sostituisco i valori della $ x $ nella prima equazione \(y = 2x^3\) del sistema:

• Se \(x = 0\), \(y = 0\)
• Se \(x = \frac{1}{\sqrt{2}}\): \[ y = 2\left(\frac{1}{\sqrt{2}}\right)^3 = 2\left(\frac{1}{2\sqrt{2}}\right) = \frac{1}{\sqrt{2}}
  \]
• Se \(x = -\frac{1}{\sqrt{2}}\): \[ y = 2\left(-\frac{1}{\sqrt{2}}\right)^3 = 2\left(-\frac{1}{2\sqrt{2}}\right) = -\frac{1}{\sqrt{2}}
  \]

Quindi i punti critici sono:

• \((0,0)\)
• \(\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\)
• \(\left(-\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}\right)\)

Tutti questi punti stanno dentro il cerchio di raggio 2, ovviamente (perché \((x^2+y^2) \leq 4\)).

Costruisco la matrice Hessiana

Le derivate seconde sono:

• \(\frac{\partial^2 f}{\partial x^2} = 12x^2\)
• \(\frac{\partial^2 f}{\partial y^2} = 12y^2\)
• \(\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x} = -2\)

Quindi la Hessiana è:

\[
H = \begin{pmatrix}
12x^2 & -2 \\
-2 & 12y^2
\end{pmatrix}
\]

A questo punto valuto la Hessiana nei punti critici

1] Punto \((0,0)\):

Sostituisco $ x=0 $ e $ y=0 $ nella Hessiana.

\[
H(0,0) = \begin{pmatrix}
0 & -2 \\
-2 & 0
\end{pmatrix}
\]

Poi calcolo il determinante:

\[ \Delta = (0)(0) - (-2)(-2) = -4 \]

Il determinante è negativo \(\Delta < 0\), quindi il punto (0,0) è un punto di sella.

2] Punto \(\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\):

Sostituisco $ x= \frac{1}{ \sqrt{2} } $ e $ y= \frac{1}{\sqrt{2}} $ nella Hessiana.

\[
H\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right) = \begin{pmatrix}
12\left(\frac{1}{2}\right) & -2 \\
-2 & 12\left(\frac{1}{2}\right)
\end{pmatrix} = \begin{pmatrix}
6 & -2 \\
-2 & 6
\end{pmatrix}
\]

Poi calcolo il determinante:

\[ \Delta = (6)(6) - (-2)(-2) = 36 - 4 = 32 \]

Il determinante è positivo \(\Delta > 0\) e \(\frac{\partial^2 f}{\partial x^2} = 6 > 0\), quindi il punto è un minimo locale.

3] Punto \(\left(-\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}\right)\):

Stesso discorso per simmetria rispetto al caso precedente.

\[
H\left( - \frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}\right) = \begin{pmatrix}
12\left( \frac{1}{2}\right) & -2 \\
-2 & 12\left(  \frac{1}{2}\right)
\end{pmatrix} = \begin{pmatrix}
6 & -2 \\
-2 & 6
\end{pmatrix}
\]

La matrice è sempre la stessa, quindi anche il determinante è identico.

\[ \Delta = (6)(6) - (-2)(-2) = 36 - 4 = 32 \]

Quindi anche questo punto è un minimo locale.

E così via.