Differenziabilità di una funzione di due variabili

Sia \( f: \mathbb{R}^2 \to \mathbb{R} \) una funzione reale di due variabili, si dice che \( f \) è differenziabile nel punto \( (x_0, y_0) \in \mathbb{R}^2 \) se esistono due numeri reali \( \alpha \) e \( \beta \) tali che: \[ f(x_0 + h,\ y_0 + k) = f(x_0, y_0) + \alpha h + \beta k + o\left(\sqrt{h^2 + k^2}\right) \]

Dove:

• \( h \) e \( k \) rappresentano piccoli spostamenti nelle direzioni \( x \) e \( y \)
• \( \sqrt{h^2 + k^2} \) è la distanza euclidea tra il punto \( (x_0, y_0) \) e il punto spostato \( (x_0 + h, y_0 + k) \)
• \( o\left(\sqrt{h^2 + k^2}\right) \) indica un termine infinitesimo di ordine superiore, ossia un errore che diventa trascurabile rispetto alla lunghezza dello spostamento

Se \( f \) è differenziabile in \( (x_0, y_0) \), allora esistono le derivate parziali in quel punto e valgono:

\[ \alpha = \frac{\partial f}{\partial x}(x_0, y_0) \]

\[ \beta = \frac{\partial f}{\partial y}(x_0, y_0) \]

Quindi, la formula della differenziabilità diventa:

\[ f(x_0 + h, y_0 + k) = f(x_0, y_0) + \frac{\partial f}{\partial x}(x_0, y_0) \cdot h + \frac{\partial f}{\partial y}(x_0, y_0) \cdot k +  o\left(\sqrt{h^2 + k^2}\right) \]

Sapendo che il gradiente di \( f \) nel punto \( (x_0, y_0) \) è composto dalle derivate parziali nel punto: \(
\nabla f(x_0, y_0) = \left( \frac{\partial f}{\partial x}(x_0, y_0), \frac{\partial f}{\partial y}(x_0, y_0) \right) \)

\[ f(x_0 + h, y_0 + k) = f(x_0, y_0) + \nabla f(x_0, y_0) \cdot (h, k) + o\left( \sqrt{h^2 + k^2} \right) \]

E ponendo il vettore degli incrementi come \( \vec{h} = (h, k) \) e il punto fisso \( \vec{x}_0 = (x_0, y_0) \), ottengo la stessa formula ma in notazione vettoriale.

\[ f(\vec{x}_0 + \vec{h}) = f(\vec{x}_0) + \nabla f(\vec{x}_0) \cdot \vec{h} + o(\|\vec{h}\|) \]

In parole più semplici, una funzione \( f(x, y) \) è differenziabile in un punto se, in un intorno di quel punto, si comporta quasi come un piano.

Vuol dire che la funzione può essere ben approssimata, localmente, da un piano tangente.

Questa è una proprietà molto più forte della sola esistenza delle derivate parziali e garantisce che la funzione sia regolare attorno a quel punto.

Nota. Il simbolo \( o\left(\sqrt{h^2 + k^2}\right) \) nasconde un limite: \[ \lim_{(h, k) \to (0, 0)} \frac{o\left(\sqrt{h^2 + k^2}\right)}{\sqrt{h^2 + k^2}} = 0 \] Significa che il termine di errore è olto più piccolo di \( \sqrt{h^2 + k^2} \) man mano che ci si avvicina al punto \((x_0, y_0)\). Questo assicura che il comportamento locale della funzione sia lineare. 

Come verificare se una funzione è differenziabile in un punto?

Nella pratica, per verificare se una funzione è differenziabile in un punto si utilizza il teorema del differenziale totale, piuttosto che la definizione di differenziabilità.

Esempio pratico

Considero la funzione:

\[ f(x, y) = x^2 + y^2 \]

Voglio analizzare la differenziabilità della funzione nel punto \( (x_0, y_0) = (1, 2) \).

Qundi, sostituisco le coordinate del punto \( (x_0, y_0) = (1, 2) \) nella formula di differenziabilità:

\[ f(x_0 + h,\ y_0 + k) = f(x_0, y_0) + \alpha h + \beta k + o\left(\sqrt{h^2 + k^2}\right) \]

\[ f(1 + h,\ 2 + k) = f(1, 2) + \alpha h + \beta k + o\left(\sqrt{h^2 + k^2}\right) \]

Sapendo che la funzione nel punto indicato restituisce $  f(1, 2) = 1^2 + 2^2 = 5 $

\[ f(1 + h,\ 2 + k) = 5 + \alpha h + \beta k + o\left(\sqrt{h^2 + k^2}\right) \]

I termini \(\alpha\) e \(\beta\) non sono numeri scelti a caso, ma rappresentano esattamente le derivate parziali della funzione nel punto \((x_0, y_0) = (1, 2) \):

\[ \alpha = \frac{\partial f}{\partial x}(1, 2)  = 2x = 2 \cdot 1 = 2 \]

\[ \beta = \frac{\partial f}{\partial y}(1, 2) = 2y = 2 \cdot 2 = 4 \]

Nota. I termini \(\alpha\) e \(\beta\) sono i coefficienti del piano tangente alla superficie nel punto \((x_0, y_0)\).  In pratica, danno la direzione e l'inclinazione con cui la funzione cresce o decresce, come succede per la tangente a una curva nel caso di una funzione di una sola variabile.

Quindi, i coefficienti del piano tangente nel punto \((x_0, y_0) = (1, 2) \) sono \( \alpha = 2 \) e \( \beta = 4 \).

\[ f(1 + h, 2 + k) = 5 + 2h + 4k + o\left(\sqrt{h^2 + k^2}\right) \]

A questo punto considero piccoli spostamenti $ h $ e $ k $ dal punto \((x_0, y_0) = (1, 2) \).

Ad esempio, se \( h = 0.01 \) e \( k = -0.02 \), allora il valore stimato sarà:

\[ f(1.01, 1.98) \approx 5 + 2 \cdot 0.01 + 4 \cdot (-0.02) = 5 + 0.02 - 0.08 = 4.94 \]

Il termine \( o(\cdot) \) è molto piccolo, quindi posso ometterlo.

Il valore reale della funzione si avvicina a 4.94 con un errore trascurabile ( 4.94 \approx 5 ).

Qual è l'equazione del piano tangente?

La formula del piano tangente è

\[ z = f(x_0, y_0) + \frac{\partial f}{\partial x}(x_0, y_0) \cdot (x - x_0) + \frac{\partial f}{\partial y}(x_0, y_0) \cdot (y - y_0) \]

Sapendo che \( (x_0,y_0 ) = (1,2) \) e \( f(1,2)= 5 \) 

\[ z = f(1, 2) + \frac{\partial f}{\partial x}(1, 2) \cdot (x - 1) + \frac{\partial f}{\partial y}(1, 2) \cdot (y - 2) \]

\[ z = 5 + \frac{\partial f}{\partial x}(1, 2) \cdot (x - 1) + \frac{\partial f}{\partial y}(1, 2) \cdot (y - 2) \]

Le derivate parziali sono\( \frac{\partial f}{\partial x}(1, 2) = 2x = 2 \cdot 1 = 2 \) e \( \frac{\partial f}{\partial y}(1, 2) =  2y = 2 \cdot 2 = 4 \)

\[ z = 5 + 2 \cdot (x - 1) + 4 \cdot (y - 2) \]

\[ z = 5 + 2x - 2 + 4y - 8 \]

\[ z = 2x + 4y - 5 \]

Questa è l'equazione del piano $ g(x,y)= 2x+4y+5 $ che approssima localmente la superficie della funzione $ f(x,y)=x^2+y^2 $ nel punto \( P(x_0, y_0,z) = (1, 2,5) \).

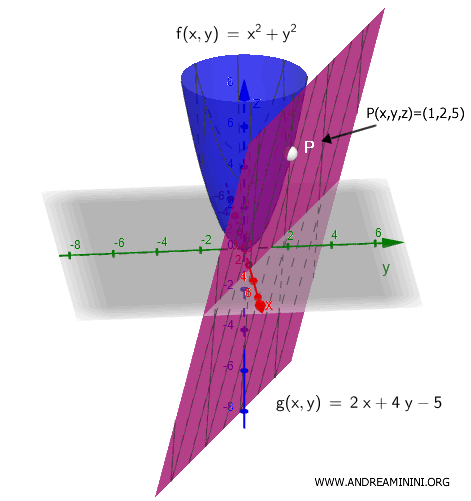
La differenziabilità delle funzioni con n variabili

La differenziabilità di una funzione nello spazio \( \mathbb{R}^n \) è meglio scriverla nella notazione vettoriale:

Una funzione \( f : \mathbb{R}^n \to \mathbb{R} \)  è differenziabile nel punto \( \vec{x}_0 \in \mathbb{R}^n \) se esiste un vettore \( \vec{\alpha} \in \mathbb{R}^n \) tale che: \[ f(\vec{x}_0 + \vec{h}) = f(\vec{x}_0) + \vec{\alpha} \cdot \vec{h} + o(\|\vec{h}\|) \quad \text{per } \vec{h} \to \vec{0} \]

Dove:

• \( \vec{x}_0 \) è un vettore che indica la posizione del punto fisso in cui voglio studiare la differenziabilità.
• \( \vec{h} \) è  il vettore di incremento, cioè uno spostamento da \( \vec{x}_0 \).
• \( \vec{\alpha} \) è il gradiente della funzione in \( \vec{x}_0 \).
• \( \vec{\alpha} \cdot \vec{h} \) è il prodotto scalare, cioè la parte lineare dello sviluppo.
• \( o(\|\vec{h}\|) \)è il termine di errore che tende a zero più velocemente di \( \|\vec{h}\| \).

Il limite \( \vec{h} \to \vec{0} \) indica che ci avviciniamo a \( \vec{x}_0 \) da tutte le direzioni possibili.

Se \( f \) è differenziabile in \( \vec{x}_0 \), allora esistono tutte le \( n \) derivate parziali in quel punto.

Come calcolare una derivata direzionale?

Se la funzione \( f \) è differenziabile in un punto \( \vec{x}_0 \), allora la derivata direzionale di \( f \) lungo una direzione \( \vec{v} \) è uguale al prodotto scalare tra il gradiente di \( f \) in quel punto e il vettore direzione \( \vec{v} \). 

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\nabla}f(x_0) \cdot \vec{v} \]

Dove \( \vec{v} \) è il vettore della direzione mentre \( \vec{\nabla}f(x_0) \) è il gradiente della funzione nel punto \( \vec{x}_0 \).

Il teorema del differenziale totale

Sia \( f(x, y) \) una funzione definita in un intorno di un punto \( (x_0, y_0) \in \mathbb{R}^2 \). Se le derivate parziali \( f_x \) e \( f_y \) esistono in un intorno di \( (x_0, y_0) \) e sono continue in quel punto, allora \( f \) è differenziabile in \( (x_0, y_0) \).

In tal caso, il differenziale totale di \( f \) in \( (x_0, y_0) \) è dato da:

\[ df = f_x(x_0, y_0) \, dx + f_y(x_0, y_0) \, dy \]

e la funzione può essere approssimata linearmente da:

\[ f(x, y) \approx f(x_0, y_0) + f_x(x_0, y_0)(x - x_0) + f_y(x_0, y_0)(y - y_0) \]

Il teorema del differenziale totale è particolarmente utile perché mi consente di dimostrare la differenziabilità di una funzione in un punto senza dover ricorrere alla definizione formale, che risulta spesso più complessa e tecnicamente laboriosa. 

Nota. Il teorema fornisce una condizione sufficiente, ma non necessaria, per la differenziabilità. Questo significa che se le derivate parziali esistono in un intorno del punto e sono continue nel punto, allora la funzione è differenziabile. Tuttavia, possono esistere funzioni differenziabili in un punto anche quando le derivate parziali non sono continue in quel punto.

Esempio

Considero di nuovo la funzione che ho già usato nell'esempio precedente:

\[ f(x, y) = x^2 + y^2 \]

Devo verificare che \( f \) è differenziabile nel punto \( (1, 2) \), applicando il teorema del differenziale totale.

Le derivate parziali della funzione esistono e sono:

\[ f_x(x, y) = \frac{\partial}{\partial x}(x^2 + y^2) = 2x \\ f_y(x, y) = \frac{\partial}{\partial y}(x^2 + y^2) = 2y \]

Le derivate parziali \( f_x(x, y) = 2x \) e \( f_y(x, y) = 2y \) sono entrambe delle funzioni polinomiali, quindi sono continue su tutto \( \mathbb{R}^2 \).

Quindi, le derivate parziali sono continue nell’intorno di \( (1, 2) \).

Pertanto, in base al teorema del differenziale totale, la funzione è differenziabile in quel punto perché ha le derivate parziali e queste sono continue nel punto.

Per completezza, posso scrivere anche il differenziale totale della funzione in \( (1, 2) \):

\[ df = f_x(1, 2) \, dx + f_y(1, 2) \, dy = 2 \cdot 1 \cdot dx + 2 \cdot 2 \cdot dy = 2dx + 4dy \]

In questo modo posso stabilire se una funzione è differenziabile in un punto rapidamente e senza utilizzare la definizione di differenziabilità.

Nota. In questo esempio semplice, la continuità delle derivate parziali è evidente, poiché si tratta di funzioni polinomiali. Tuttavia, in generale, per verificare la continuità di una derivata parziale è necessario controllare che il limite della derivata esista e coincida con il valore della derivata nel punto considerato. Ad esempio, se la derivata parziale è \( f_x(x, y) = 2x \), allora il limite è \[ \lim_{(x,y) \to (1,2)} 2x = 2 \cdot 1 = 2 \] che coincide con il valore della derivata parziale nel punto: \[ f_x(1,2) = 2x = 2 \cdot 1 = 2 \] Nel piano, e a maggior ragione nello spazio, un limite esiste solo se converge allo stesso valore lungo tutte le "infinite" traiettorie che portano al punto in questione, il che è di fatto impossibile da verificare direttamente. Per questo motivo, si ricorre al metodo delle coordinate polari traslate, che mi permette di analizzare il comportamento della funzione avvicinandosi al punto da tutte le direzioni, ma in modo più gestibile e rigoroso. Ad esempio, per capire cosa succede in prossimità di \( (1, 2) \), invece di studiare il limite con \( (x, y) \to (1, 2) \), effettuo un cambio di coordinate che trasla il sistema all’origine: \[ x = 1 + r \cos\theta,\quad y = 2 + r \sin\theta \] Effettuo il cambio di coordinate: \[ f_x(x, y) = 2x = 2(1 + r \cos\theta) = 2 + 2r \cos\theta \] Poi calcolo il limite per \( r \to 0 \): \[ \lim_{r \to 0} f_x(x, y) = \lim_{r \to 0} \left(2 + 2r \cos\theta\right) = 2 \] Questo limite è indipendente da \( \theta \), cioè dalla traiettoria seguita, e coincide con il valore della derivata $ f_x(x,y)=2x $ nel punto:\[f_x(1, 2) = 2 \cdot 1 = 2\] Dunque, il limite esiste, è indipendente dalla direzione con cui ci si avvicina al punto, e coincide con il valore della derivata parziale nel punto stesso. Pertanto, la funzione \( f_x(x, y) = 2x \) è continua nel punto \( (1, 2) \). Ovviamente, la stessa verifica va fatta anche per l'altra derivata parziale $ f_y(x,y) $.

Il teorema delle funzioni differenziabili

In altre parole, se una funzione è differenziabile in un punto, allora è continua lì, ha tutte le derivate parziali, e la derivata in qualunque direzione si calcola con un prodotto scalare.

Va detto che questo teorema non è invertibile e non vale l'inverso. 

Quindi, esistono funzioni con tutte le derivate parziali in \( \vec{x}_0 \) che non sono continue in \( \vec{x}_0 \), quindi non sono differenziabili.

Esempio

Considero la funzione di due variabili

\[ f(x, y) = \begin{cases} \displaystyle \frac{xy}{x^2 + y^2} & \text{se } (x, y) \neq (0, 0) \\ 0 & \text{se } (x, y) = (0, 0) \end{cases} \]

Calcolo le derivate parziali in un generico punto (x,y)

La derivata parziale rispetto a \( x \):

\[ \frac{\partial f}{\partial x}(x, y) =  \frac{(x^2 + y^2) \cdot y - xy \cdot 2x}{(x^2 + y^2)^2} = \frac{y(x^2 + y^2 - 2x^2)}{(x^2 +  y^2)^2} = \frac{y(-x^2 + y^2)}{(x^2 + y^2)^2} \]

La derivata parziale rispetto a \( y \):

\[ \frac{\partial f}{\partial y}(x, y) =  \frac{(x^2 + y^2) \cdot x - xy \cdot 2y}{(x^2 + y^2)^2} = \frac{x(x^2 + y^2 - 2y^2)}{(x^2 +  y^2)^2} = \frac{x(x^2 - y^2)}{(x^2 + y^2)^2} \]

Quindi, le derivate parziali della funzione in un generico punto (x,y) sono:

\[ \frac{\partial f}{\partial x}(x, y) =  \frac{y(-x^2 + y^2)}{(x^2 + y^2)^2} \]

\[ \frac{\partial f}{\partial y}(x, y) =   \frac{x(x^2 - y^2)}{(x^2 + y^2)^2} \]

Voglio studiare il comportamento di \( f \) in \( (0,0) \)

Le derivate parziali esistono in \( (0,0) \)

La derivata parziale rispetto a \( x \) è zero:

\[ \frac{\partial f}{\partial x}(x, 0) = \frac{0(0^2 - x^2)}{(x^2 + 0^2)^2} = 0 \]

Anche la derivata rispetto a \( y \) è zero:

\[ \frac{\partial f}{\partial y}(0, y) = \frac{0(0^2 - y^2)}{(0^2 + y^2)^2} = 0  \]

Pertanto, derivate parziali esistono e valgono entrambe 0.

Ora studio il limite della funzione in \( (0,0) \), lungo direzioni diverse.

Ad esempio, la derivata direzionale lungo la direzione \( y = x \) ossia \( \vec{v} = (1, 1) \) della funzione è

\[ D_{\vec{v}}f(0,0) = \lim_{h \to 0} \frac{f(h, h) - f(0,0)}{h} \]

Sapendo che \( \frac{xy}{x^2 + y^2} \) ottengo \( f(h,h) =  \frac{h \cdot h}{h^2+h^2} = \dfrac{h^2}{2h^2} = \dfrac{1}{2} \) mentre \( f(0,0) = 0 \):

\[ D_{\vec{v}}f(0,0) = \lim_{h \to 0} \frac{\frac{1}{2} - 0}{h} = \lim_{h \to 0} \frac{1}{2h} = \pm \infty \]

Questo limite non esiste perché tende a \( +\infty \) se \( h \to 0^+ \) e a \( -\infty \) se \( h \to 0^- \)

Anche se il limite esiste lungo \( y = 0 \) e \( x= 0 \) e vale \( 0 \), per essere continua deve esistere anche in tutte le altre direzioni.

In questo caso il limite non esiste nel punto (0,0) nella direzione y=x, quindi la funzione non è continua in \( (0,0) \).

Quindi non è differenziabile nel punto in questione.

Nota. Per dimostrare la non continuità della funzione \( \frac{xy}{x^2 + y^2} \) nel punto (0,0) bastava osservare che la funzione assume valori diversi a seconda della direzione di avvicinamento. Lungo l'asse x (cioé y=0) la funzione vale f(x,y)=0. \[   \lim_{x\to0} f(x,0)= \lim_{x\to0} \frac{x \cdot 0}{x^2 + 0^2} =   0   \] Lungo la retta y=x, invece, la funzione vale f(x,x)=1/2. \[   \lim_{x\to0} f(x,x)= \lim_{x\to0} \frac{x \cdot x}{x^2 + x^2} = \lim_{x\to0} \frac{x^2}{2x^2} = \lim_{x\to0} \frac{1}{2} = \tfrac12   \] Questo basta per affermare che la funzione non è continua nel punto (0,0).

Riepilogando, la funzione ha tutte le derivate parziali in \( (0,0) \), ma il suo comportamento cambia a seconda della direzione da cui mi avvicino.

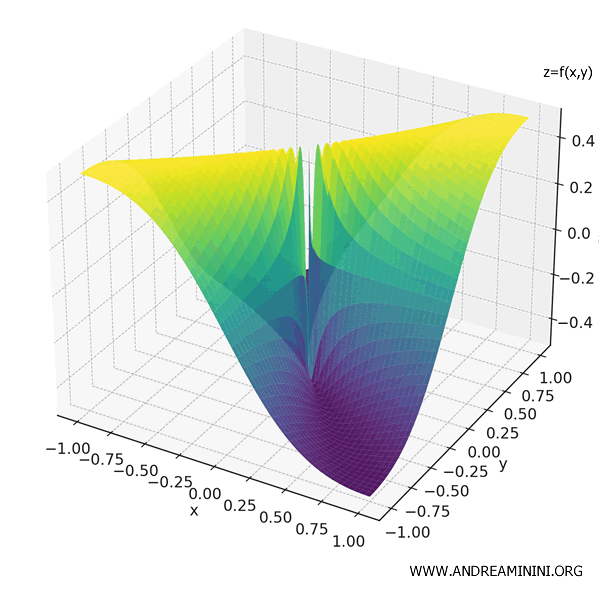
Questo è un classico esempio di funzione che ha tutte le derivate parziali in un punto, esistono e sono nulle, ma la funzione non è continua, né differenziabile in quel punto.

Dimostra che l'inverso del teorema della differenziabilità non vale.

Esempio 2

In questo esempio studio la funzione di due variabili

\[ f(x,y) =  \begin{cases} \left( \frac{x^2 y}{x^4 + y^2} \right)^2 & \text{se } (x,y) \neq (0,0) \\ 0 & \text{se } (x,y) = (0,0)
\end{cases} \]

Per capire se \(f\) è continua in \((0,0)\), devo vedere se:

\[ \lim_{(x,y) \to (0,0)} f(x,y) = f(0,0) = 0 \]

Ma se mi avvicino a \((0,0)\) lungo la parabola \(y = x^2\), ossia ponendo \( x = t, \quad y = t^2 \) ottengo:

\[ f(t, t^2) = \left( \frac{t^2 \cdot t^2}{t^4 + t^4} \right)^2 = \left( \frac{t^4}{2t^4} \right)^2 = \left( \frac{1}{2} \right)^2 = \frac{1}{4}  \]

Quindi il limite lungo questa direzione vale 1/4, mentre \(f(0,0) = 0\).

Se il limite dipende dalla direzione che scelgo... allora il limite non esiste, pertanto la funzione non è continua in (0,0).

Ora verifico se esistono e quali sono le derivate direzionali in (0,0).

La derivata direzionale lungo un generico vettore \(\vec{v} = (\alpha, \beta)\) in \((0,0)\) si calcola con:

\[ \lim_{t \to 0} \frac{f(0 + t\alpha, 0 + t\beta) - f(0,0)}{t} = \lim_{t \to 0} \frac{f(t\alpha, t\beta)}{t} \]

Ora calcolo:

\[ f(t\alpha, t\beta) = \left( \frac{(t\alpha)^2 \cdot t\beta}{(t\alpha)^4 + (t\beta)^2} \right)^2 = \left( \frac{t^3 \alpha^2 \beta}{t^4 \alpha^4 + t^2 \beta^2} \right)^2. \]

Quindi:

\[
\begin{aligned}
\frac{f(t\alpha,t\beta)}{t}
&=\frac1t\left(
\frac{t^{3}\alpha^{2}\beta}{t^{4}\alpha^{4}+t^{2}\beta^{2}}
\right)^{2}\\[6pt]
&=\frac1t\left(
\frac{t\,\alpha^{2}\beta}{t^{2}\alpha^{4}+\beta^{2}}
\right)^{2}\\[6pt]
&=\frac1t\,
\frac{t^{2}\alpha^{4}\beta^{2}}
{(t^{2}\alpha^{4}+\beta^{2})^{2}}\\[6pt]
&=\frac{t\,\alpha^{4}\beta^{2}}
{(t^{2}\alpha^{4}+\beta^{2})^{2}}.
\end{aligned}
\]

Ora, quando \(t \to 0\), il numeratore va a zero come \(t\), mentre il denominatore tende a \(\beta^2\). Quindi tutto tende a 0.

\[ \lim_{t \to 0} \frac{f(t\alpha, t\beta)}{t} = \lim_{t \to 0} \frac{t\,\alpha^{4}\beta^{2}}{(t^{2}\alpha^{4}+\beta^{2})^{2}} = 0 \]

Pertanto, tutte le derivate direzionali in \((0,0)\) esistono e valgono 0.

In questo caso tutte le derivate direzionali in \((0,0)\) esistono e sono nulle, ma la funzione non è continua in \((0,0)\).

Quindi la funzione non è derivabile, anche se tutte le derivate direzionali esistono.

In conclusione, avere tutte le derivate direzionali (anche nulle) non basta per avere continuità o derivabilità.

E così via.