Intorno circolare

Nello spazio vettoriale $\mathbb{R^2} = \mathbb{R} \times \mathbb{R}$, un intorno circolare (o disco aperto)  è un cerchio aperto con centro nel punto $(x_0, y_0)$ e raggio positivo $\delta > 0$. $$ I_{\delta} = \{ (x, y) \in \mathbb{R^2} : \sqrt{(x - x_0)^2 + (y - y_0)^2} < \delta \} $$

L'insieme $I_{\delta}$ è un sottoinsieme dello spazio $\mathbb{R^2}$.

Si parla di intorno "aperto" perché non include i punti che si trovano sulla circonferenza di raggio $\delta$ centrata in $(x_0, y_0)$, ma solo i punti al suo interno.

Tutti i punti $(x, y)$ che soddisfano la condizione $\sqrt{(x - x_0)^2 + (y - y_0)^2} < \delta$ fanno parte dell'intorno circolare $I_{\delta}$, sono detti "punti interni" di $I_{\delta}$ e costituiscono il cosiddetto "interno" di $I_{\delta}$. Ad esempio, il punto A.

Al contrario, i punti che non appartengono all'intorno circolare $I_{\delta}$ si trovano all'esterno del cerchio aperto e sono detti  "punti esterni" di $I_{\delta}$. Ad esempio, il punto B.

Questi punti appartengono al complemento dell'intorno  $\overline{I}_{\delta}  = \mathbb{R^2} - I_{\delta} $

I punti $(x, y)$ che si trovano esattamente sulla circonferenza di raggio $\delta$, ovvero quelli per cui $\sqrt{(x - x_0)^2 + (y - y_0)^2} = \delta$, sono detti "punti di frontiera". Questi punti non appartengono all'intorno aperto $I_{\delta}$ e costituiscono la frontiera dell'intorno. Ad esempio, il punto C.

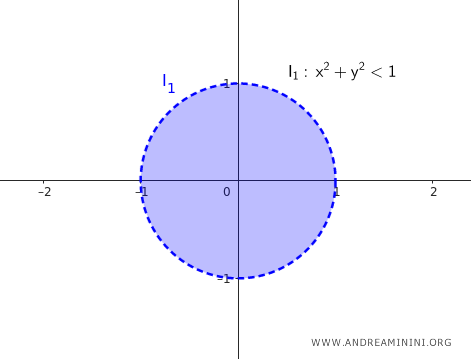
Nota. Se l'intorno circolare è "aperto" non include i punti di confine. Ad esempio, l'intorno circolare del punto (0;0) con raggio $ \delta = 1 $  $$ I_{1 \ aperto} = \{ (x, y) \in \mathbb{R^2} : \sqrt{(x - 0)^2 + (y - 0)^2} < 1 \} $$ In questo caso sono inclusi nell'intorno tutti i punti che hanno una distanza dal centro (0;0) del cerchio minore di $ \delta = 1 $

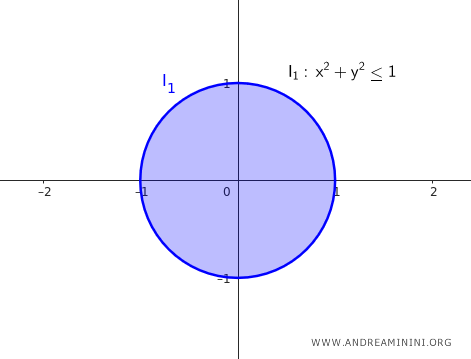
Se invece l'intorno circolare è "chiuso", allora include anche i punti di confine al suo interno $$ I_{1 \ chiuso} = \{ (x, y) \in \mathbb{R^2} : \sqrt{(x - 0)^2 + (y - 0)^2} \le  1 \} $$ In quest'ultimo caso la relazione d'ordine della distanza è "minore-uguale" del raggio $ \delta = 1 $. Quindi, include anche i punti che si trovano sulla circonferenza ossia sul "bordo" del cerchio.

In generale nella topologia standard su $ \mathbb{R^2} $ gli intorni sono sempre insiemi aperti, quindi non includono i punti di confine. Gli insiemi chiusi C, invece, sono il complemento degli insiemi aperti A ossia $ C = \mathbb{R^2} - A $. Pertanto, possono esistere anche insiemi che sono sia aperti che chiusi, i cosiddetti insiemi "clopen". Ad esempio, l'insieme vuoto $ \emptyset $ è l'insieme totale $ \mathbb{R^2} $ sono considerati "aperti" in qualsiasi topologia. Poiché l'uno è il complemento dell'altro ( $ \mathbb{R^2} - \emptyset = \mathbb{R^2} $ e $ \mathbb{R^2} - \mathbb{R^2} = \emptyset $  ) sono anche "chiusi". Quindi, gli insiemi $ \emptyset $ e $ \mathbb{R^2} $ sono sia aperti che chiusi. Sono però concetti un po' difficili da capire per chi si avvicina alla topologia per la prima volta, a cui rimando per qualsiasi approfondimento.

Tutti i punti $ (x,y) $ che per qualsiasi raggio $ \delta $ hanno un intorno circolare che comprende almeno un altro punto di $ I_{\delta} $ diverso da $(x, y)$ sono detti "punti di accumulazione" di $ I_{\delta} $.

Quindi, tutti i punti interni e i punti sulla frontiera di $ I_{\delta} $ sono punti di accumulazione di $ I_{\delta} $.

Ad esempio, il punto A e il punto C sono punti di accumulazione di $ I_{\delta} $ mentre il punto esterno B non lo è.

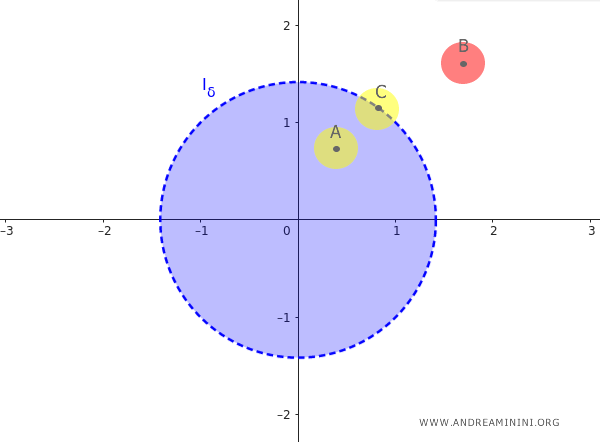
E' opportuno sottolineare che un punto di accumulazione può anche non far parte dell'insieme di riferimento. Ad esempio, il punto di confine C non è un elemento dell'insieme aperto $ I_{\delta} $ ma è comunque un punto di accumulazione di $ I_{\delta} $.

Inoltre, per essere un punto di accumulazione "tutti" gli intorni di un punto (x;y) per qualsiasi raggio $ \delta >0 $ devono comprendere almeno un punto di $ I_{\delta} $ diverso da (x;y).

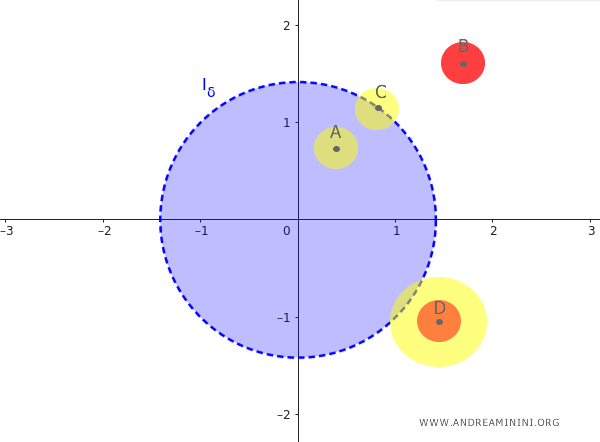
Ad esempio, il punto esterno D ha un intorno circolare opportunamente grande (giallo) che comprende un punto di $ I_{\delta} $ ma questo non vale per qualsiasi raggio $ \delta >0$, ci sono anche intorni di D con raggio inferiore (rosso) che non hanno punti di $ I_{\delta} $ , quindi il punto D non è un punto di accumulazione.

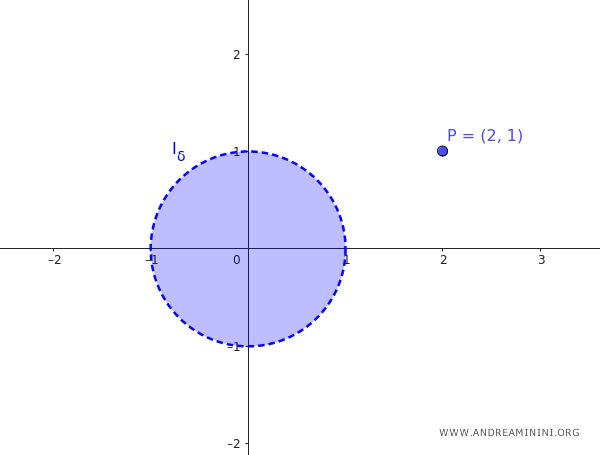
Nota. Se un punto di $ I_{\delta} $ non è un punto di accumulazione, allora è detto "punto isolato" di $ I_{\delta} $. Ad esempio, un insieme $ A $ è composto dall'intorno circolare con centro (0;0) e raggio $ \delta = 1 $ e dal punto P(2;1). $$ A = \{ (x, y) \in \mathbb{R^2} : \sqrt{(x - 0)^2 + (y - 0)^2} < 1 \} \cup \{ P(2;1) \} $$ Il punto P(2;1) è un punto isolato dell'insieme A perché appartiene all'insieme A ma non è un punto di accumulazione di A.

L'unione dei punti dell'intorno circolare $ I_{\delta} $ con i punti di accumulazione di $ I_{\delta} $ è detta "chiusura" dell'insieme $ I_{\delta} $. E' indicata con $ \overline{I}_{\delta} $ oppure $ \text{Cl}(I_{\delta}) $

In altre parole, la chiusura di $ I_{\delta} $ è l'insieme che comprende i punti dell'intorno $ I_{\delta} $ e i suoi punti di confine.

La chiusura di $ I_{\delta} $ è un insieme chiuso.

Nota. La chiusura di $ I_{\delta} $ può essere vista anche come l'intersezione di tutti gli insiemi chiusi che contengono $ I_{\delta} $

Se un intorno A è un insieme aperto, la chiusura di A nello spazio $ \mathbb{R^2} $ è anche detto dominio di $ \mathbb{R^2} $

E così via.