Il metodo della parametrizzazione del bordo di una funzione

Il metodo della parametrizzazione del bordo è una tecnica usata per trovare massimi e minimi assoluti di una funzione di due variabili su un insieme chiuso e limitato.

Quando i punti critici interni non sono sufficienti (o non esistono), bisogna studiare il comportamento della funzione sul bordo dell’insieme.

Tuttavia, sulla frontiera del dominio, non posso applicare il metodo classico dei punti critici (derivate parziali), perché quei punti non sono interni.

Ed è qui che entra in gioco la parametrizzazione.

In cosa consiste?

Supponiamo di avere una funzione $f(x, y)$ definita su un dominio $A$ con bordo curvo o spezzato. Per studiare $f$ sul bordo, seguo questi passaggi:

1. Divido il bordo in tratti più semplici
2. Descrivo ogni tratto con una retta o una curva in forma parametrica: $ (x(t), y(t) ) $ nell'intervallo $ t \in [a, b] $ In questo modo posso percorrere il bordo tramite una funzione di una variabile al variare del parametro $t$.
3. Studio il minimo e il massimo di ogni tratto e individuo così dei punti critici.
4. Analizzo il valore della funzione in questi punti critici, trovando il valore minimo e massimo assoluto della funzione.

Ad esempio, se devo studiare la funzione $f(x, y) = x^2 + y^2$ sul bordo del cerchio $x^2 + y^2 = 1$ parametrizzo il bordo: $$ x(t) = \cos t,\quad t \in [0, 2\pi] $$ $$ y(t) = \sin t,\quad t \in [0, 2\pi] $$ Poi compongo la funzione $$g(t) = f(\cos t, \sin t) =  cos^2 t + \sin^2 t = 1 $$

Un esempio pratico

Considero la funzione di due variabili

$$ f(x,y) = x^2 + 2y $$

sull’insieme chiuso e limitato

$$ A = \{(x,y) \in \mathbb{R}^2 \mid x^2 - 1 \le y \le 3 \} $$

Devo studiare il massimo e il minimo assoluti della funzione

L’insieme $A$ è chiuso e limitato, quindi per il Teorema di Weierstrass esistono il massimo e il minimo assoluto.

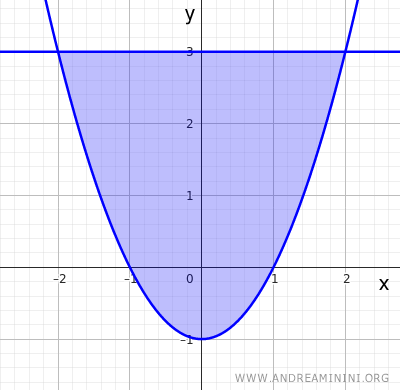
Procedo a cercare il massimo e il minimo nei punti critici interni e sul bordo.

1] Punti critici interni

I punti critici interni sono i punti stazionari, dove la derivata è nulla, e i punti singolari, dove la derivata non esiste.

Calcolo le derivate parziali di x e y:

$$ f_x = 2x $$

$$ f_y = 2 $$

Costruisco un sistema di equazioni per vedere dove si annullano.

$$
\begin{cases}
f_x = 0 \Rightarrow x = 0 \\
f_y = 0 \Rightarrow 2 = 0
\end{cases}
$$

In questo caso il sistema non ha soluzione, quindi non ci sono punti stazionari.

La funzione non ha neanche punti di singolarità.

2] Studio del bordo

Il bordo è composto da un segmento superiore e da una parabola.

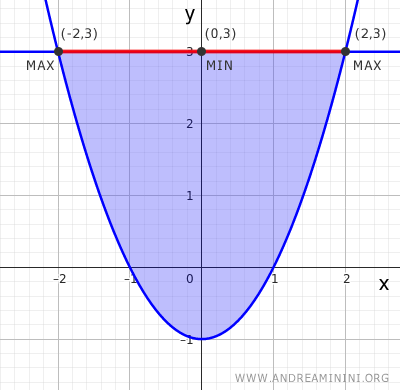
• Bordo 1. Il primo tratto del bordo è un segmento superiore $y = 3$ con $x \in [-2,2]$. Posso parametrizzarlo in questo modo: $(t,3)$, con $t \in [-2,2]$ Sostituisco $ (t,3) $ nella funzione e ottengo $$ g(t) = f(t,3) = t^2 + 2 \cdot 3 = t^2 + 6
  $$ In questo tratto il minimo si ottiene per $$t = 0 \Rightarrow f(0,3) = 6$$ e il massimo per $$t = \pm 2 \Rightarrow f(\pm 2, 3) = 4 + 6 = 10$$ Quindi, questo tratto mi restituisce tre punti candidati:  $(0,3)$, $(-2,3)$, $(2,3)$
  
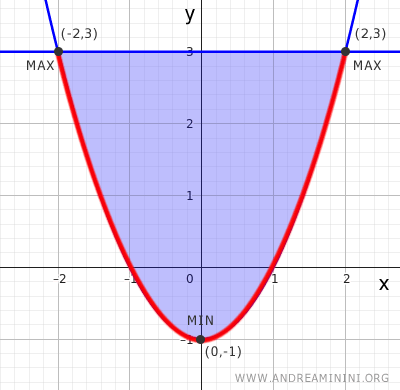
• Bordo 2. Il secondo tratto del bordo è una parabola. $y = x^2 - 1$, con $x \in [-2,2]$ La parametrizzo in questo modo: $(t, t^2 - 1)$, con $t \in [-2,2]$ Poi sostituisco $(t, t^2 - 1)$ nella funzione e ottengo $$ g(t) = f(t, t^2 - 1) = t^2 + 2(t^2 - 1) = 3t^2 - 2 $$ In questo tratto il minimo si ottiene quando $$ t = 0 \Rightarrow f(0, -1) = -2$$ e il massimo quando $$t = \pm 2 \Rightarrow f(\pm 2, 3) = 3 \cdot 4 - 2 = 10$$ Quindi, questo tratto aggiunge altri punti critici: $(0,-1)$, $(-2,3)$, $(2,3)$
  

A questo punto, procedo con la valutazione dei punti candidati.

Calcolo il valore della funzione in ognuno di questi punti critici.

$$
\begin{align*}
f(-2,3) &= 4 + 6 = 10 \\
f(2,3) &= 4 + 6 = 10 \\
f(0,3) &= 0 + 6 = 6 \\
f(0,-1) &= 0 - 2 = -2
\end{align*}
$$

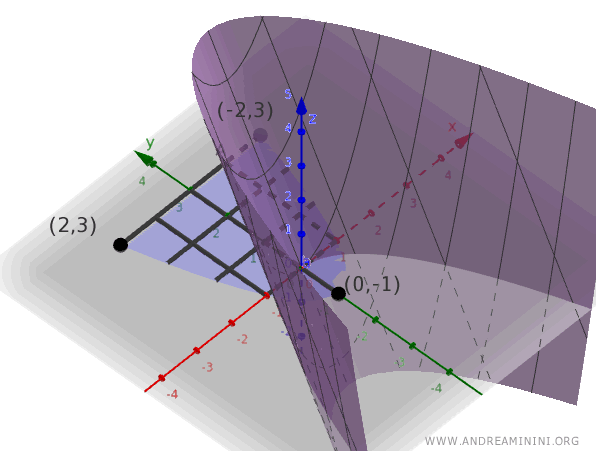
E' evidente che il massimo assoluto $f = 10$ della funzione si registra nei punti $(-2,3)$ e $(2,3)$.

Il minimo assoluto, invece, è $f = -2$ e si ottiene nel punto $(0,-1)$

Come si parametrizzano i tratti del bordo

A seconda della forma del tratto opto per una parametrizzazione specifica.

• Circonferenza
  Per parametrizzare una circonferenza di raggio $ r $ centrata nell'origine scrivo $$ x(t) = r \cos t,\quad y(t) = r \sin t,\quad t \in [0, 2\pi] $$ E se il centro non è l’origine ma $(a, b)$? $$ x(t) = a + r \cos t,\quad y(t) = b + r \sin t $$
• Elisse
  Per parametrizzare una ellisse scrivo $$ x(t) = a \cos t,\quad y(t) = b \sin t,\quad t \in [0, 2\pi] $$ Se poi l’ellisse è spostata: $$ x(t) = x_0 + a \cos t,\quad y(t) = y_0 + b \sin t $$
• Rette (segmenti)
  Per parametrizzare un segmento da $P = (x_1, y_1)$ a $Q = (x_2, y_2)$, scrivo: $$ x(t) = (1 - t)x_1 + t x_2,\quad y(t) = (1 - t)y_1 + t y_2,\quad t \in [0,1] $$
• Iperbole
  Per parametrizzare una iperbole, se ho $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$, posso usare $$ x(t) = a \cosh t,\quad y(t) = b \sinh t,\quad t \in \mathbb{R} $$
• Spirali
  Per parametrizzare la spirale di Archimede scrivo: $$ x(t) = a t \cos t,\quad y(t) = a t \sin t,\quad t \in [0, 2\pi] \text{ o più} $$
• Curve particolari
  Se ho archi o pezzi di funzioni tipo $y = \sqrt{x}$, basta scegliere una variabile $t$ che scorre sull’intervallo giusto e sostituisco $x = t, y = \sqrt{t}$.

In pratica, l’idea è sempre la stessa, prendo il dominio che voglio percorrere, lo faccio variare con un parametro $t$, e scrivo $x(t), y(t)$.

E così via.