Intorno sferico (o Ball)

Un intorno sferico aperto (o "ball" aperta) è l’insieme di tutti i punti che si trovano a distanza minore di un certo valore \( r \) da un punto fissato \( x \). \[ B_r(x) = \{ y \in \mathbb{R}^n : \|y - x\| < r \} \] Dove \( x \) è il centro della ball, \( r > 0 \) è il raggio, mentre \( \|y - x\| \) rappresenta la distanza tra \( y \) e \( x \) (di solito quella euclidea).

L’intorno sferico è chiamato anche "ball" in matematica, è uno degli strumenti fondamentali per capire cosa significa “essere vicino” a un punto in uno spazio.

Può essere "aperta" se non include i confini (bordi) oppure "chiusa" se li include.

È la base per concetti come continuità, convergenza e degli insiemi aperti.

Esempi pratici

Ecco alcuni esempi pratici.

Esempio 1

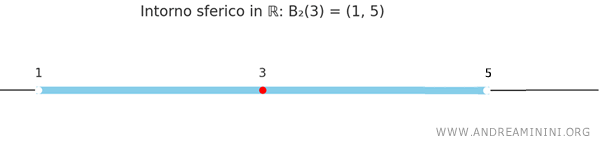
Nello spazio \( \mathbb{R} \) i numeri reali sono rappresentati su una retta di punti e l'intorno sferico si riduce in un intervallo aperto o chiuso.

Ad esempio, se prendo il punto \( x = 3 \) e raggio \( r = 2 \) sulla retta dei numeri reali, l'intervallo è il seguente:

\[ B_2(3) = \{ y \in \mathbb{R} : |y - 3| < 2 \} = (1, 5) \]

È semplicemente l’intervallo aperto centrato in 3, lungo 4 unità totali.

Esempio 2

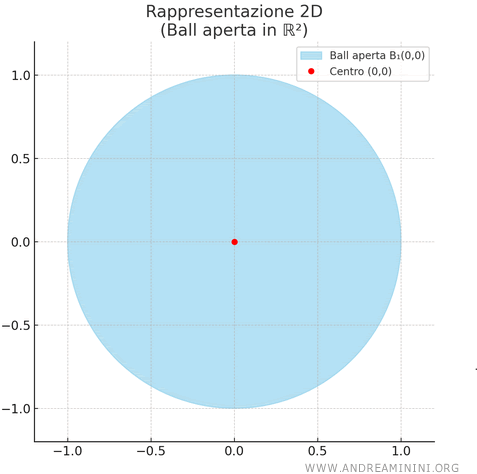
Nel piano \( \mathbb{R}^2 \) la "ball" diventa un disco aperto.

Ad esempio, questo ecco un intorno centrato in (0,0) con raggio 1

\[ B_1((0, 0)) = \{ (x, y) \in \mathbb{R}^2 : \sqrt{x^2 + y^2} < 1 \} \]

Trattandosi di un intorno aperto, quindi il bordo è escluso.

Esempio 3

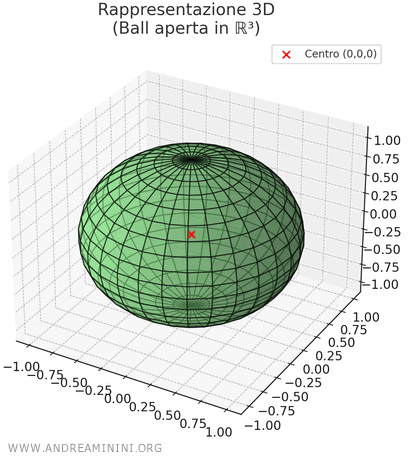
Nello spazio \( \mathbb{R}^3 \) a tre dimensioni una "ball" aperta è una palla senza superficie

\[ B_1((0, 0, 0)) = \{ (x, y, z) \in \mathbb{R}^3 : \sqrt{(x-0)^2 + (y-0)^2 + (z-0)^2} < 1 \} \]

L’interno di una sfera senza superficie esterna.

Poiché è un intorno aperto non include i punti esattamente a distanza \( r=1 \)

L'intorno sferico chiuso (o ball chiusa)

Una ball chiusa include anche il bordo, cioè tutti i punti a distanza minore o uguale a \( r \):

\[ \overline{B}_r(x) = \{ y \in \mathbb{R}^n : \|y - x\| \le r \} \]

In altre parole, l'intorno sferico chiuso comprende la "ball" aperta e il bordo (confine) della sfera.

Esempio

Una ball "chiusa" centrata nell'origine del piano (0,0) con raggio unitario è un disco circolare

\[ \overline{B}_1((0, 0)) = \{ (x, y) \in \mathbb{R}^2 : \sqrt{x^2 + y^2} \le 1 \} \]

In questo caso, il bordo circolare del disco è incluso nell'interno.

Le caratteristiche di un intorno sferico

Le caratteristiche dell'intorno sferico:

• Centrato
  L'intorno sferico è centrato perché ha sempre un punto \( x \) come centro fisso-
• Simmetrico
  L'intorno sferico è simmetrico perché la distanza da \( x \) è ciò che conta, non la direzione
• Topologicamente utile
  L'intorno sferico è topologicamente utile perché serve per definire cosa vuol dire “vicinanza” 

Le tre caratteristiche descritte si ritrovano in tutti gli intorni sferici, aperti o chiusi, indipendentemente dalla dimensione dello spazio.

Le ball negli spazi non euclidei

In matematica, una ball (intorno sferico) può essere definita in qualsiasi spazio metricato, non solo in quello euclideo.

Quando la distanza tra i punti è misurata con una norma diversa dalla norma euclidea, la forma della ball cambia, pur mantenendo la stessa idea: l’insieme di tutti i punti “vicini” a un centro, entro un certo raggio.

In generale, in uno spazio metrico qualsiasi, una ball aperta è definita come:

\[ B_r(x) = \{ y \in X : d(x, y) < r \} \]

Dove \( X \) è lo spazio. \( d(x, y) \) è una distanza generica (non necessariamente euclidea) e  \( r > 0 \) è il raggio.

La forma della ball cambia a seconda della norma o metrica che utilizzo.

Ad esempio, nella distanza euclidea è un cerchio, nella distanza Manhattan è un rombo, ecc.

A] Distanza di Manhattan

Nella distanza Manhattan la ball è definita in questo modo:

\[ \|x - y\|_1 = \sum_{i=1}^n |x_i - y_i| \]

In questo caso la ball in \( \mathbb{R}^2 \) è un rombo (diamante) centrato in \( x \), con i lati inclinati a 45°.

Se il raggio è r=1 diventa

\[ B_1((0,0)) = \{ (x, y) \in \mathbb{R}^2 : |x| + |y| < 1 \} \]

B] Distanza del massimo

Nella distanza del massimo una ball è definita così

\[ \|x - y\|_\infty = \max_i |x_i - y_i| \]

In questo caso la ball in \( \mathbb{R}^2 \) è un quadrato con lati paralleli agli assi, centrato nel punto \( x \).

Ad esempio, se r=1

\[ B_1((0,0)) = \{ (x, y) \in \mathbb{R}^2 : \max(|x|, |y|) < 1 \} \]

C] Spazio con metrica discreta

In uno spazio con metrica discreta la ball si definisce in questo modo:

\[ d(x, y) = \begin{cases} 0 & \text{se } x = y \\ 1 & \text{se } x \ne y \end{cases} \]

In altre parole, se la ball è aperta con raggio 1, contiene solo il punto  \( x \).

Se invece la ball è chiusa contiene tutto lo spazio.

Esempio

Considero uno spazio finito \( X = \{a, b, c\} \) e adotto la metrica discreta, definita così:

\[ d(x, y) =
\begin{cases}
0 & \text{se } x = y \\
1 & \text{se } x \ne y
\end{cases}
\]

Una ball aperta centrata in \( a \) con raggio 1 include solo gli elementi a distanza strettamente minore di 1 da \( a \).  

La distanza è \( d(a, y) < 1 \) solo se \( y = a \), perché per ogni altro elemento \( d(a, y) = 1 \). Quindi, la ball aperta comprende solo l'elemento \( a \).

\[ B_1(a) = \{ a \} \]

La ball chiusa centrata in \( a \), invece, include tutti gli elementi a distanza minore o uguale a 1 da \( a \).  Quindi, tutti gli elementi dello spazio:

\[ \overline{B}_1(a) = \{ y \in X : d(a, y) \le 1 \} = \{a, b, c\} = X \]

Pertanto, in uno spazio con metrica discreta la ball aperta è sempre un singleton (contiene solo il punto centrale) mentre la ball chiusa include tutto lo spazio.

È un esempio estremo, ma è molto utile per capire la differenza tra ball aperta e chiusa anche in contesti non geometrici.

E così via.