Insieme limitato in R² (piano)
Un insieme \( A \) che si trova nel piano cartesiano \( \mathbb{R}^2 \) si dice insieme limitato se esiste un cerchio abbastanza grande con il centro nell'origine (cioè il punto \( (0,0) \)) che riesce a contenere tutto l'insieme \( A \).
Questo significa che esiste un numero \( M > 0 \) tale che, per tutti i punti \( (x,y) \) dell'insieme \( A \), la distanza di questi punti dall'origine calcolata come \( \sqrt{x^2 + y^2} \) è sempre minore o uguale a \( M \).
$$ \sqrt{x^2 + y^2} \le M $$
In altre parole, \( A \) è contenuto in un cerchio di raggio \( M \) centrato nell'origine.
Se riesco a trovare un tale \( M \), allora l'insieme \( A \) è limitato.
Se, invece, non esiste un tale \( M \), allora \( A \) è illimitato.
Un esempio pratico
Considero un insieme di punti nel piano cartesiano, per esempio, un insieme \( A \) formato dai punti \( A = \{ (1, 2), (2, 3), (3, 1), (1, -1) \} \).
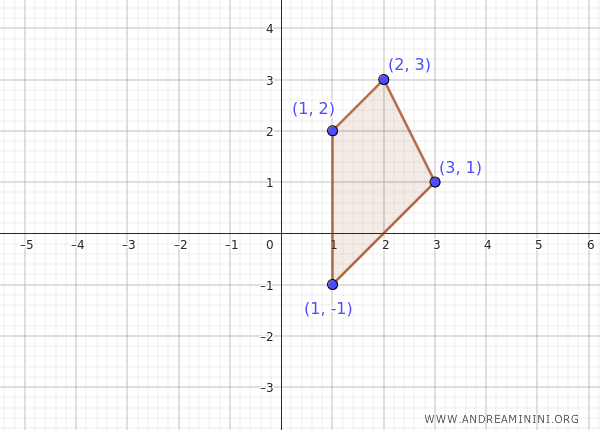
Ora voglio verificare se questo insieme è limitato.
Per farlo, devo vedere se esiste un cerchio con il centro nell'origine che riesca a contenere tutti i punti dell'insieme \( A \).
Calcolo la distanza dall'origine per ogni punto dell'insieme A:
- Per il punto \( (1, 2) \): $$ \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5} \approx 2.24 $$
- Per il punto \( (2, 3) \): $$ \sqrt{2^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13} \approx 3.61 $$
- Per il punto \( (3, 1) \): $$ \sqrt{3^2 + 1^2} = \sqrt{9 + 1} = \sqrt{10} \approx 3.16 $$
- Per il punto \( (1, -1) \): $$ \sqrt{1^2 + (-1)^2} = \sqrt{1 + 1} = \sqrt{2} \approx 1.41 $$
Tra le distanze calcolate, la più grande è \( \sqrt{13} \approx 3.61 \).
Questo significa che tutti i punti dell'insieme \( A \) sono contenuti in un cerchio di raggio \( M = \sqrt{13} \approx 3.61 \) con il centro nell'origine.
$$ \sqrt{ x^2 + y^2 } \le \sqrt{13} $$
Poiché esiste un tale raggio \( M \), posso dire che l'insieme \( A \) è limitato.
In altre parole, posso racchiudere tutti i punti di \( A \) in un cerchio con il centro nell'origine e raggio \( \sqrt{13} \).
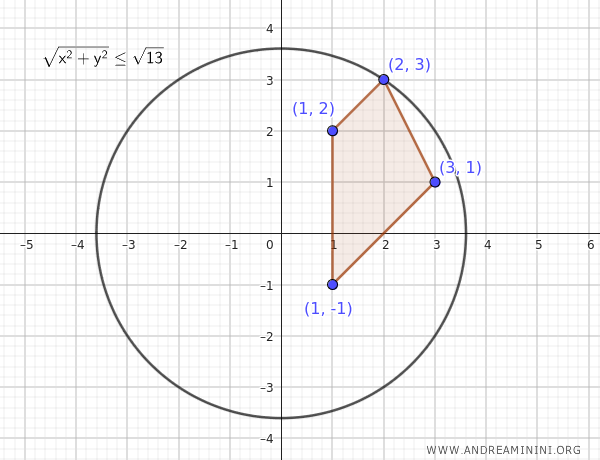
Questo è un esempio pratico che mostra come determinare se un insieme di punti nel piano è limitato o meno.
Nota. Se avessi un insieme con punti che si estendono indefinitamente lontano dall'origine, ad esempio tutti i punti lungo una retta che non passa per l'origine, allora non sarebbe possibile trovare un cerchio che li contenga tutti, e l'insieme sarebbe illimitato.
E così via.
