Il metodo dei moltiplicatori di Lagrange
Il metodo di Lagrange è una tecnica per trovare i punti critici di una funzione di due variabili $ f(x,y) $ quando esistono dei vincoli sulle variabili.
In pratica, invece di cercare l’estremo in tutto il piano, lo cerco solo sui punti che rispettano il vincolo.
Questo mi permette di trovare estremi vincolati senza dover parametrizzare i vincoli.
Come funziona?
Data una funzione $ f(x, y) $ soggetta al vincolo $ g(x, y) = 0 $, costruisco una nuova funzione chiamata lagrangiana:
$$ L(x, y, \lambda) = f(x, y) + \lambda g(x, y) $$
Dove il parametro $ \lambda $ è detto moltiplicatore di Lagrange.
Per trovare i punti critici della lagrangiana, è necessario che tutte le derivate parziali della lagrangiana siano nulle. Quindi, costruisco il sistema di equazioni:
$$
\begin{cases}
f_x(x,y) + \lambda g_x(x,y) = 0 \\
f_y(x,y) + \lambda g_y(x,y) = 0 \\
g(x, y) = 0
\end{cases}
$$
Dove $ f_x(x,y) = \frac{\partial f}{\partial x} $ è la derivata parziale di $ f $ rispetto a $ x $, mentre $ f_y(x,y) = \frac{\partial f}{\partial y} $ è la derivata parziale di $ f $ rispetto a $ y $.
Il parametro $ \lambda $ è ancora incognito epuò assumere un valore positivo o negativo, quindi il sistema di equazioni può anche essere scritto in questa forma:
$$
\begin{cases}
\frac{\partial f}{\partial x} = \lambda \frac{\partial g}{\partial x} \\
\frac{\partial f}{\partial y} = \lambda \frac{\partial g}{\partial y} \\
g(x, y) = 0
\end{cases}
$$
La soluzione del sistema mi permette di trovare le coordinate dei punti critici $ (x, y) $ sulle curve vincolate in cui la funzione $ f(x, y) $ può assumere un estremo.
Una volta trovati i punti critici devo verificare quali di questi punti critici sono minimi o massimi. Questo si può fare in due modi alternativi:
- Sostituendo le coordinate di ciascun punto critico nella funzione $f(x, y)$ e confrontarne i valori.
- Analizzando la matrice hessiana.
In parole povere, l’uso della lagrangiana traduce il problema in un sistema risolvibile con il calcolo differenziale.
Nota. Il metodo richiede che il vincolo della funzione sia sempre espresso nella forma $ g(x,y)=0 $.
Un esempio pratico
Considero la funzione di due variabili
$$ f(x, y) = 3x + 4y $$
Entro il vincolo dei punti di una circonferenza
$$ x^2 + y^2 = 25 $$
Poiché il metodo dei moltiplicatori di Lagrange richiede che il vincolo sia scritto nella forma $ g(x,y)=0 $, trasformo il vincolo in questo modo:
$$ g(x,y): x^2 + y^2 - 25 = 0 $$
Per trovare il minimo e il massimo della funzione devo cercare i punti della circonferenza $ x^2 + y^2 - 25 = 0 $ in cui la funzione $ f(x, y) = 3x + 4y $ è stazionaria.
Come primo passo costruisco la lagrangiana:
$$ L(x, y, \lambda) = 3x + 4y + \lambda(x^2 + y^2 - 25) $$
Poi calcolo le derivate parziali e le eguaglio a zero
$$ \frac{\partial L}{\partial x} = 3 + 2\lambda x = 0 $$
$$ \frac{\partial L}{\partial y} = 4 + 2\lambda y = 0 $$
Quindi, costruisco il sistema di equazioni:
$$ \begin{cases}
3 + 2\lambda x = 0 \\
4 + 2\lambda y = 0 \\
x^2 + y^2 = 25
\end{cases}
$$
Poi risolvo il sistema.
Dalla prima equazione ricavo: $ \lambda = -\frac{3}{2x} $
$$ \begin{cases}
\lambda = -\frac{3}{2x} \\
4 + 2\lambda y = 0 \\
x^2 + y^2 = 25
\end{cases}
$$
Dalla seconda equazione ottengo: $ \lambda = -\frac{2}{y} $
$$ \begin{cases}
\lambda = -\frac{3}{2x} \\
\lambda = -\frac{2}{y} \\
x^2 + y^2 = 25
\end{cases}
$$
Uguaglio le due espressioni:
$$ -\frac{3}{2x} = -\frac{2}{y} \quad \Rightarrow \quad \frac{3}{2x} = \frac{2}{y} \Rightarrow 3y = 4x \Rightarrow y = \frac{4}{3}x
$$
A questo punto sostituisco il risultato $ y = \frac{4}{3}x $ nella circonferenza:
$$ x^2 + \left(\frac{4}{3}x\right)^2 = 25 $$
$$ x^2 + \frac{16}{9}x^2 = 25 $$
$$ \frac{25}{9}x^2 = 25 $$
$$ x^2 = 9 $$
$$ x = \pm 3 $$
Se $x = 3 $, $y = 4 $ mentre se $x = -3 $, $y = -4 $
Pertanto, i punti stazionari da verificare sono $ P_1 = (3, 4) $ e $P_2 = (-3, -4) $.
Infine, sostituisco queste coordinate nella funzione $ f(x, y) = 3x + 4y $ per ottenere i valori:
$$ f(3, 4) = 3 \cdot 3 + 4 \cdot 4 = 9 + 16 = 25 $$
$$ f(-3, -4) = -9 -16 = -25 $$
Quindi, il punto $ P_1 = (3, 4) $ è il massimo della funzione ( $ f(3,4)=25 $ ) mentre il punto $P_2 = (-3, -4) $ è il minimo ( $ f(-3,-4)=-25 $ ) entro il vincolo indicato.
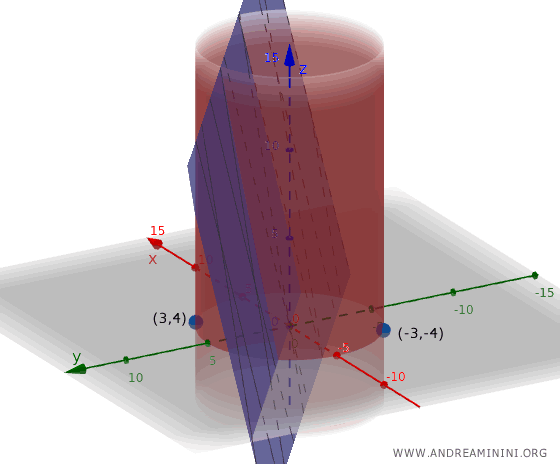
Ho così trovato i punti della circonferenza in cui la funzione $f(x, y) $ raggiunge il massimo e il minimo, usando solo equazioni e derivate, senza bisogno di disegnare la curva.
Il calcolo della matrice hessiana
Per verificare quale dei punti critici $ (3, 4) $ e $(-3, -4) $ è il massimo o il minimo avrei potuto usare anche la matrice hessiana estesa che incorpora anche il vincolo.
$$
H_L =
\begin{pmatrix}
L_{xx} & L_{xy} & g_x \\
L_{yx} & L_{yy} & g_y \\
g_x & g_y & 0
\end{pmatrix}
$$
Dove:
- $L_{xx} = \frac{\partial^2 L}{\partial x^2} = f_{xx} + \lambda g_{xx}$, e così via per gli altri.
- $g_x = \frac{\partial g}{\partial x}$
Nota. La matrice hessiana estesa si distingue dalla matrice hessiana classica. La matrice Hessiana classica serve a studiare la natura dei punti critici di una funzione libera, analizzando solo le derivate seconde di f(x,y). $$ H = \begin{pmatrix}
\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
\frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2}
\end{pmatrix} $$ La matrice Hessiana estesa, invece, si usa nei problemi con vincoli, perché incorpora anche le derivate seconde del vincolo e le sue derivate prime, legandole alla lagrangiana. $$
H_L =
\begin{pmatrix}
L_{xx} & L_{xy} & g_x \\
L_{yx} & L_{yy} & g_y \\
g_x & g_y & 0
\end{pmatrix}
$$
In questo caso devo calcolare anche le derivate parziali seconde della lagrangiana $ L(x, y, \lambda) = 3x + 4y + \lambda(x^2 + y^2 - 25) $ e del vincolo $ g(x,y)= x^2 + y^2 - 25 $
$$ L_{xx} = 2 \lambda $$
$$ L_{xy} = 0 $$
$$ L_{yy} = 2 \lambda $$
$$ L_{yx} = 0 $$
$$ g_{xx} = 2 $$
$$ g_{xy} = 0 $$
$$ g_{yy} = 2 $$
$$ g_x = 2x $$
$$ g_y = 2y $$
Sostituisco le derivate seconde nella matrice hessiana.
$$ H_L = \begin{array}{ccc}
2\lambda & 0 & 2x \\
0 & 2\lambda & 2y \\
2x & 2y & 0
\end{array} $$
A questo punto sostituisco le coordinate dei punti critici per ottenere il valore di $ \lambda $.
Poi calcolo il determinante e verifico se è positivo o negativo. Se è positivo, il punto studiato è un massimo. Viceversa, se è negativo è un minimo.
1] Punto critico (3,4)
Calcolo $ \lambda $ usando:
$$ 3 + 2\lambda x = 0 \Rightarrow 3 + 2\lambda \cdot 3 = 0 \Rightarrow \lambda = -\frac{1}{2} $$
Poi sostituisco nella matrice hessiana
$$
H_L =
\left|
\begin{array}{ccc}
-1 & 0 & 6 \\
0 & -1 & 8 \\
6 & 8 & 0
\end{array}
\right|
$$
Calcolo il determinante sviluppando la prima riga:
$$ \Delta H_L =
-1 \cdot
\left|
\begin{array}{cc}
-1 & 8 \\
8 & 0
\end{array}
\right|
+ 0 - 6 \cdot
\left|
\begin{array}{cc}
0 & -1 \\
6 & 8
\end{array}
\right|
$$
$$ \Delta H_L = -1(-1 \cdot 0 - 8 \cdot 8) - 6(0 \cdot 8 - (-1)\cdot 6) $$
$$ \Delta H_L = -1( -64 ) - 6(6) = 64 - 36 = 28 $$
Il risultato è positivo, quindi $(3, 4) $ è un massimo relativo vincolato.
2] Punto critico (-3,-4)
Trovo $ \lambda $ usando le coordinate del punto
$$ 3 + 2\lambda (-3) = 0 \Rightarrow \lambda = \frac{1}{2} $$
Sostituisco $ \lambda = \frac{1}{2} $ nella matrice hessiana:
$$
H_L =
\left|
\begin{array}{ccc}
1 & 0 & -6 \\
0 & 1 & -8 \\
-6 & -8 & 0
\end{array}
\right|
$$
Poi calcolo il determinante sviluppando la prima riga
$$ \Delta H_L = 1 \cdot
\left|
\begin{array}{cc}
1 & -8 \\
-8 & 0
\end{array}
\right|
- 0 + (-6) \cdot
\left|
\begin{array}{cc}
0 & 1 \\
-6 & -8
\end{array}
\right|
$$
$$ \Delta H_L = 1(0 - (-8)(-8)) - 6(0 \cdot (-8) - 1 \cdot (-6)) $$
$$ \Delta H_L = 1(-64) - 6(6) = -64 - 36 = -100 $$
Il risultato è negativo, quindi $(-3, -4) $ è un minimo relativo vincolato.
La verifica con la matrice Hessiana conferma perfettamente i risultati ottenuti col confronto diretto dei valori.
Esempio 2
Devo trovare il minimo e il massimo della funzione
$$ f(x,y) = x-2y $$
nel vincolo di una circonferenza
$$ g(x,y) = \{(x,y) \in R^2 : x^2+y^2 \le 3 $$
Riscrivo il vincolo nella forma $ g(x,y)=0 $
$$ x^2+y^2 - 3 = 0 $$
Procedo analizzando il bordo dell'insieme.
Per trovare i punti candati in cui cercare il minimo e il massimo provo prima a risolvere il sistema di equazioni.
$$ \begin{cases} g_x(x,y) = 0 \\ g_y(x,y) = 0 \\ g(x,y)=0 \end{cases} $$
$$ \begin{cases} 2x = 0 \\ 2y = 0 \\ x^2+y^2 - 3=0 \end{cases} $$
$$ \begin{cases} x = 0 \\ y = 0 \\ x^2+y^2=3 \end{cases} $$
Il sistema non ha soluzioni.
Quindi, cerco i punti candidati anche risolvendo il secondi sistema.
$$ \begin{cases} f_x(x,y) = \lambda \cdot g_x(x,y) \\ f_y(x,y) = \lambda \cdot g_y(x,y) \\ g(x,y)=0 \end{cases} $$
$$ \begin{cases} 1 = 2 \lambda x \\ -2 = 2 \lambda y \\ x^2+y^2 - 3=0 \end{cases} $$
$$ \begin{cases} x = \frac{1}{2 \lambda} \\ y = - \frac{1}{ \lambda } \\ x^2+y^2 - 3=0 \end{cases} $$
$$ \begin{cases} x = \frac{1}{2 \lambda} \\ y = - \frac{1}{ \lambda } \\ ( \frac{1}{2 \lambda} )^2+( - \frac{1}{ \lambda } )^2 =3 \end{cases} $$
$$ \begin{cases} x = \frac{1}{2 \lambda} \\ y = - \frac{1}{ \lambda } \\ \frac{1}{4 \lambda^2} + \frac{1}{ \lambda^2 } =3 \end{cases} $$
$$ \begin{cases} x = \frac{1}{2 \lambda} \\ y = - \frac{1}{ \lambda } \\ \frac{5}{4 \lambda^2} =3 \end{cases} $$
$$ \begin{cases} x = \frac{1}{2 \lambda} \\ y = - \frac{1}{ \lambda } \\ \lambda^2 = \frac{5}{12} \end{cases} $$
$$ \begin{cases} x = \frac{1}{2 \lambda} \\ y = - \frac{1}{ \lambda } \\ \lambda = \pm \frac{\sqrt{5}}{ \sqrt{12}} \end{cases} $$
$$ \begin{cases} x = \frac{1}{2 \lambda} \\ y = - \frac{1}{ \lambda } \\ \lambda = \pm \frac{\sqrt{5}}{ 2\sqrt{3}} \end{cases} $$
Una volta trovati i valori di $ \lambda = \pm \frac{\sqrt{5}}{ 2\sqrt{3}} $ li sostituisco nelle prime due equazioni per trovare le coordinate dei punti (x,y)
Se $ \lambda = \frac{\sqrt{5}}{ 2\sqrt{3}} $
$$ x = \frac{1}{2 \lambda} $$
$$ x = \frac{1}{2 \frac{\sqrt{5}}{ 2\sqrt{3}}} $$
$$ x = \frac{1}{\frac{\sqrt{5}}{ \sqrt{3}}} $$
$$ x = \frac{ \sqrt{3} }{ \sqrt{5}} $$
$$ y = - \frac{1}{ \lambda } $$
$$ y = - \frac{1}{ \frac{\sqrt{5}}{ 2\sqrt{3}} } $$
$$ y = - \frac{ 2\sqrt{3} }{ \sqrt{5}} $$
Quindi, il primo punto candidato è $ (x;y)= ( \frac{ \sqrt{3} }{ \sqrt{5}} ; - \frac{ 2\sqrt{3} }{ \sqrt{5}} ) $
Se $ \lambda = - \frac{\sqrt{5}}{ 2\sqrt{3}} $
$$ x = \frac{1}{2 \lambda} $$
$$ x = \frac{1}{2 (- \frac{\sqrt{5}}{ 2\sqrt{3}} ) } $$
$$ x = - \frac{1}{\frac{\sqrt{5}}{ \sqrt{3}}} $$
$$ x = - \frac{ \sqrt{3} }{ \sqrt{5}} $$
$$ y = - \frac{1}{ \lambda } $$
$$ y = - \frac{1}{ - \frac{\sqrt{5}}{ 2\sqrt{3}} } $$
$$ y = \frac{ 2\sqrt{3} }{ \sqrt{5}} $$
Quindi, il secondo punto candidato è $ (x;y)= ( - \frac{ \sqrt{3} }{ \sqrt{5}} ; \frac{ 2\sqrt{3} }{ \sqrt{5}} ) $
Ora sostituisco le coordinati dei punti (x;y) nella funzione f(x,y) per trovare quale è il valore massimo e quale il minimo
$$ f( \frac{ \sqrt{3} }{ \sqrt{5}} ; - \frac{ 2\sqrt{3} }{ \sqrt{5}}) = \frac{ \sqrt{3} }{ \sqrt{5}} + \frac{ 4\sqrt{3} }{ \sqrt{5}} = \frac{5 \sqrt{3}}{ \sqrt{5} } = \sqrt{15} $$
$$ f( - \frac{ \sqrt{3} }{ \sqrt{5}} ; \frac{ 2\sqrt{3} }{ \sqrt{5}}) = - \frac{ \sqrt{3} }{ \sqrt{5}} - \frac{ 4\sqrt{3} }{ \sqrt{5}} = - \frac{5 \sqrt{3}}{ \sqrt{5} } = - \sqrt{15} $$
E' quindi evidente che il massimo della funzione f(x,y) entro il vincolo g(x,y) si trova alle coordinate $ (x;y)= ( \frac{ \sqrt{3} }{ \sqrt{5}} ; - \frac{ 2\sqrt{3} }{ \sqrt{5}} ) $ mentre il minimo alle coordinate $ (x;y)= ( - \frac{ \sqrt{3} }{ \sqrt{5}} ; \frac{ 2\sqrt{3} }{ \sqrt{5}} ) $
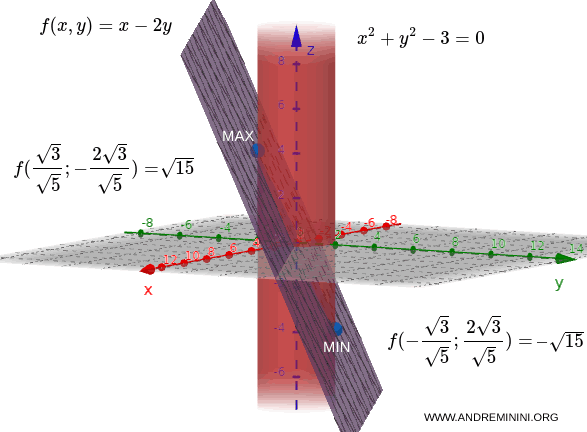
E così via.
