Matrice Hessiana

La matrice Hessiana è una matrice quadrata che contiene tutte le derivate parziali seconde di una funzione: $$ H = \begin{pmatrix}\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\\frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2}\end{pmatrix}$$ Sulla diagonale principale ci sono le derivate seconde pure: due volte rispetto a $x$ e due volte rispetto a $y$. Sulla diagonale secondaria, invece, le derivate miste: prima rispetto a una variabile, poi all’altra.

Questa matrice è molto utile per determinare la natura dei punti critici di una funzione di più variabili.

In particolare, è utilizzata per funzioni di due variabili come $f(x, y)$ per stabilire se un punto critico è un minimo locale, un massimo locale oppure un punto di sella.

Come si usa per studiare i punti critici

Per capire se un punto critico è massimo, minimo o punto di sella:

1. Trovo i punti critici: risolvo il sistema in cui annullo le derivate prime.
2. Costruisco la Hessiana: calcolo le derivate seconde e costruisco la matrice.
3. Valuto la Hessiana nei punti critici: sostituisco i valori delle coordinate.
4. Calcolo il determinante $\Delta$ della matrice Hessiana: $$ \Delta = \left( \frac{\partial^2 f}{\partial x^2} \cdot \frac{\partial^2 f}{\partial y^2} \right) - \left( \frac{\partial^2 f}{\partial x \partial y} \right)^2 $$
5. A seconda del determinante capisco la natura del punto critico
   • Se $\Delta > 0$ e $\frac{\partial^2 f}{\partial x^2} > 0$, è un minimo locale
   • Se $\Delta > 0$ e $\frac{\partial^2 f}{\partial x^2} < 0$, è un massimo locale
   • Se $\Delta < 0$, il punto è un punto di sella
   • Se $\Delta = 0$, la Hessiana non è sufficiente per decidere. Il punto va studiato in modo diverso.

Quindi, con poche operazioni algebriche posso capire dove la funzione raggiunge un massimo, un minimo o si comporta in modo "ambiguo".

Un esempio pratico

Considero la funzione:

$$ f(x, y) = xy $$

Le derivate prime sono:

$$ \frac{\partial f}{\partial x} = y $$

$$ \frac{\partial f}{\partial y} = x $$

Le derivate parziali prime si annullano nel punto $(0,0)$, questo è un punto critico dove può trovarsi un minimo o un massimo della funzione.

Per capirlo posso usare la matrice Hessiana.

Calcolo le derivate parziali seconde della funzione:

$$ \frac{\partial^2 f}{\partial x^2} = 0 $$

$$ \frac{\partial^2 f}{\partial y^2} = 0 $$

$$ \frac{\partial^2 f}{\partial x \partial y} = 1 $$

Poi costruisco la Hessiana:

$$
H = \begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}
$$

In questo caso nella Hessiana non ci sono le variabili $ x $ e $ y $, quindi non devo sostituire le variabili con le coordinate del punto che voglio analizzare $ (0,0) $.

Infine, calcolo il determinante:

$$ \Delta = 0 \cdot 0 - 1 \cdot 1 = -1 $$

Il risultato è un numero negativo, quindi il punto $ (0,0) $ è un punto di sella della funzione.

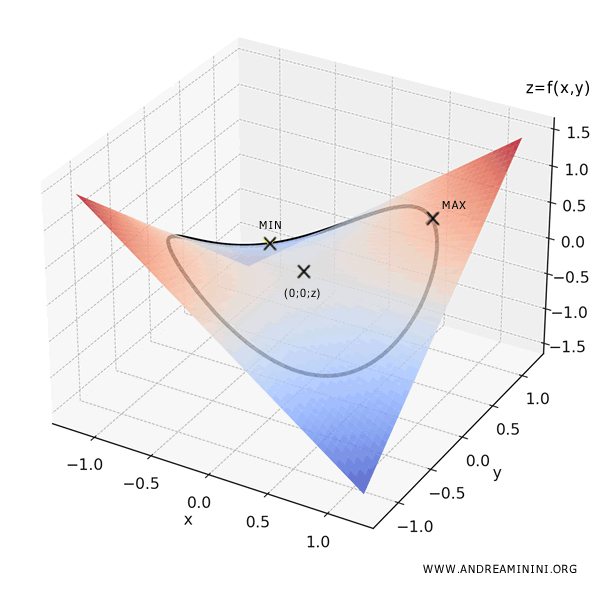
Esempio 2

Considero la funzione:

$$ f(x,y) = x^4 - 2xy + y^4 $$

Le derivate parziali prime della funzione sono:

$$ \frac{\partial f}{\partial x} = 4x^3 - 2y $$

$$ \frac{\partial f}{\partial y} = 4y^3 - 2x $$

Per trovare i punti critici risolvo questo sistema

$$
\begin{cases}
4x^3 - 2y = 0 \\
4y^3 - 2x = 0
\end{cases}
\Rightarrow
\begin{cases}
y = 2x^3 \\
32x^9 - 2x = 0 \Rightarrow x = 0 \text{ o } x = \pm \frac{1}{\sqrt{2}}
\end{cases}
$$

Ottengo tre punti critici:

• $(0,0)$
• $\left( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \right)$
• $\left( -\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}} \right)$

A questo punto costruisco la Hessiana:

Le derivate parziali seconde della funzione sono:

$$ \frac{\partial^2 f}{\partial x^2} = 12x^2 $$

$$ \frac{\partial^2 f}{\partial y^2} = 12y^2 $$

$$ \frac{\partial^2 f}{\partial x \partial y} = -2 $$

Quindi, la matrice Hessiana è:

$$
H = \begin{pmatrix}
12x^2 & -2 \\
-2 & 12y^2
\end{pmatrix}
$$

Una volta costruita la Hessiana, la utilizzo per verificare la natura di ogni punto critico

• Punto (0,0):
  Sostituisco le coordinate del punto $ x=0 $ e $ y=0 $ nella matrice e calcolo il determinante $$ H = \begin{pmatrix} 0 & -2 \\ -2 & 0 \end{pmatrix}, \quad \Delta = -4 < 0 $$ Il determinante è negativo, quindi è un punto di sella.
• Punto $\left( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \right)$:
  Sostituisco le coordinate del punto nella matrice e calcolo il determinante $$ H = \begin{pmatrix} 6 & -2 \\ -2 & 6 \end{pmatrix}, \quad \Delta = 36 - 4 = 32 > 0 $$ In questo caso il determinante è positivo $ \Delta > 0 $ e la derivata parziale seconda pura è positiva $ \frac{\partial^2 f}{\partial x^2} = 6 > 0 $ Quindi, si tratta di un minimo locale.
• Punto $\left( -\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}} \right)$
  Sostituisco le coordinate del punto nella matrice e calcolo il determinante $$ H = \begin{pmatrix} 6 & -2 \\ -2 & 6 \end{pmatrix} $$ E' la stessa Hessiana precedente. Quindi, per simmetria, anche questo punto è un minimo locale.

Riepilogando, la funzione ha due minimi nei punti $\left( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \right)$ e $\left( -\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}} \right)$ e un punto di sella nel punto $ (0,0) $.

La matrice Hessiana con dominio vincolato

Quando una funzione ha un vincolo (o più vincoli), il metodo classico della matrice Hessiana non si applica direttamente come nel caso di dominio libero.

In presenza di vincoli espliciti, si utilizza il metodo dei moltiplicatori di Lagrange per trovare i punti critici e poi si verifica la loro natura con una matrice Hessiana estesa.

In questo caso, definisco la funzione lagrangiana $ \mathcal{L} $:

$$ \mathcal{L}(x, y, \lambda) = f(x, y) - \lambda g(x, y) $$

Dove $ f(x,y) $ è la funzione da studiare e $ g(x,y) = 0 $ è il vincolo, ossia l’equazione che descrive il dominio ammesso.

Calcolo le derivate parziali della lagrangiana e le metto a zero:

$$ \begin{cases} \frac{\partial \mathcal{L}}{\partial x} = 0 \\ \frac{\partial \mathcal{L}}{\partial y} = 0 \\ \frac{\partial \mathcal{L}}{\partial \lambda} = 0 \end{cases} \Rightarrow \text{Sistema di Lagrange} $$

Risolvo il sistema per trovare i punti critici vincolati della funzione.

Per verificare se un punto critico vincolato è un massimo o un minimo, costruisco la matrice Hessiana estesa, che incorpora anche le derivate del vincolo:

$$ H_L = \begin{pmatrix} \frac{\partial^2 \mathcal{L}}{\partial x^2} & \frac{\partial^2 \mathcal{L}}{\partial x \partial y} & \frac{\partial g}{\partial x} \\ \frac{\partial^2 \mathcal{L}}{\partial y \partial x} & \frac{\partial^2 \mathcal{L}}{\partial y^2} & \frac{\partial g}{\partial y} \\ \frac{\partial g}{\partial x} & \frac{\partial g}{\partial y} & 0 \end{pmatrix} $$

Questa matrice è detta Hessiana estesa perché considera sia la curvatura della funzione, sia la direzione imposta dal vincolo.

È l’unica forma che consente di stabilire con certezza la natura del punto critico sotto vincolo.

Nota. A volte si parla della Hessiana della lagrangiana: $$ H = \begin{pmatrix} \frac{\partial^2 \mathcal{L}}{\partial x^2} & \frac{\partial^2 \mathcal{L}}{\partial x \partial y} \\ \frac{\partial^2 \mathcal{L}}{\partial y \partial x} & \frac{\partial^2 \mathcal{L}}{\partial y^2} \end{pmatrix} $$ Ma questa da sola non basta: non tiene conto delle direzioni lungo cui ci si muove a causa del vincolo. Solo l’Hessiana estesa fornisce una verifica completa.

Una volta costruita la matrice $H_L$, la valuto nel punto critico, calcolo il determinante e verifico il segno:

• Se il determinante è positivo, il punto è un massimo vincolato.
• Se è negativo, ho un minimo vincolato.
• Se è nullo, la verifica è inconcludente e servono altri strumenti.

Esempio di matrice hessiana con dominio vincolalto

Voglio studiare la funzione:

$$ f(x, y) = 3x + 4y $$

sul bordo della circonferenza:

$$ x^2 + y^2 = 25 $$

Scriviamo il vincolo in forma canonica $ g(x,y)=0 $

$$ g(x, y) = x^2 + y^2 - 25 = 0 $$

Poi costruisco la funzione lagrangiana $ L(x,y, \lambda) = f(x,y) + \lambda \cdot g(x,y) $:

$$ L(x, y, \lambda) = 3x + 4y + \lambda(x^2 + y^2 - 25) $$

Calcolo le derivate parziali della lagrangiana rispetto a $x$, $y$ e $\lambda$ e le metto uguali a zero:

$$ \begin{cases}
\frac{\partial L}{\partial x} = 3 + 2\lambda x = 0 \\
\frac{\partial L}{\partial y} = 4 + 2\lambda y = 0 \\
g(x,y) = x^2 + y^2 = 25
\end{cases}
$$

A questo punto risolvo il sistema.

$$ \begin{cases}
3 + 2\lambda x = 0 \\
4 + 2\lambda y = 0 \\
x^2 + y^2 = 25
\end{cases}
$$

Dalla prima equazione ricavo:

$$ \lambda = -\frac{3}{2x} $$

Dalla seconda equazione:

$$ \lambda = -\frac{2}{y} $$

Uguaglio le due espressioni:

$$ \frac{3}{2x} = \frac{2}{y} \Rightarrow 3y = 4x \Rightarrow y = \frac{4}{3}x $$

Sostitusco i valori nella circonferenza:

$$ x^2 + \left( \frac{4}{3}x \right)^2 = 25 \Rightarrow x^2 + \frac{16}{9}x^2 = 25 \Rightarrow \frac{25}{9}x^2 = 25 \Rightarrow x^2 = 9 \Rightarrow x = \pm 3 $$

Pertanto, se $x = 3$, $y = 4$ mentre se $x = -3$, $y = -4$

I punti critici da analizzare sono:

• $ P_1 = (3, 4) $
• $ P_2 = (-3, -4) $

Valuto i punti critici nella funzione:

• $f(3, 4) = 3 \cdot 3 + 4 \cdot 4 = 9 + 16 = 25$
• $f(-3, -4) = -9 - 16 = -25$

Quindi, come conclusione preliminare deduco che

• $P_1 = (3,4)$: massimo relativo vincolato
• $P_2 = (-3,-4)$: minimo relativo vincolato

Per verificare la natura dei punti costruisco la matrice Hessiana estesa

$$
H_L =
\begin{pmatrix}
L_{xx} & L_{xy} & g_x \\
L_{yx} & L_{yy} & g_y \\
g_x & g_y & 0
\end{pmatrix}
$$

Calcolo le derivate:

$$ L_{xx} = 2\lambda $$

$$ L_{yy} = 2\lambda $$

$$ L_{xy} = 0 $$

$$ L_{yx} = 0 $$

$$ g_x = 2x $$

$$ g_y = 2y $$

Quindi, la matrice hessiana estesa è

$$
H_L =
\begin{pmatrix}
2\lambda & 0 & 2x \\
0 & 2\lambda & 2y \\
2x & 2y & 0
\end{pmatrix}
$$

Analizzo ogni singolo punto critico con la matrice hessiana estesa.

• Punto $P_1 = (3, 4)$
  In questo punto $ x=3 $, $ y=4 $ e $\lambda = -\frac{1}{2}$ (da $3 + 2\lambda \cdot 3 = 0$) Quindi, la matrice hessiana estesa diventa: $$ H_L =
  \begin{pmatrix}
  -1 & 0 & 6 \\
  0 & -1 & 8 \\
  6 & 8 & 0
  \end{pmatrix}
  $$ Il determinante della matrice è $$ \Delta = -1 \cdot (0 - 64) - 6 \cdot (0 - 6) = 64 - 36 = 28 > 0 $$ Il determinante è positivo, quindi il punto è un massimo vincolato.
• Punto $P_2 = (-3, -4)$
  In questo punto $ x=3 $, $ y=4 $ e $\lambda = \frac{1}{2}$ (da $3 + 2\lambda \cdot (-3) = 0$) La matrice hessiana estesa diventa: $$
  H_L =
  \begin{pmatrix}
  1 & 0 & -6 \\
  0 & 1 & -8 \\
  -6 & -8 & 0
  \end{pmatrix}
  $$ Il determinante della matrice è $$ \Delta = 1 \cdot (0 - 64) - 6 \cdot (0 - 6) = -64 - 36 = -100 < 0 $$ Il determinante è negativo, quindi il punto è un minimo vincolato.

Sia il metodo diretto, sia la verifica con la matrice Hessiana vincolata portano allo stesso risultato:

• Il massimo della funzione si ottiene in $P_1 = (3,4)$
• Il minimo si ottiene in $P_2 = (-3, -4)$

La matrice Hessiana vincolata consente una verifica rigorosa, utile soprattutto nei casi in cui la funzione non sia lineare e non basti confrontare i valori di $f(x,y)$.

E così via.