Derivata direzionale

La derivata direzionale è la derivata di una funzione \( f \) nel punto \( (x_0, y_0) \) nella direzione del vettore \( \vec{v} = (\alpha, \beta) \)  \[ \frac{\partial f}{\partial \vec{v}}(x_0,y_0) = \lim_{t \to 0} \frac{f(x_0 + t\alpha, \; y_0 + t\beta) - f(x_0, y_0)}{t}  \]

In altre parole, prendo un piccolo passo \( t \) nella direzione di \( \vec{v} \), calcolo quanto cambia la funzione \( f \), e poi divido per la lunghezza del passo.

Questo limite esiste se e solo se il risultato è reale e finito.

Una derivata direzionale è un'estensione della derivata parziale che, invece, si calcola rispetto a un asse di riferimento.

Infatti, se scelgo come direzione il vettore \( \vec{v} = (1,0) \) o \( (0,1) \), cioè lungo gli assi x o y, la derivata direzionale torna ad essere proprio la derivata parziale.

Nota. Una funzione di due variabili genera un grafico tridimensionale. Ad esempio, se il grafico ha la forma di una "collina" e un punto \( (x_0, y_0) \) del piano si trova ai bordi della collina, a seconda della direzione del vettore \( \vec{v} \) in cui mi voglio muovere (non solo quelle degli assi x e y ma anche in diagonale o qualsiasi altra direzione) la derivata direzionale mi restituisce la pendenza, ossia mi dice quanto rapidamente sto salendo o scendendo lungo quella direzione specifica.

Geometricamente la derivata direzionale corrisponde a un movimento lungo la retta di equazione parametrica \( (x_0 + t\alpha, y_0 + t\beta) \), e rappresenta la variazione della funzione lungo questa traiettoria.

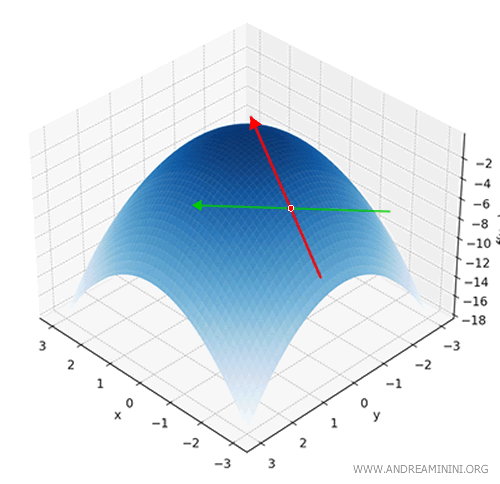
Questo significa che mi sto muovendo lungo una retta che parte da \( (x_0, y_0) \) e vado nella direzione del vettore \( \vec{v} = (\alpha, \beta) \), cioè:

\[ (x(t), y(t)) = (x_0 + t\alpha, \; y_0 + t\beta) \]

La derivata direzionale misura la pendenza della funzione in questa direzione: indica quanto cambia la funzione \( f \).  

In parole povere? È la pendenza della superficie se mi arrampico da quella parte o, nel verso opposto, se rotolo giù.

Nota. In generale, considerando una funzione \( f: \mathbb{R}^n \to \mathbb{R} \) in cui \( \vec{ x_0 } \in \mathbb{R}^n \) è il vettore che rappresenta un punto nello spazio e \( \vec{v} \in \mathbb{R}^n \) è un vettore direzionale non nullo, la derivata direzionale di \( f \) in \( \vec{ x_0 } \) nella direzione di \( \vec{v} \) è definita in notazione vettoriale come: \[ \frac{\partial f}{\partial \vec{v}}( \vec{x}_0 ) = \lim_{t \to 0} \frac{f(\vec{x}_0 + t \vec{v}) - f(\vec{x}_0)}{t} \] Da notare che in questo caso \( \vec{ x_0 } \) non è un numero ma un vettore con le coordinate \( (x_1, x_2, ..., x_n) \) di un punto nello spazio \( \mathbb{R}^n \)

Un esempio pratico

Prendo come esempio la funzione

\[ f(x, y) = x^2 + y^2 \]

Questa funzione genera una superficie a forma di paraboloide (tipo una ciotola), ed è facile da derivare.

Vediamo quanto cresce la funzione \( f(x, y) = x^2 + y^2 \) se mi muovo dal punto \( (1, 2) \) in una direzione precisa, ad esempio nella direzione del vettore \( \vec{v} = (3, 4) \)

Per prima cosa normalizzo la direzione

Per calcolare correttamente la derivata direzionale, il vettore direzione deve essere unitario, cioè di lunghezza 1.

La lunghezza di \( \vec{v} = (3, 4) \) è

\[ \|\vec{v}\| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]

Quindi il vettore unitario è:

\[ \hat{v} = \left(\frac{3}{5}, \frac{4}{5} \right) \]

Poi calcolo il gradiente \( \nabla f(x, y) \) di \( f \) ossia il vettore formato dalle derivate parziali:

\[ \nabla f(x, y) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) = (2x, 2y) \]

Nel punto \( (1, 2) \):

\[ \nabla f(1, 2) = (2 \cdot 1, 2 \cdot 2) = (2, 4) \]

Quindi, calcolo il prodotto scalare tra il gradiente e il vettore unitario \( \hat{v} \):

\[ \frac{\partial f}{\partial \vec{v}}(1, 2) = \nabla f(1, 2) \cdot \hat{v} = (2, 4) \cdot \left( \frac{3}{5}, \frac{4}{5} \right) \]

\[ = \frac{2 \cdot 3 + 4 \cdot 4}{5} = \frac{6 + 16}{5} = \frac{22}{5} \]

In conclusione, la derivata direzionale di \( f(x,y) = x^2 + y^2 \) nel punto \( (1,2) \) nella direzione \( \vec{v} = (3,4) \) è:

\[ \frac{\partial f}{\partial \vec{v}}(1,2) = \frac{22}{5} \]

Questo significa che se mi trovo nel punto \( (1,2) \) sul grafico della funzione \( f(x,y) = x^2 + y^2 \), e mi muovi nella direzione \( (3,4) \), allora la funzione sta aumentando a velocità \( \frac{22}{5} \) in quella direzione.

Il teorema della derivata direzionale

Se la funzione \( f \) è differenziabile in un punto \( \vec{x}_0 \), allora la derivata direzionale di \( f \) lungo una direzione \( \vec{v} \) è uguale al prodotto scalare tra il gradiente di \( f \) in quel punto e il vettore direzione \( \vec{v} \). \[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\nabla}f(x_0) \cdot \vec{v} \] che si può anche scrivere \[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\alpha} \cdot \vec{v} \] dove il gradiente \( \vec{\alpha} = \nabla f(x_0) \) rappresenta la direzione in cui la funzione cresce più rapidamente.

Il prodotto scalare con \( \vec{v} \) misura quanto della variazione di \( f \) segue la direzione \( \vec{v} \).

Se \( \vec{v} \) è ortogonale al gradiente, la derivata direzionale nulla.

Se \( \vec{v} \) è parallela al gradiente, la derivata massima in quella direzione.

Esempio

Considero la funzione

\[ f(x,y) = x^2 + y^2 \]

Prendo come esempio il punto \( \vec x_0 = (1,\,2) \) e come vettore direzione \( \vec v = (3,\,4) \).

Calcolo il gradiente per \(f(x,y)=x^2+y^2\),

\[ \nabla f(x,y) = \bigl(\,\partial_x f,\;\partial_y f\bigr) = (2x,\;2y). \]

Nel punto \(\vec x_0=(1,2)\) diventa:

\[ \nabla f(1,2) = (2\cdot1,\;2\cdot2) = (2,\;4) \]

La derivata direzionale (non unitaria) lungo \(\vec v\) è

\[ \frac{\partial f}{\partial \vec v}(\vec x_0) = \nabla f(\vec x_0)\;\cdot\;\vec v \]

Calcolo il prodotto scalare tra \(\nabla f(1,2)\) e \(\vec v\):

\[ \frac{\partial f}{\partial \vec v}(1,2) = \nabla f(\vec (1,2))\;\cdot\;\vec (3,4) \]

\[ \frac{\partial f}{\partial \vec v}(1,2) = (2,4)\,\cdot\,(3,4) \]

\[ \frac{\partial f}{\partial \vec v}(1,2)  = 2\cdot3 \;+\; 4\cdot4 \]

\[ \frac{\partial f}{\partial \vec v}(1,2) = 6 \;+\; 16  \]

\[ \frac{\partial f}{\partial \vec v}(1,2) = 22 \]

Dove 22 è il tasso di variazione di \(f\) nella direzione \((3,4)\) "non normalizzata".

Per calcolare anche la derivata direzionale unitaria (normalizzata) lungo \(\hat v = \vec v/\|\vec v\|\), calcolo prima la norma \( \|\vec v\| \) del vettore

\[ \|\vec v\| = \sqrt{3^2 + 4^2} = 5, \qquad \hat v = \bigl(\tfrac{3}{5},\,\tfrac{4}{5}\bigr). \]

Quindi, la derivata unitaria lungo questa direzione è:

\[ D_{\hat v}f(1,2) = \nabla f(1,2)\cdot \hat v = (2,4)\cdot\Bigl(\tfrac{3}{5},\tfrac{4}{5}\Bigr) = \frac{1}{5}(2\cdot3 + 4\cdot4)
= \frac{22}{5} = 4.4 \]

Dove 4.4 è il tasso di variazione "per unità di lunghezza" lungo quella stessa direzione.

In questo esempio pratico si vede chiaramente come dal gradiente si ricava immediatamente la derivata direzionale.

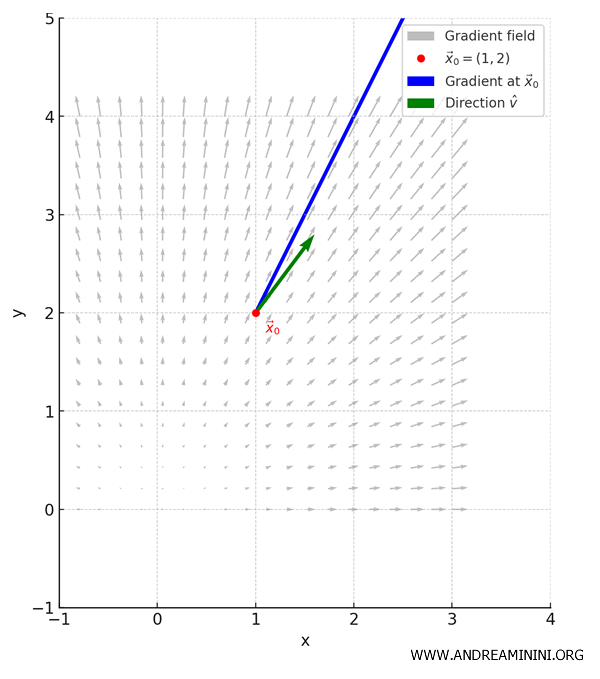
Volendo dare un'occhiata alla funzione in 3D, la superficie della funzione \( f(x, y) = x^2 + y^2 \) si presenta come una cupola rovesciata o una ciotola.

Il punto rosso \( \vec{x}_0 = (1, 2) \) è quello preso in esame.

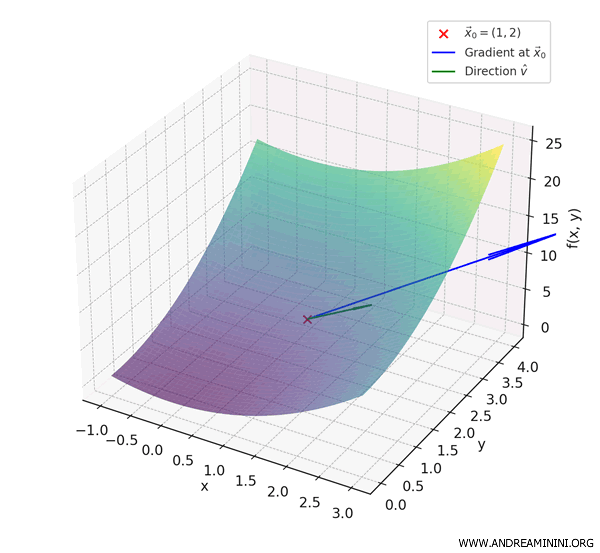
Il vettore blu è il gradiente, che parte da \( \vec{x}_0 \) e punta dritto nella direzione di massima salita.

Il vettore verde è la direzione \( \hat{v} \) e indica quanto sale la funzione in questa direzione.

Dimostrazione

Devo dimostrare che, se \( f \) è differenziabile in \( \vec{x}_0 \), allora la formula della derivata direzionale nel punto \( \vec{x}_0 \) lungo una direzione \( \vec{v} \) è il prodotto scalare \( \cdot \) del gradiente \( \vec{\alpha} \) (o derivata lineare) di \( f \) in \( \vec{x}_0 \) e del vettore direzione \( \vec{v} \)

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\alpha} \cdot \vec{v} \]

Considero come ipotesi iniziale una \( f \) differenziabile in \( \vec{x}_0 \). Per definizione, ciò significa che:

\[ f(\vec{x}_0 + \vec{h}) = f(\vec{x}_0) + \vec{\alpha} \cdot \vec{h} + o(|\vec{h}|) \quad \text{per } \vec{h} \to 0 \]

Questo è lo sviluppo di Taylor al primo ordine senza resto esplicito, dove \( \vec{\alpha} \) è il vettore che rappresenta la derivata (o gradiente) di \( f \) in \( \vec{x}_0 \) e \( o(|\vec{h}|) \) rappresenta un errore infinitesimo di ordine superiore (più piccolo di \( |\vec{h}| \)).

Prendo una direzione \( \vec{v} \) generica.

La derivata di \( f \) in \( \vec{x}_0 \) nella direzione \( \vec{v} \) è definita come:

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) := \lim_{t \to 0} \frac{f(\vec{x}_0 + t\vec{v}) - f(\vec{x}_0)}{t} \]

A questo punto uso la formula della differenziabilità, ponendo \( \vec{h} = t\vec{v} \).

\[ f(\vec{x}_0 + \vec{h}) = f(\vec{x}_0) + \vec{\alpha} \cdot \vec{h} + o(\|\vec{h}\|) \quad \text{per } \vec{h} \to \vec{0} \]

\[ f(\vec{x}_0 + t\vec{v}) = f(\vec{x}_0) + \vec{\alpha} \cdot (t\vec{v}) + o(|t\vec{v}|) \]

Sostituisco \( f(\vec{x}_0 + t\vec{v}) \) nella definizione della derivata direzionale:

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \lim_{t \to 0} \frac{f(\vec{x}_0 + t\vec{v}) - f(\vec{x}_0)}{t} \]

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0)  = \lim_{t \to 0} \frac{f(\vec{x}_0) + \vec{\alpha} \cdot (t\vec{v}) + o(|t\vec{v}|) - f(\vec{x}_0)}{t} \]

Cancello \( f(\vec{x}_0) \) con \( -f(\vec{x}_0) \):

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0)  = \lim_{t \to 0} \frac{t (\vec{\alpha} \cdot \vec{v}) + o(t|\vec{v}|)}{t} \]

In questo caso ho utilizzato \( \vec{\alpha} \cdot (t\vec{v}) = t (\vec{\alpha} \cdot \vec{v}) \) e \( |t\vec{v}| = |t||\vec{v}| = t|\vec{v}| \) per \( t \to 0 \) che può essere positivo o negativo.

Separo i due termini del numeratore:

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0)   = \lim_{t \to 0} \left[ \frac{ t  \vec{\alpha} \cdot \vec{v} }{t} + \frac{o(t|\vec{v}|)}{t} \right] \]

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0)   = \lim_{t \to 0} \left[ \vec{\alpha} \cdot \vec{v} + \frac{o(t|\vec{v}|)}{t} \right] \]

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0)   = \lim_{t \to 0} \vec{\alpha} \cdot \vec{v} + \lim_{t \to 0} \frac{o(t|\vec{v}|)}{t}  \]

Poiché \( \frac{o(t|\vec{v}|)}{t|\vec{v}|} \to 0 \) per definizione di simbolo “\( o \)”, allora tutto il secondo lmite va a 0.

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0)   = \lim_{t \to 0} \vec{\alpha} \cdot \vec{v} \]

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\alpha} \cdot \vec{v} \]

Ho dimostrato che la derivata direzionale è il prodotto scalare del gradiente \( \vec{\alpha} \) con la direzione \( \vec{v} \).

Altri esempi

Considero la funzione di due variabili \( f(x, y) = x^2 - xy \) e voglio calcolare la derivata direzionale di \( f \) nel punto \( (-1, 2) \) nella direzione del vettore \( \mathbf{v} = (-1, 3) \).

Per prima cosa calcolo il gradiente \( \nabla f(x, y) \) della funzione che è dato dal vettore delle derivate parziali:

\[ \nabla f(x, y) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) \]

Le derivate parziali della funzione sono:

• \( \frac{\partial f}{\partial x} = 2x - y \)
• \( \frac{\partial f}{\partial y} = -x \)

Quindi, il gradiente della funzione è:

\[ \nabla f(x, y) = (2x - y, -x) \]

A questo punto valuto il valore del gradiente nel punto \( (-1, 2) \) sostituendo \( x = -1 \) e \( y = 2 \) nel gradiente:

\[ \nabla f(-1, 2) = (2(-1) - 2, -(-1)) = (-2 - 2, 1) = (-4, 1) \]

Per ottenere la derivata direzionale, calcolo il prodotto scalare tra il gradiente (-4,1) e il vettore direzione (-1,3):

\[ D_{\mathbf{v}}f(-1, 2) = \nabla f(-1, 2) \cdot \mathbf{v} = (-4, 1) \cdot (-1, 3) \]

\[ D_{\mathbf{v}}f(-1, 2) = (-4)(-1) + (1)(3) = 4 + 3 = 7 \]

Il valore trovato, 7, rappresenta la derivata direzionale della funzione \( f \) nel punto \( (-1, 2) \) lungo la direzione del vettore \( \mathbf{v} = (-1, 3) \).

Significa che se mi trovo sul grafico della funzione nel punto \( (-1, 2, f(-1,2)) = (-1, 2, 3) \) e mi muovo nella direzione \( \mathbf{v} \), la funzione aumenta con un tasso di crescita pari a 7 ovvero mi sposto in salita.

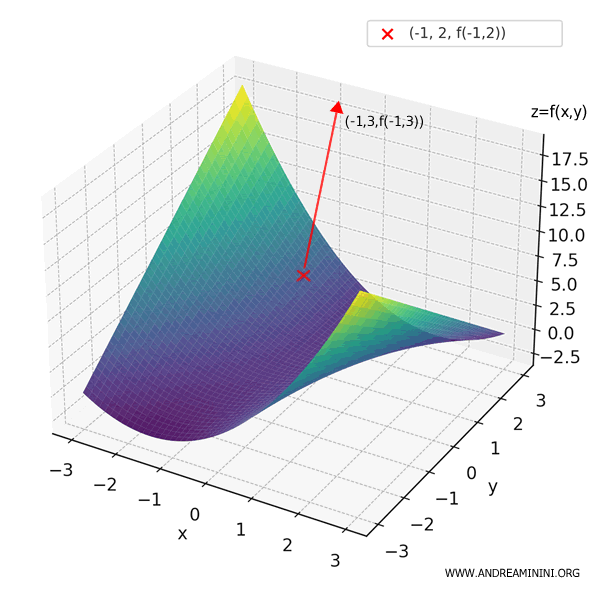
Per ottenere un valore normalizzato basta dividere il prodotto scalare per la lunghezza del vettore direzione (-1,3) ossia per la sua norma.

\[ D_{\mathbf{v}}f(-1, 2) = \nabla f(-1, 2) \cdot \frac{ \mathbf{v} }{ || \mathbf{v} ||} = \frac{ (-4, 1) \cdot (-1, 3) }{ \sqrt{1^2+3^2}  } \]

\[ D_{\mathbf{v}}f(-1, 2) = \frac{ (-4)(-1) + (1)(3) }{ \sqrt{1+9}  } = \frac{ 7 }{ \sqrt{10}  } \approx 2.21 \]

Nota: la direzione in cui la funzione cresce più rapidamente è quella del gradiente stesso, cioè il vettore \( (-4, 1) \). Quindi, per salire al massimo, dovrei muovermi nella direzione \( (-4, 1) \). \[ D_{\mathbf{v}}f(-1, 2) = \nabla f(-1, 2) \cdot \frac{ \nabla f(-1, 2) }{ || \nabla f(-1, 2) ||} = \frac{ (-4, 1) \cdot (-4, 1) }{ \sqrt{(-4^2+1^2} } \] \[ D_{\mathbf{v}}f(-1, 2) = \frac{ -4 \cdot (-4) + 1 \cdot 1 }{ \sqrt{16+1} } = \frac{17}{\sqrt{17}} = \sqrt{17} \approx 4.12 \]

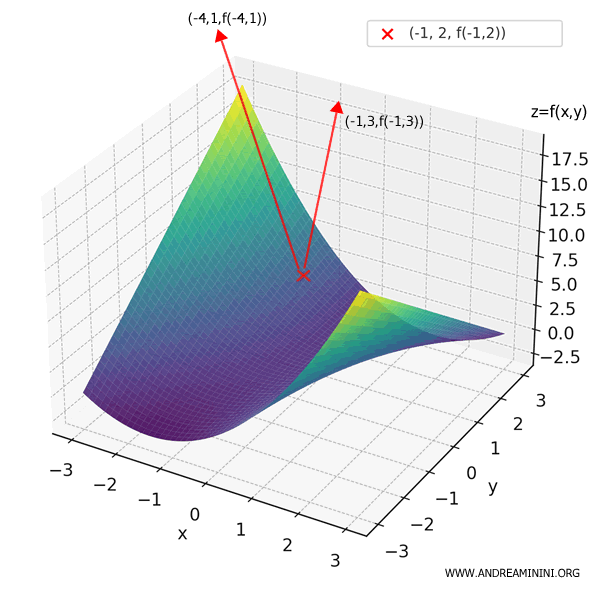
Cosa succede se mi muovo nella direzione \( \mathbf{w} = (1, 3) \) invece di \( \mathbf{v} = (-1, 3) \)?

Il gradiente calcolato prima è ancora valido:

\[ \nabla f(-1, 2) = (-4, 1) \]

Quindi, mi basta calcolare il prodotto scalare tra il gradiente e la nuova direzione \( \mathbf{w} = (1,3) \):

\[ D_{\mathbf{w}}f(-1, 2) = (-4, 1) \cdot (1, 3) = (-4)(1) + (1)(3) = -4 + 3 = -1 \]

La derivata direzionale è negativa, cioè \( D_{\mathbf{w}}f(-1, 2) = -1 \). Questo significa che se mi sposto dal punto \((-1, 2)\) lungo la direzione \( (1, 3) \), la funzione decresce.

In altre parole, se mi sposto lungo la direzione \( (1, 3) \), sto scendendo sul grafico della funzione.

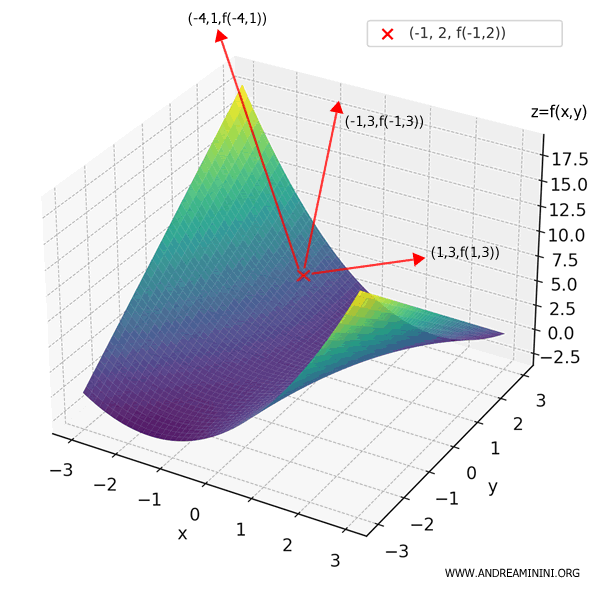
Per concludere calcolo anche il valore normalizzato in questa direzione.

\[ D_{\mathbf{v}}f(-1, 2) = \nabla f(-1, 2) \cdot \frac{ \mathbf{v} }{ || \sqrt{ \mathbf{v} } ||}  = \frac{ (-4, 1) \cdot (1, 3) }{ \sqrt{1^2+3^2}  } \]

\[ D_{\mathbf{v}}f(-1, 2) = \frac{ (-4)(1) + (1)(3) }{ \sqrt{1+9} } = \frac{ -4 + 3 }{ \sqrt{10} } = \frac{ -1 }{ \sqrt{10} } \approx -0.316   ]

In questo modo posso confrontare tra loro i valori normalizzati che ho appena calcolato.

Note

Alcune osservazioni e note aggiuntive.

• Il legame tra le derivate direzionali e le derivate parziali

  La derivata parziale di \( f \) rispetto a \( x_k \) nel punto \( \vec{x}_0 \) è la k-esima componente del gradiente di \( f \) in quel punto.

  In altre parole, le derivate parziali sono casi particolari di derivate direzionali, in cui il vettore direzione \( \vec{v} \) è uno dei vettori della base canonica, cioè \( \vec{e}_k \). Dove \( \vec{e}_k \) è il vettore unitario con 1 nella k-esima posizione e 0 altrove. Ad esempio, in \( \mathbb{R}^3 \): \[ \vec{e}_1 = (1, 0, 0), \quad \vec{e}_2 = (0, 1, 0), \quad \vec{e}_3 = (0, 0, 1) \] Come si collega alle derivate parziali? La derivata parziale rispetto a \( x_k \) si può scrivere come derivata direzionale nella direzione \( \vec{e}_k \): \[ \frac{\partial f}{\partial x_k}(\vec{x}_0) = \frac{\partial f}{\partial \vec{e}_k}(\vec{x}_0) \] Ma dalla formula della derivata direzionale ottengo: \[ \frac{\partial f}{\partial \vec{e}_k}(\vec{x}_0) = \vec{\alpha} \cdot \vec{e}_k \] Dove \( \vec{\alpha} = \nabla f(x_0) \) è il gradiente.  E ora il punto chiave, il prodotto scalare con \( \vec{e}_k \) seleziona la k-esima componente del gradiente \( \vec{\alpha} \). \[ \frac{\partial f}{\partial \vec{e}_k}(\vec{x}_0) = \vec{\alpha} \cdot \vec{e}_k = \alpha_k \] Quindi, la derivata parziale di \( f \) rispetto a \( x_k \) nel punto \( \vec{x}_0 \) è la k-esima componente del gradiente di \( f \) in quel punto. Data una derivata parziale \( \frac{\partial f}{\partial x_k} \) e una dervata direzionale in una direzione qualsiasi \( \frac{\partial f}{\partial \vec{v}} \), se \( \vec{v} = \vec{e}_k \) la direzionale coincide con la parziale.

  Esempio. Considero la funzione \[ f(x, y) = 3x^2y + 2y \] Le derivate parziali della funzione sono \[ \frac{\partial f}{\partial x} = 6xy, \quad \frac{\partial f}{\partial y} = 3x^2 + 2 \] Quindi, il gradiente della funzione è \[ \nabla f(x, y) = \left( 6xy,\ 3x^2 + 2 \right) \] Nel punto \( (1, 2) \) il gradiente è: \[ \nabla f(1, 2) = (6 \cdot 1 \cdot 2,\ 3 \cdot 1^2 + 2) = (12,\ 5) \] La derivata parziale rispetto a \( x \) in \( (1, 2) \) è \[ \frac{\partial f}{\partial x}(1, 2) = 6 \cdot 1 \cdot 2 = 12 \] Ora, la derivata direzionale lungo \( \vec{e}_1 = (1, 0) \) si calcola usando la formula:\[ \frac{\partial f}{\partial \vec{e}_1}(1, 2) = \nabla f(1, 2) \cdot \vec{e}_1 = (12,\ 5) \cdot (1,\ 0) = 12 \] Questo conferma che la derivata parziale è la derivata direzionale lungo il vettore della base canonica \( \vec{e}_1 \). \[ \frac{\partial f}{\partial x}(1, 2) = 12 \quad \text{e} \quad \nabla f(1, 2) \cdot \vec{e}_1 = 12 \] Questa è la visualizzazione del campo vettoriale con i vettori normalizzati.
  

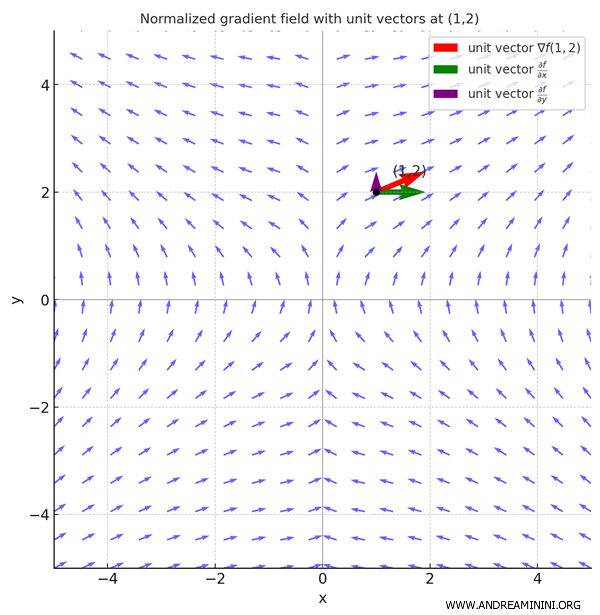
• Il gradiente è un vettore orientato nella direzione di massima crescita

  Il gradiente \( \nabla f(x_0) \) è un vettore che punta nella direzione di massima crescita della funzione.

  La lunghezza del gradiente indica quanto velocemente la funzione cresce in quella direzione.

  Dimostrazione. Parto dalla formula della derivata direzionale di \( f \) nel punto \( x_0 \) lungo una direzione \( \vec{v} \) che è uguale al prodotto scalare tra il gradiente di \( f \) in quel punto e il vettore direzione \( \vec{v} \). \[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\nabla}f(x_0) \cdot \vec{v} \] Essendo un prodotto scalare tra due vettori posso scriverlo come il prodotto tra i moduli dei due vettori per il coseno dell'angolo \( \theta \) compreso tra questi \[ \frac{\partial f}{\partial \vec{v}}(x_0) = |\nabla f(x_0)| \cdot |\vec{v}| \cdot \cos\theta \] Questa formula dice che la derivata direzionale in una direzione \( \vec{v} \) è proporzionale alla lunghezza del gradiente \( |\nabla f(x_0)| \) e alla lunghezza del vettore direzione \( |\vec{v}| \) (che di solito si prende unitario, cioè con \( |\vec{v}| = 1 \)), e soprattutto dipende dall’angolo \( \theta \) tra il gradiente \( \nabla f \) e la direzione \( \vec{v} \), tramite il coseno. La chiave è capire come varia il coseno dell’angolo.

  • Quando \( \cos \theta = 1 \), cioè \( \theta = 0^\circ \), i due vettori sono allineati. Quindi, la derivata direzionale è massima nella stessa direzione del gradiente.
  • Quando \( \cos \theta = -1 \), cioè \( \theta = 180^\circ \), i vettori sono opposti. Quindi, la derivata direzionale è minima nella direzione opposta al gradiente.
  • Quando \( \cos \theta = 0 \), cioè \( \theta = 90^\circ \), i vettori sono ortogonali. Pertanto, la derivata direzionale è zero e la funzione non cambia in quella direzione.

  Questo dimostra che il gradiente \( \nabla f(x_0) \) è un vettore che punta nella direzione di massima crescita della funzione e la sua lunghezza indica quanto velocemente la funzione cresce in quella direzione.

E così via.