La rappresentazione di una funzione di due variabili
Per disegnare nello spazio una funzione di due variabili f(x,y)
$$ z=f(x,y)=x^2 + y^2 $$
pongo a zero la variabile y=0 e calcolo il valore della funzione al variare di x.
$$ z=f(x,0) = x^2 $$
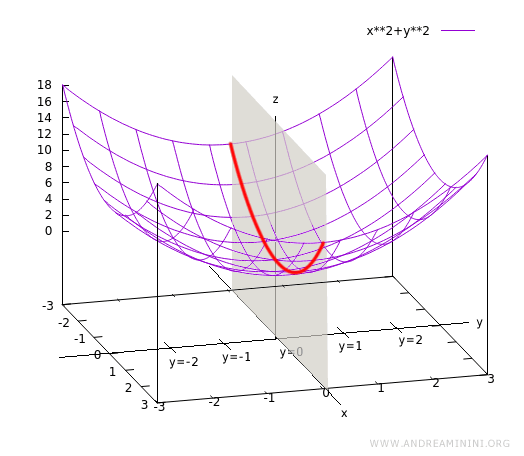
Ottengo un grafico sul piano xz
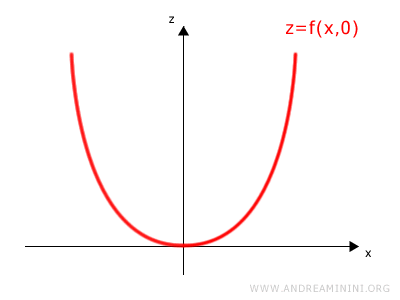
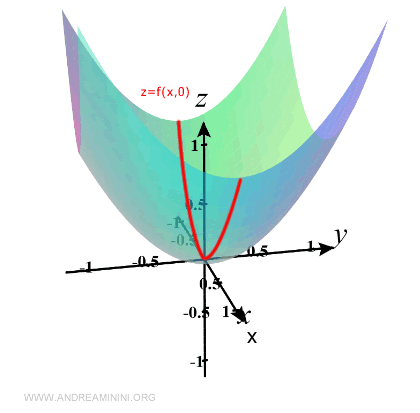
Questa curva si presenta nella funzione z=f(x,y) quando la variabile y è nulla.
In pratica è la curva che si trova sul piano xz quando y=0.
Adesso pongo a zero la variabile x=0 e calcolo il valore della funzione al variare di y.
$$ z=f(0,y) = y^2 $$
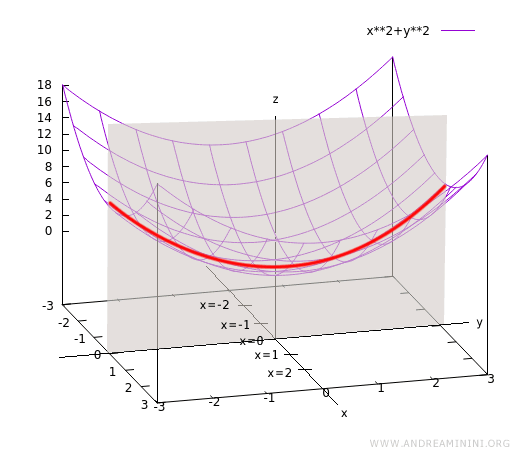
Ottengo un grafico sul piano yz
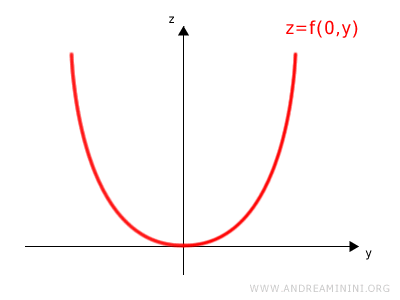
Questa curva si presenta nella funzione z=f(x,y) quando la variabile x è nulla.
In pratica è la curva che si trova sul piano yz quando x=0.
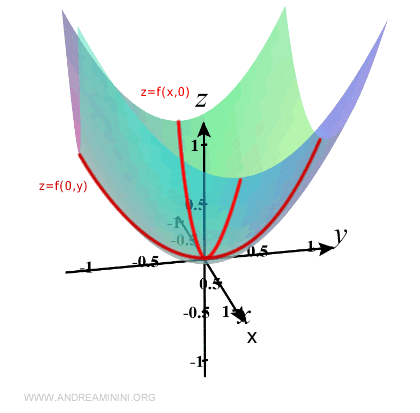
Ora ripeto la stessa operazione per valori x e y diversi.
Quello che ottengo è un grafico locale della funzione di due variabili.
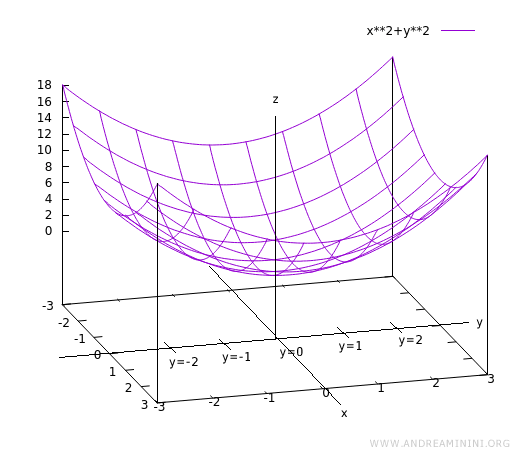
Nota. Quando calcolo un nuovo il valore della funzione al variare di x con y costante, ad esempio f(x,y=1), ottengo un'altra curva sul piano xz. Le curve sul piano xz però non si sovrappongono perché appartengono a un valore y diverso. Il piano xz interseca l'asse delle y in modo ortogonale a un valore diverso (es. y=1). Lo stesso discorso vale per altri valori y=2, y=3, ...
Oltre al piano xz c'è anche il piano yz che mostra i valori z al variare di y mantenendo x=0. I piano yz paralleli intersecano l'asse x a diversi valori x=1, x=2, ecc. Pertanto, ci sono due famiglie di piani xz e yz da considerare.
Posso riscrivere le equazioni del grafico sui piani xz e yz anche da un punto di vista parametrico
Asse x:
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} +t \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} $$
Asse y:
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} +t \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$
Ad esempio, per disegnare il grafico sul piano xz che interseca l'asse y mantenendo costante il valore y=1 l'equazione parametrica è
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} +t \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} $$
Pertanto, se la funzione è
$$ z=x^2+y^2 $$
La funzione diventa
$$ z=x^2+1 $$
E così via.
