Il minimo e il massimo di una funzione di due variabili con le linee di livello
Il metodo delle linee di livello è una tecnica grafica per trovare il massimo o il minimo di una funzione $f(x, y)$ su un insieme $A$, cioè sul dominio della funzione.
È un metodo intuitivo e visivo, particolarmente utile per funzioni semplici e per domini delimitati (ad esempio poligoni).
Cosa sono le linee di livello?
Le linee di livello sono le curve nel piano $(x, y)$ lungo le quali la funzione $f(x, y)$ assume un valore costante:
$f(x, y) = \lambda$
In pratica, ogni linea di livello rappresenta tutti i punti del piano in cui la funzione ha lo stesso valore $\lambda$.
Come funziona il metodo?
Il procedimento è semplice e si basa su un ragionamento geometrico:
- Disegno il dominio $A$
- Rappresento l'insieme $A$ sul piano $(x,y)$. Questo insieme delimita l'area in cui cerco il massimo e il minimo della funzione.
- Disegno le linee di livello di $f(x, y)$
- Traccio varie curve $f(x, y) = \lambda$ per diversi valori di $\lambda$. Ogni curva indica dove la funzione vale $\lambda$.
- Individuo il massimo e il minimo
Il massimo è associato alla linea di livello più alta (cioè con $\lambda$ maggiore) che interseca o tocca $A$.
Il minimo è la linea di livello più bassa (cioè con $\lambda$ minore) che tocca $A$.
Quando è utile? Il metodo è molto efficace quando le funzioni sono semplici o con simmetrie (quadrati, cerchi, ellissi), domini *poligonali o delimitati. In altre parole, nelle situazioni in cui è possibile capire visivamente il comportamento della funzione. Per funzioni più complesse o domini irregolari, il metodo resta utile per un primo approccio qualitativo prima di passare a tecniche analitiche più rigorose.
Esempio
Considero la funzione:
$f(x, y) = x^2 + y^2$
e il dominio $A$: un quadrato definito da $-1 \leq x \leq 1$, $-1 \leq y \leq 1$.
Disegno il quadrato $A$ nel piano $(x, y)$.
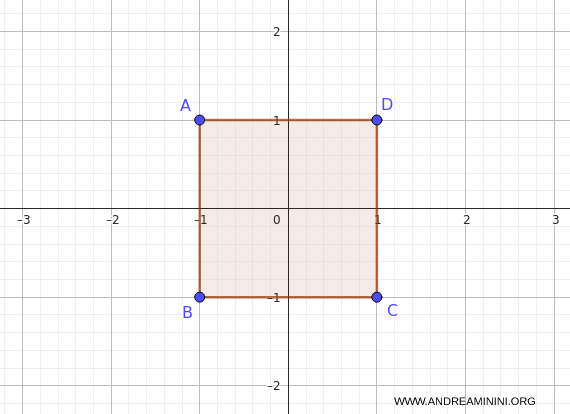
Le linee di livello sono circonferenze con raggio $\sqrt{\lambda}$ centrate nell'origine.
$$ x^{2}+y^{2}=\lambda,\qquad \lambda\ge 0. $$
Se risolvo per $y$ ottengo
$$ y^{2}=\lambda-x^{2}\quad\Longrightarrow\quad y=\pm\sqrt{\lambda-x^{2}} $$
Perché la curva di livello intersechi il vincolo dev’essere
Poi disegno le curve di livello variando $ \lambda $.
In questo caso $ \lambda \ge 0 $ deve essere non negativo.
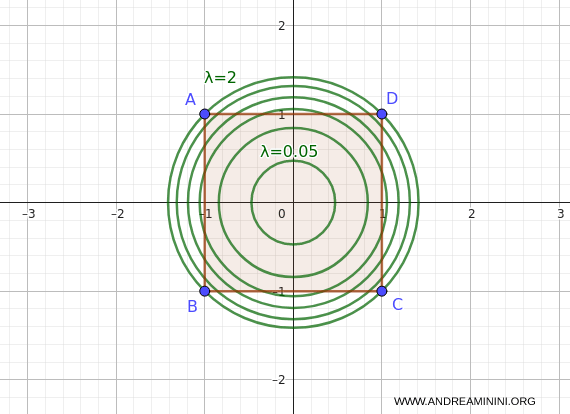
La circonferenza più piccola che interseca $A$ è il cerchio di raggio 0: il punto $(0,0)$, dove $f(0,0) = 0$.
Quindi, il minimo assoluto della funzione nel dominio è $0$ nel punto $ (x,y)=(0,0) $.
La circonferenza più grande che ancora tocca il dominio è quella che passa per i vertici del quadrato.
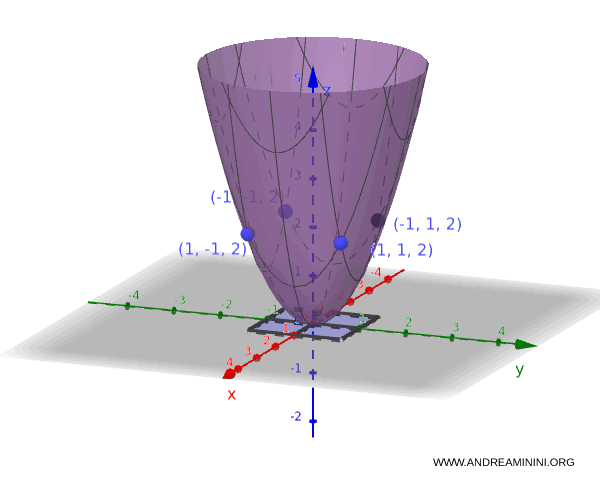
$$f(1,1) = 1^2 + 1^2 = 2$$
Quindi, il massimo assoluto della funzione nel dominio è $2$ nei punti $(1,1)$, $(-1,1)$, $ (1,-1) $ e $ (-1,-1) $.
Con un semplice disegno ho trovato che il minimo e il massimo della funzione.
Esempio 2
Ho la funzione
$$ f(x,y) = x-2y $$
nel vincolo
$$ x^2+y^2 \le 3 $$
Devo trovare il minimo e il massimo della funzione entro il vincolo, usando il metodo delle linee di livello.
Per prima cosa disegno il vincolo che, in questo caso, è un cerchio $ x^2+y^2 \le 3 $.
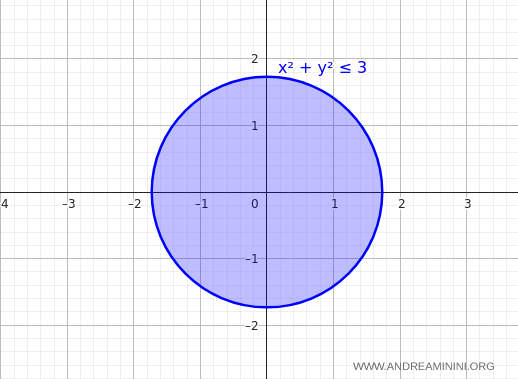
La funzione può avere diversi valori sull'asse z che indico con $ \lambda $
$$ f(x,y) = x-2y = \lambda $$
Ricavo $ y $ in funzione di $ x $ e $ \lambda $
$$ x - \lambda = 2y $$
$$ y = \frac{x - \lambda}{2} $$
Ora disegno le linee di livello assegnando vari valori a $ \lambda $
Le linee di livello con il valore più alto sono quelle in basso, mentre quelle con il valore più basso sono quelle in alto.

Quindi, il valore massimo della funzione $ f(x,y) $ è la retta tangente alla circonferenza (bordo del vincolo) in basso.
Il valore minimo della funzione $ f(x,y) $, invece, è la retta tangente alla circonferenza in alto.
Quali sono i valori $ \lambda $ del minimo e del massimo?
Dunque ho trovato l'equazione delle linee di livello
$$ y = \frac{x - \lambda}{2} $$
Sostituisco la variabile $ x $ nell'equazione che rappresenta il bordo del vincolo
$$ x^2 + \left( \frac{x - \lambda}{2} \right)^2 = 3 $$
$$ x^2 + \frac{(x - \lambda)^2}{4} = 3$$
Moltiplico tutto per 4 così mi libero dei denominatori:
$$ 4x^2 + (x - \lambda)^2 = 12 $$
Espando il quadrato:
$$ 4x^2 + x^2 - 2x\lambda + \lambda^2 = 12 $$
$$ 5x^2 - 2x\lambda + \lambda^2 = 12 $$
Il risultato è una equazione quadratica in $x$.
Quindi mi calcolo il discriminante:
$$ \Delta = [-2\lambda]^2 - 4 \cdot 5 \cdot (\lambda^2 - 12)$$
$$ \Delta = 4\lambda^2 - 20(\lambda^2 - 12) $$
$$ \Delta = 4\lambda^2 - 20\lambda^2 + 240 $$
$$ \Delta = -16\lambda^2 + 240 $$
Per essere una retta tangente è necessario che ci sia un'unico punto in comune, ossia che il discriminante sia nullo $ \Delta = 0 $.
$$ \Delta = -16\lambda^2 + 240 = 0 $$
$$ -16\lambda^2 + 240 = 0 $$
$$ 16\lambda^2 = 240 $$
$$ \lambda^2 = \frac{240}{16}$$
$$ \lambda^2 = 15 $$
$$ \lambda = \pm \sqrt{15} $$
Quindi il valore massimo e minimo della funzione $f(x, y)$ soggetta al vincolo sono:
$$ \lambda_{max} = \sqrt{15} \approx 3.873 $$
$$ \lambda_{min} = -\sqrt{15} \approx -3.873 $$
E così via.
