Trasformazioni involutorie in geometria
Una trasformazione involutoria in geometria è una trasformazione geometrica che, se applicata due volte, lascia l'oggetto invariato, ovvero porta all'identità.
In altre parole, si tratta di una trasformazione \( T \) che, quando è applicata due volte consecutivamente ad un oggetto geometrico (es. figura piana, solido, ecc.), restituisce l'oggetto originale come risultato finale.
Dal punto di vista matematico, posso scrivere una trasformazione involutoria come una funzione composta che applico a ogni punto \( x \) di un oggetto e restituisce il punto stesso.
$$ T(T(x)) = x $$
Le trasformazioni involutorie si trovano in diverse aree della geometria, come la geometria euclidea, la geometria proiettiva e la geometria algebrica. Hanno diverse proprietà interessanti.
Ecco alcuni esempi pratici di trasformazioni geometriche involutorie:
- Riflessione (simmetria assiale)
La riflessione rispetto a una retta (nel piano) o a un piano (nello spazio) è un esempio comune di trasformazione involutoria. Se applico due volte la riflessione rispetto alla stessa retta o piano, ogni punto dell'oggetto torna alla sua posizione originale.
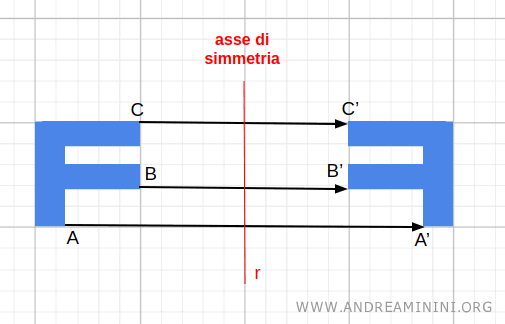
- Simmetria centrale
La simmetria rispetto a un punto è un'altra trasformazione involutoria. Se applico due volte la stessa simmetria centrale a un punto, questo torna nella posizione iniziale.
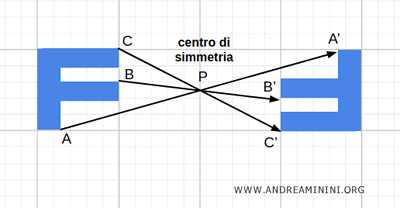
La trasformazione involutoria nella geometria analitica
Una trasformazione $ t $ si dice involutoria se coincide con la propria inversa $ t^{-1} $. $$ t = t^{-1} $$
In altre parole, applicandola due volte di seguito, ottengo la trasformazione identica, che lascia invariati tutti i punti.
$$t \circ t = i $$
Dove $i$ è la trasformazione identica.
Questo implica che la trasformazione coincide con la sua inversa $t \circ t = i \Leftrightarrow t = t^{-1} $.
Esempio
Considero la trasformazione $ t $ definita dalle equazioni:
$$ t: \begin{cases} x' = -x \\ \\ y' = -y \end{cases} $$
Questa trasformazione associa a ogni punto $P(x, y)$ il punto $P'(-x, -y)$.
Applicandola due volte ottengo
- $P(x, y) \mapsto P'(-x, -y)$
- $P'(-x, -y) \mapsto P''(x, y) = P$
Quindi, $ t \circ t = i$, la trasformazione $ t $ è involutoria perché riporta al punto di partenza $ P $.
Ad esempio, se applico la trasformazione $ t $ sul punto $ P(1,2) $ ottengo:
- $P(1, 2) \mapsto P'(-1, -2)$
- $P'(-1, -2) \mapsto P''(1, 2)$
Il punto finale $ P'' $ coincide con il punto iniziale $ P(1,2) $.
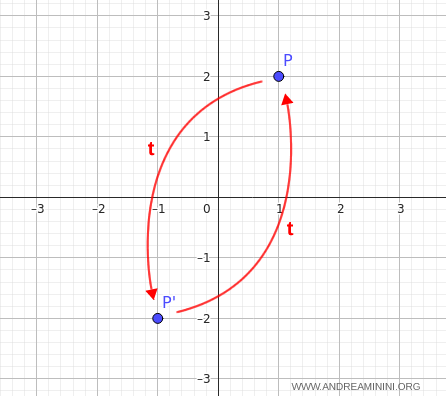
Pertanto, applicarla due volte equivale a non aver fatto nulla.
E così via.
