La rotazione

La rotazione è una trasformazione geometrica che avviene nel piano, in cui ogni punto di una figura viene spostato attorno a un punto fisso, noto come centro di rotazione.

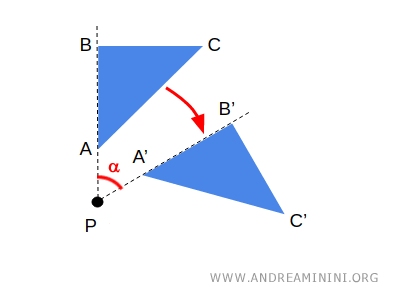
Sul piano una rotazione r(P;α) di centro P e angolo α, a ogni punto A fa corrispondere un punto A', tale che il segmento PA è congruente con il segmento PA' e l'angolo APA' ha lo stesso orientamento ed è congruente con l'angolo della rotazione α.

 

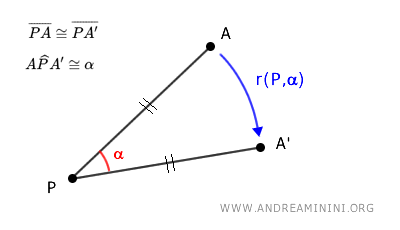
In altre parole, la rotazione è una trasformazione che sposta i punti (A) di una figura attorno a un centro di rotazione (P), senza alterare la forma o le dimensioni della figura stessa.

La figura risultante dalla rotazione è congruente con la figura originale, il che significa che hanno la stessa forma e dimensione. Pertanto, la rotazione è classificata come una isometria, poiché conserva le distanze tra i punti.

Le caratteristiche della rotazione

Ogni rotazione è caratterizzata dai seguenti elementi

• il centro di rotazione
• l'ampiezza dell'angolo di rotazione
• il verso della rotazione.

Il centro di rotazione è il punto P attorno al quale avviene la rotazione della figura.

 

Durante questa trasformazione, ogni punto della figura ruota di un angolo definito, α, mantenendo inalterata la sua distanza dal centro di rotazione.

$$ \overline{PA} \cong \overline{PA'} $$

$$ \overline{PB} \cong \overline{PB'} $$

Quindi, il centro è l'unico punto unito della rotazione.

L'angolo corrispondente all'arco tracciato dai punti è congruente con l'angolo di rotazione α.

$$ APA' \cong \alpha $$

$$ BPB' \cong \alpha $$

L'angolo di rotazione è l'angolo α che determina di quanto un punto della figura viene ruotato attorno al centro di rotazione.

Si tratta di un angolo orientato, quindi è molto importante indicare anche il verso della rotazione.

Il verso della rotazione può essere sia in senso orario che antiorario.

• Antiorario
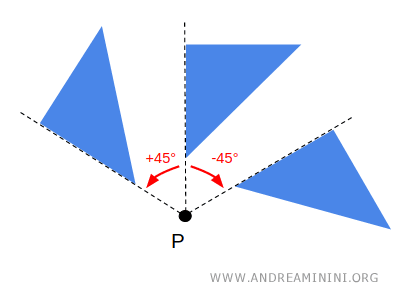
  La rotazione nel verso antiorario è tradizionalmente rappresentata da un angolo con segno positivo (ad esempio, +45°).
• Orario
  La rotazione nel verso orario è rappresentata da un angolo con segno negativo (ad esempio, -45°).

Le equazioni della rotazione

La rotazione di un punto P(x,y) rispetto all'origine O degli assi si realizza usando questo sistema di equazioni: $$ \begin{cases} x' = x \cdot \cos \alpha - y \cdot \sin \alpha \\ \\ y'= x \cdot \sin \alpha + y \cdot \cos \alpha \end{cases} $$

Le formule di rotazione forniscono le coordinate P'(x′,y′) di un punto P(x;y) dopo che è stato ruotato attorno all'origine (0,0) di un certo angolo α.

Le formule sono particolarmente semplici quando la rotazione avviene di un angolo retto, cioè di α=90°.

• La rotazione di un angolo retto in senso orario
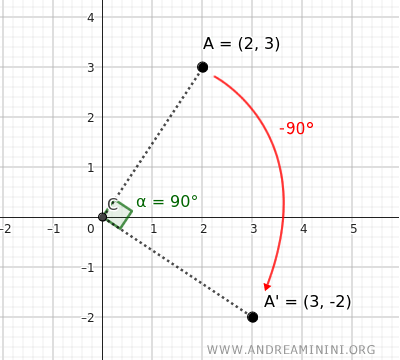
  Quando ruoto un punto P(x;y) di 90° in senso orario attorno all'origine O(0;0), il risultato è un punto P'(x';y') in cui la nuova coordinata x′ corrisponde alla vecchia coordinata y, mentre la nuova coordinata y′ è l'opposto della vecchia coordinata x. $$ \begin{cases} x' = y \\ \\ y'=-x \end{cases} $$

  Esempio. Devo ruotare il punto A=(2;3) di 90° in senso orario (-90°). Applico la formula precedente e ottengo il punto A'=(3;-2).
  

• La rotazione di un angolo retto in senso antiorario
  In questo caso la rotazione di 90° in senso antiorario di un punto P(x;y) attorno all'origine degli assi O(0;0) genera un nuovo punto P'(x';y') in cui la nuova coordinata x′ è l'opposto della vecchia coordinata y, mentre la nuova coordinata y′ corrisponde alla vecchia coordinata x. $$ \begin{cases} x' = -y \\ \\ y'=x \end{cases} $$

  Esempio. Per ruotare il punto A=(2;3) di 90° in senso antiorario (+90°), utilizzo la formula di rotazione precedente. Dopo aver applicato la formula, determino le nuove coordinate del punto come A'=(-3;2).
  

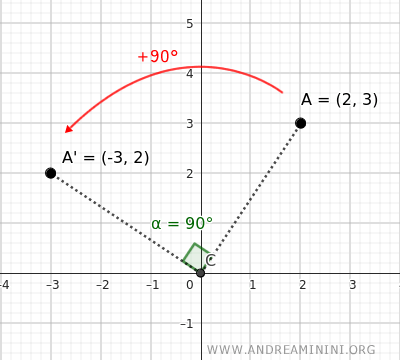
In entrambi i casi, si può notare come le coordinate originali vengano "scambiate" tra loro, con l'aggiunta di un segno negativo a seconda della direzione della rotazione.

In generale, la rotazione di un angolo α intorno all'origine degli assi si può ottenere usando questa formula

$$ \begin{cases} x' = x \cdot \cos \alpha - y \cdot \sin \alpha \\ \\ y'= x \cdot \sin \alpha + y \cdot \cos \alpha \end{cases} $$

Lo stesso sistema di equazioni posso rappresentarlo in forma vettoriale nel seguente modo

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos \alpha & - \sin \alpha \\ \sin \alpha & \cos \alpha \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} $$

Dove la matrice con le formule trigonometriche (seno e coseno) è detta matrice di rotazione.

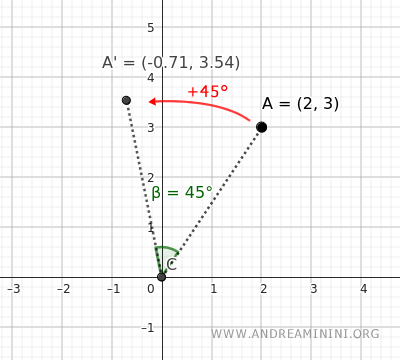
Esempio. Voglio far ruotare il punto A=(2;3) di 45° in senso antiorario (+45°). Quindi, utilizzo la formula di rotazione precedente. $$ \begin{cases} x' = x \cdot \cos \alpha - y \cdot \sin \alpha \\ \\ y'= x \cdot \sin \alpha + y \cdot \cos \alpha \end{cases} $$ Sostituisco le coordinate del punto A che voglio far ruotare, ossia x=2 e y=3 $$ \begin{cases} x' = 2 \cdot \cos \alpha - 3 \cdot \sin \alpha \\ \\ y'= 2 \cdot \sin \alpha + 3 \cdot \cos \alpha \end{cases} $$ Utilizzo l'angolo di rotazione α=45° con segno positivo perché il verso della rotazione è in senso antiorario. $$ \begin{cases} x' = 2 \cdot \cos 45° - 3 \cdot \sin 45° \\ \\ y'= 2 \cdot \sin 45° + 3 \cdot \cos 45° \end{cases} $$ Calcolo il valore del seno e del coseno di 45° che approssimativamente sono sin(45°)=0,71 e cos(45°)=0,71 e li sostituisco nella formula. $$ \begin{cases} x' = 2 \cdot 0,71 - 3 \cdot 0,71 \\ \\ y'= 2 \cdot 0,71 + 3 \cdot 0,71 \end{cases} $$ $$ \begin{cases} x' = 1,42 - 2.13 \\ \\ y'= 1,42 + 2,13 \end{cases} $$ $$ \begin{cases} x' = - 0,71 \\ \\ y'= 3,54 \end{cases} $$ Le coordinate del punto A' dopo la rotazione di 45° sono (x';y')=(-0,71;3,54).

Casi particolari della rotazione

In alcuni casi notevoli, le formule della rotazione si semplificano in modo significativo:

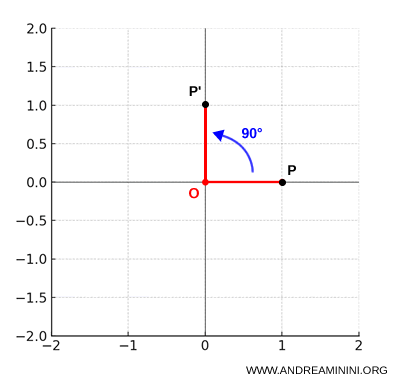
• Rotazione di 90° in senso antiorario: se l’angolo è $\alpha = \frac{\pi}{2}$ radianti, allora $\cos \alpha = 0$ e $\sin \alpha = 1$. Le equazioni della rotazione diventano: $$ \begin{cases} x' = -y \\ y' = x \end{cases} $$

  

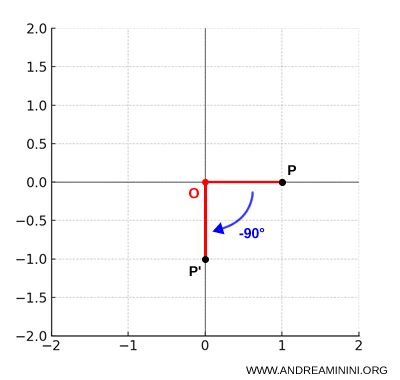
• Rotazione di 90° in senso orario: se l’angolo è $\alpha = -\frac{\pi}{2}$, allora $\cos \alpha = 0$ e $\sin \alpha = -1$. Le equazioni si riducono a: $$ \begin{cases} x' = y \\ y' = -x \end{cases} $$

  

• Rotazione nulla o rotazione completa: se $\alpha = 0$ oppure $\alpha = 2\pi$, allora $\cos \alpha = 1$ e $\sin \alpha = 0$, e la trasformazione corrisponde all’identità: $$ \begin{cases} x' = x \\ y' = y \end{cases} $$

Dimostrazione

Vediamo come si dimostra la formula di rotazione.

Considero un punto P(x;y) del piano e traccio il segmento $ \overline{OP} $ che congiunge l'origine O con il punto P.

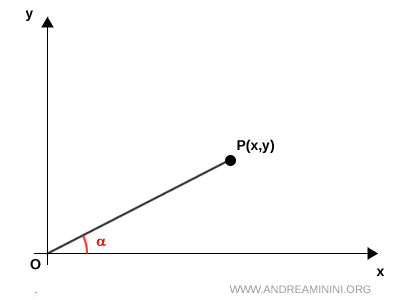
Questo segmento forma un angolo $ \alpha $ rispetto al semiasse positivo delle ascisse.

Le coordinate del punto $ P $ si esprimono come:

$$ x = \overline{OP} \cdot \cos \alpha $$

$$ y = \overline{OP} \cdot \sin \alpha $$

Dove per $ \overline{OP} $ intendo la lunghezza del segmento, ossia la distanza tra i punti $ O $ e $ P $.

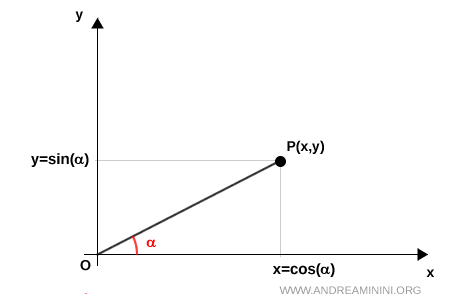
A questo punto, ruoto il segmento $ \overline{OP} $ di un angolo $ \beta $ in senso antiorario con centro di rotazione $ O $

Dopo la rotazione il punto trasformato si trova alle coordinate $ P'(x',y') $

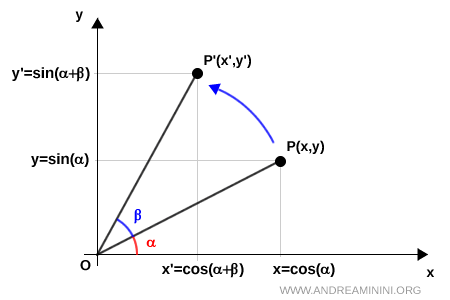
Le componenti del punto trasformato sono le seguenti:

$$ x' = \overline{OP'} \cdot \cos ( \alpha + \beta ) $$

$$ y' = \overline{OP'} \cdot \sin ( \alpha + \beta ) $$

Ora applico le formule di addizione del seno e del coseno.

$$ x' = \overline{OP'} \cdot [ \cos ( \alpha ) \cos ( \beta ) - \sin ( \alpha) \sin{ \beta } ] $$

$$ y' = \overline{OP'} \cdot [ \sin ( \alpha ) \cos (\beta ) + \cos ( \alpha ) \sin ( \beta ) ]  $$

Svolgo i prodotti.

$$ x' = \overline{OP'}  \cos ( \alpha ) \cos ( \beta ) -  \overline{OP'} \sin ( \alpha) \sin{ \beta }  $$

$$ y' = \overline{OP'} \sin ( \alpha ) \cos (\beta ) +  \overline{OP'} \cos ( \alpha ) \sin ( \beta )  $$

I segmenti $ \overline{OP} \cong \overline{OP'} $ sono congruenti perchè la rotazione è un'isometria, quindi posso sostituire $ \overline{OP'} $ con $ \overline{OP} $

$$ x' = \overline{OP}  \cos ( \alpha ) \cos ( \beta ) -  \overline{OP} \sin ( \alpha) \sin{ \beta }  $$

$$ y' = \overline{OP} \sin ( \alpha ) \cos (\beta ) +  \overline{OP} \cos ( \alpha ) \sin ( \beta )  $$

Sapendo che $ x= \overline{OP} \cos ( \alpha ) $ e $ y = \overline{OP} \sin ( \alpha ) $

$$ x' = \underbrace{ \overline{OP}  \cos ( \alpha ) }_{x} \cos ( \beta ) -  \underbrace{ \overline{OP} \sin ( \alpha) }_{y} \sin{ \beta }  $$

$$ y' = \underbrace{  \overline{OP} \sin ( \alpha ) }_{y} \cos (\beta ) + \underbrace{  \overline{OP} \cos ( \alpha ) }_{x} \sin ( \beta )  $$

Quindi

$$ x' =  x \cos ( \beta ) - y \sin{ \beta }  $$

$$ y' =  y \cos (\beta ) + x \sin ( \beta )  $$

Riordino i termini per $ x $ e $ y $ diventa:

$$ x' =  x \cos ( \beta ) - y \sin{ \beta }  $$

$$ y' =  x \sin ( \beta ) + y \cos (\beta )   $$

Ho così dimostrato le equazioni della rotazione di un punto intorno all'origine con un angolo $ \beta $.

Nota. Per calcolare le coordinate originali di un punto dopo una rotazione inversa, è sufficiente considerare una rotazione di angolo orientato negativo $-\beta$. Le formule diventano: $$ \begin{aligned}x &= x' \cos(-\beta) - y' \sin(-\beta) \\ y &= x' \sin(-\beta) + y' \cos(-\beta) \end{aligned}$$ Sfruttando le identità goniometriche $ \cos(-\beta) = \cos(\beta) $ e $ \sin(-\beta) = -\sin(\beta) $ si ottengono le equazioni della rotazione inversa: $$ \begin{aligned}x &= x' \cos \beta + y' \sin \beta \\ y &= -x' \sin \beta + y' \cos \beta\end{aligned} $$

La rotazione rispetto a un centro qualsiasi

La rotazione di un punto rispetto a un centro di rotazione (x₀, y₀) diverso dall'origine degli assi si realizza usando questa formula $$ \begin{cases} x' = (x - x_0) \cdot \cos \alpha - (y - y_0) \cdot \sin \alpha + x_0 \\ \\ y' = (x - x_0) \cdot \sin \alpha + (y - y_0) \cdot \cos \alpha + y_0 \end{cases} $$

In altre parole, per ruotare un punto attorno a un centro di rotazione diverso dall'origine, ovvero un punto (x₀, y₀), devo prima traslare il sistema in modo che (x₀, y₀) diventi l'origine.

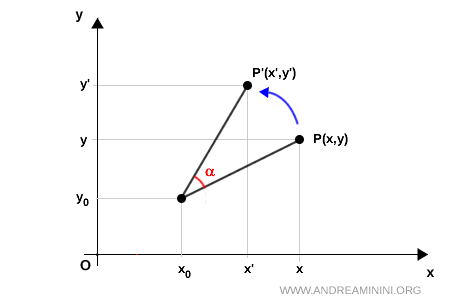
Poi applicare la rotazione, e infine traslare indietro al sistema originale.

1. Traslazione alla nuova origine (x₀, y₀) $$ x_{temp} = x-x_0 \\ y_{temp} = y-y_0 $$
2. Rotazione attorno all'origine sul punto traslato $$ \begin{cases} x'_{temp} = x_{temp} \cdot \cos \alpha - y_{temp} \cdot \sin \alpha \\ y'_{temp} = x_{temp} \cdot \sin \alpha + y_{temp} \cdot \cos \alpha \end{cases} $$
3. Traslazione indietro al sistema originale $$ x' = x'_{temp} + x_0 \\ y' = y'_{temp} + y_0 $$

La combinazione di queste trasformazioni geometriche mi permette di ottenere le formule per la rotazione attorno a un punto arbitrario (x₀, y₀) qualsiasi.

$$ \begin{cases} x' = (x - x_0) \cdot \cos \alpha - (y - y_0) \cdot \sin \alpha + x_0 \\ \\ y' = (x - x_0) \cdot \sin \alpha + (y - y_0) \cdot \cos \alpha + y_0 \end{cases} $$

Questa formula rappresenta la regola generale per la rotazione nel piano ed è applicabile in qualsiasi situazione.

Ad esempio, se prendo come centro di rotazione il punto x₀=0 e y₀=0, la formula si riduce a quella della rotazione attorno all'origine degli assi.

Esempio. In questo esempio devo far ruotare il punto A=(2;3) di 45° in senso antiorario (+45°) rispetto al punto O'=(1;1) e non rispetto all'origine degli assi O=(0;0). Applico la formula di rotazione precedente. $$ \begin{cases} x' = (x - x_0) \cdot \cos \alpha - (y - y_0) \cdot \sin \alpha + x_0 \\ \\ y' = (x - x_0) \cdot \sin \alpha + (y - y_0) \cdot \cos \alpha + y_0 \end{cases} $$ Sostituisco le coordinate del centro di rotazione x₀=1 e y₀=1 $$ \begin{cases} x' = (x - 1) \cdot \cos \alpha - (y - 1) \cdot \sin \alpha + 1 \\ \\ y' = (x - 1) \cdot \sin \alpha + (y - 1) \cdot \cos \alpha + 1 \end{cases} $$ Sostituisco le coordinate del punto A, quello che voglio far ruotare, ossia x=2 e y=3 $$ \begin{cases} x' = (2 - 1) \cdot \cos \alpha - (3 - 1) \cdot \sin \alpha + 1 \\ \\ y' = (2 - 1) \cdot \sin \alpha + (3 - 1) \cdot \cos \alpha + 1 \end{cases} $$ $$ \begin{cases} x' = 1 \cdot \cos \alpha - 2 \cdot \sin \alpha + 1 \\ \\ y' = 1 \cdot \sin \alpha + 2 \cdot \cos \alpha + 1 \end{cases} $$ Sostituisco l'angolo di rotazione α=45° in senso orario. $$ \begin{cases} x' = 1 \cdot \cos 45° - 2 \cdot \sin 45° + 1 \\ \\ y' = 1 \cdot \sin 45° + 2 \cdot \cos 45° + 1 \end{cases} $$ Sapendo che il seno e il coseno di 45° sono approssimativamente sin(45°)=0,71 e cos(45°)=0,71 $$ \begin{cases} x' = 1 \cdot 0,71 - 2 \cdot 0,71 + 1 \\ \\ y' = 1 \cdot 0,71 + 2 \cdot 0,71 + 1 \end{cases} $$ $$ \begin{cases} x' = 0,71 - 1,42 + 1 \\ \\ y' = 0,71 + 1,42 + 1 \end{cases} $$ $$ \begin{cases} x' = 0,29 \\ \\ y' = 3,13 \end{cases} $$ Le nuove coordinate del punto A' dopo la rotazione sono x'=0,29 e y=3,13.

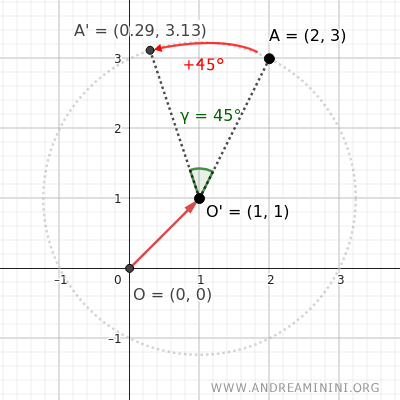
La rotazione nello spazio

Per ruotare un solido nello spazio scelgo una retta \( r \), detta asse di rotazione, un piano perpendicolare \( \pi \) alla retta e un angolo di rotazione \( \alpha \).

La trasformazione fa corrispondere ogni punto \( P \) del solido a un punto associato \( P' \) che appartiene allo stesso piano \( \pi \).

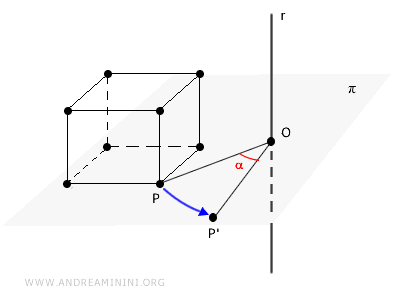
I punti della retta \( r \) rimangono invarianti (detti punti uniti), ossia mantengono la stessa posizione in qualsiasi rotazione.

Ogni altro punto del solido, invece, si muove su una circonferenza contenuta nel piano \( \pi \), avente come centro il punto \( O \) sull'asse \( r \), quello che interseca il piano, e raggio pari alla distanza \( \overline{OP} \) tra \( P \) e \( r \).

La nuova posizione di \( P' \) è determinata dall'angolo di rotazione \( \alpha \), che misura la rotazione rispetto al centro \( O \) della circonferenza.

Osservazioni

Alcune osservazioni sulla rotazione

• La rotazione è una isometria
  Se prendo due punti A e B qualsiasi e i loro trasformati A' e B', la rotazione non modifica la distanza tra i punti. In altre parole i segmenti AB≅A'B' sono congruenti.
  

  Dimostrazione. Considero due punti qualsiasi $A$ e $B$ nel piano, e un punto fisso $O$. Applico una rotazione di centro $O$ e angolo $ \theta$, ottenendo i punti $A'$ e $B'$.
  
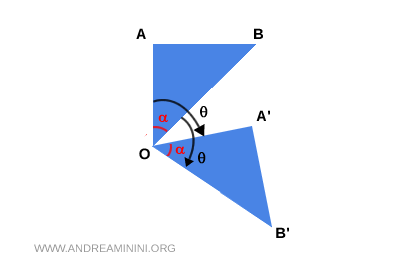
  Poiché la rotazione conserva le distanze dal centro, i segmenti $ OA \cong OA' $ e $ OB = OB' $ sono congruenti. Inoltre, la rotazione preserva gli angoli, quindi anche gli angoli $ \angle AOB = \angle A'OB' $ sono congruenti. Di conseguenza, i triangoli $OAB$ e $OA'B'$ hanno due lati corrispondenti congruenti e l’angolo compreso congruente, quindi sono triangoli congruenti secondo il criterio Lato-Angolo-Lato (LAL). Pertanto, anche il terzo lato è congruente $ AB = A'B' $. Poiché $AB$ è la distanza tra i punti originali e $A'B'$ è la distanza tra le loro immagini, questo dimostra che la rotazione conserva le distanze tra i punti, ossia la rotazione è un’isometria.

• Una rotazione di ampiezza nulla o multipla di 360° è un'identità
  Nel piano una rotazione di 0° o multipla di un angolo giro (360°) nel piano equivale all'operazione identità. Questo perché una rotazione di questa ampiezza non modifica la posizione della figura. In altre parole, una rotazione nulla o, in generale, multipla n volte di un angolo giro produce una figura unita sul piano. 
  

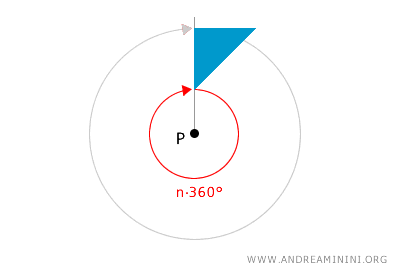
  Una figura si dice "unita" se tutti i suoi punti mantengono la stessa posizione sul piano dopo una trasformazione geometrica.

• In una rotazione il centro di rotazione è un punto unito
  In qualsiasi rotazione, il centro di rotazione P non modifica mai la sua posizione sul piano. Quindi, il centro di rotazione è sempre un punto unito.
  

  Un punto si dice "unito" se mantiene la stessa posizione sul piano dopo una trasformazione geometrica.

• La circonferenza e il cerchio sono figure unite rispetto a qualsiasi rotazione intorno al loro centro
  In qualsiasi rotazione intorno al loro centro, la circonferenza e il cerchio non modificano la loro posizione sul piano.
• Il quadrato è una figura unita rispetto a una rotazione intorno al suo centro per angoli multipli di un angolo retto
  Il quadrato non modifica la sua posizione sul piano dopo una rotazione intorno al suo centro, il punto di intersezione tra le diagonali, per un angolo multiplo di un angolo retto (90°).
• Nel piano una rotazione di ±180° coincide con la simmetria centrale
  La rotazione di 180° (angolo piatto) attorno a un punto P coincide con la simmetria centrale rispetto allo stesso punto P. Quando si ruota una figura di 180° attorno a un punto, ogni punto della figura si sposta in una posizione diametralmente opposta rispetto al centro di rotazione, mantenendo la stessa distanza da P. Questo comportamento è esattamente quello che si verifica con la simmetria centrale: ogni punto viene mappato in un punto diametralmente opposto rispetto al centro di simmetria. Pertanto, una rotazione di ±180° ( ±π radianti ) e una simmetria centrale rispetto allo stesso punto sono trasformazioni geometriche equivalenti. La rotazione di ±180° è anche detta "opposizione" o "semigiro".
  
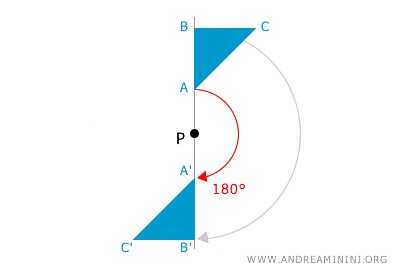
• Nello spazio una rotazione nello spazio di 180° coincide con la simmetria assiale
  Nello spazio, una rotazione di 180° corrisponde alla simmetria assiale. Questo significa che, quando un oggetto tridimensionale viene ruotato di 180° attorno a un asse, ogni punto dell'oggetto si riflette rispetto a tale asse, risultando in una posizione simmetrica. È come se l'oggetto fosse stato "ribaltato" attorno all'asse di rotazione.
• La composizione delle rotazioni
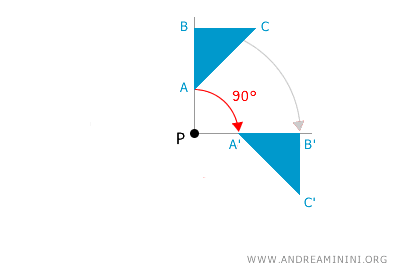
  La composizione di due o più rotazioni r(P;α) e r(P;β) con lo stesso centro di rotazione P equivale a una singola rotazione con centro P e un angolo pari alla somma algebrica degli angoli di rotazione α e β, ovvero r(P; α+β).
  

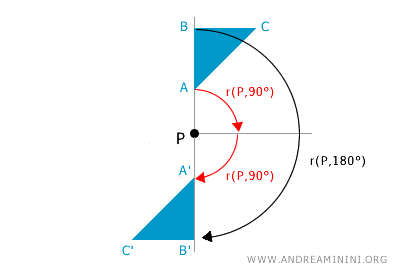
  In generale la composizione delle rotazioni non è un'operazione interna alle rotazioni, perché se il centro di rotazione è diverso, non è detto che la composizione di due o più rotazioni sia ancora equivalente a una singola rotazione. Ecco un esempio di composizione di due rotazioni della stessa figura ma con centro di rotazione differente P e P'
  
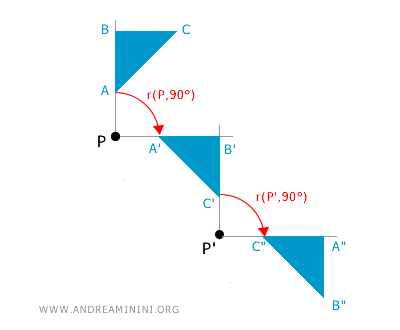
  La composizione di due rotazioni di angoli $\alpha_1$ e $\alpha_2$ con centri diversi $ P $ e $ P' $ può essere una rotazione con un centro diverso e angolo $\alpha_1 + \alpha_2$, oppure una traslazione. Quindi, la composizione di rotazioni con centri diversi non è, in generale, una rotazione. Viceversa, la composizione di due rotazioni di angoli $\alpha_1$ e $\alpha_2$ con lo stesso centro $ P $ è ancora una rotazione con centro $ P $ e angolo $\alpha_1 + \alpha_2$.  

• Le rotazioni nel piano con lo stesso centro formano un gruppo commutativo
  Quando combino due rotazioni consecutive nel piano con lo stesso centro di rotazione P, il risultato è sempre un'altra rotazione con lo stesso centro. Quindi, la rotazione sul piano è un'operazione chiusa perché il risultato appartiene allo stesso insieme di rotazioni. L'ordine in cui applico le rotazioni non influisce sul risultato finale. In altre parole, ruotare di α gradi seguito da β gradi è equivalente a ruotare di β gradi seguito da α gradi. Pertanto, la rotazione sul piano soddisfa la proprietà commutativa. Per questa ragione le rotazioni nel piano formano un gruppo commutativo (gruppo abeliano).
• Il determinante della matrice di rotazione è sempre 1
  La matrice di rotazione nel piano, per un angolo $\alpha$, è la seguente: $$  R(\alpha) = \begin{pmatrix}
  \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{pmatrix} $$ Il determinante di questa matrice si calcola come: $$ \det(R(\alpha)) = \cos \alpha \cdot \cos \alpha - (-\sin \alpha) \cdot \sin \alpha $$ $$ \det(R(\alpha))  = \cos^2 \alpha + \sin^2 \alpha = 1 $$ Il risultato finale è l'identità trigonometrica fondamentale $ \cos^2 \alpha + \sin^2 \alpha  = 1 $  Quindi, il determinante della matrice di rotazione è sempre 1, per qualunque angolo $\alpha$.

  Nota.Questo riflette il fatto che la rotazione è una trasformazione isometrica (cioè conserva le distanze) e preserva le aree perché il determinante è ±1, in questo caso +1, quindi senza inversione. Inoltre, la rotazione preserva l'orientamento, a differenza di una riflessione che avrebbe determinante -1.

E così via.