Composizione di trasformazioni geometriche

La composizione di trasformazioni geometriche è l'applicazione di due o più trasformazioni in sequenza allo stesso oggetto. $$ s \circ t $$

Si legge "s composto t", dove "t" è la prima trasformazione mentre "s" è la seconda trasformazione. Quindi, la composizione si legge da destra verso sinistra.

Un esempio pratico

Ad esempio, considero una figura geometrica iniziale.

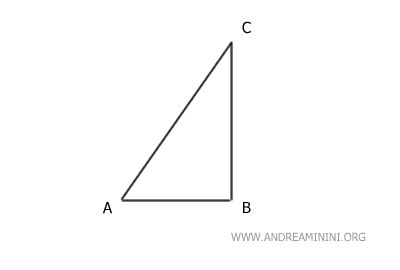
Come prima trasformazione geometrica applico una rotazione di 90° intorno al centro di rotazione A.

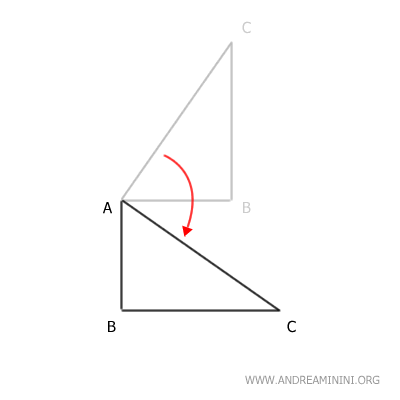
Poi applico al risultato la seconda trasformazione geometrica. Ad esempio, una traslazione in avanti rispetto al segmento AB.

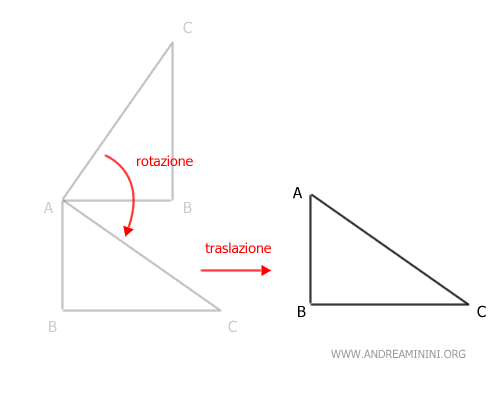
Il risultato finale è la composizione di due trasformazioni geometriche.

Nota. Una trasformazione geometrica consiste nel modificare una figura secondo determinate regole, senza alterarne alcune proprietà fondamentali. Sono trasformazioni geometriche le traslazioni, rotazioni, riflessioni e dilatazioni.

E' utile sottolineare che la composizione delle trasformazioni geometriche non soddisfa la proprietà commutativa.

Quindi, è fondamentale prestare attenzione all'ordine in cui le trasformazioni vengono applicate, poiché questo può influenzare notevolmente il risultato finale.

La composizione delle trasformazioni nello spazio

Le composizioni delle trasformazioni geometriche si applicano anche alle figure solide nello spazio.

Quando applico una trasformazione geometrica a una figura, ottengo una nuova figura trasformata. Se poi applico un'altra trasformazione a questa nuova figura, ottengo un'altra trasformazione finale.

Esempio

Prendo una figura nello spazio \( \mathcal{F} \), ad esempio una piramide con base quadrata, e applico una traslazione come prima trasformazione \( t_1 \). Ora ho un nuovo solido \( \mathcal{F}_1 \).

Poi applico una simmetria rispetto a un piano come seconda trasformazione \( t_2 \) e ottengo un nuovo solido \( \mathcal{F}_2 \).

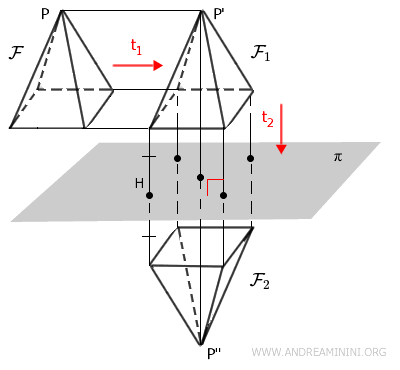
Questa combinazione è un esempio di trasformazione composta \( t_2 \circ t_1 \) nello spazio, dove si applica prima \( t_1 \) e poi \( t_2 \)..

Quindi, invece di fare i due passaggi separati, posso applicare direttamente la trasformazione \( t_2 \circ t_1 \) al solido iniziale \( \mathcal{F} \) per ottenere il solido finale \( \mathcal{F}_2 \).

Nota. Anche nello spazio, l'ordine delle trasformazioni geometriche è fondamentale perché, in generale, la composizione non è commutativa. Questo significa che applicare due trasformazioni in ordine diverso può portare a risultati differenti.

La composizione delle trasformazioni in geometria analitica

Date due trasformazioni $t_1$ e $t_2$, la trasformazione composta $t_2 \circ t_1$ è definita come:$$(t_2 \circ t_1)(P) =  _2(t_1(P))$$ Dove $ P $ è un punto qualsiasi.

In altre parole, si applica prima la trasformazione più interna $t_1$ al punto $P$, ottenendo il punto $P_1 = t_1(P)$, e poi si applica la trasformazione $t_2$ a $P_1$, ottenendo il punto finale $P_2 = t_2(P_1)$.

Quindi, se $t_1: (x, y) \mapsto (x', y')$ e $t_2: (x', y') \mapsto (x'', y'')$, allora la trasformazione composta $t_2 \circ t_1$ è:

$$ t_2 \circ t_1 : (x, y) \mapsto (x'', y'') = t_2(t_1(x, y)) $$

Come giù anticipato, in generale la composizione non è commutativa e l’ordine con cui si applicano le trasformazioni è fondamentale.

$$ t_2 \circ t_1 \ne t_1 \circ t_2 $$

E' invece valida la proprietà associativa

$$ t_1 \circ ( t_2 \circ t_3 ) = ( t_1 \circ t_2 ) \circ t_3 $$

La proprietà associativa afferma che l'ordine con cui raggruppo le trasformazioni non cambia il risultato.

Se prima compongo $t_2$ con $t_3$ e poi applico $t_1$, oppure prima compongo $t_1$ con $t_2$ e poi applico il risultato a $t_3$, ottengo lo stesso effetto complessivo.

Nota. Nel caso particolare di una trasformazione composta tra una trasformazione $ t_1 $ e la sua inversa $ t_1^{-1} $, il risultato finale è la trasformazione identica, ossia una identità, che lascia invariati tutti i punti del piano: $$ t_1 \circ t_1^{-1} = t_1{-1} \circ t_1 = i $$ In questo caso specifico, la proprietà commutativa risulta soddisfatta.

Esempio

Considero le seguenti due trasformazioni nel piano cartesiano:

La trasformazione $t_1$ è una riflessione rispetto all’asse $x$

$$
t_1: \begin{cases}
x' = x \\
y' = -y
\end{cases}
$$

La trasformazione $t_2$ è una traslazione di 2 unità verso destra e 3 verso l’alto.

$$
t_2: \begin{cases}
x'' = x' + 2 \\
y'' = y' + 3
\end{cases}
$$

Prendo come punto di partenza il punto $A(1, -4)$ del piano.

Svolgo la composizione $t_2 \circ t_1$, cioè prima $t_1$, poi $t_2$.

Applico la prima trasformazione $ t_1: \begin{cases}
x' = x \\
y' = -y
\end{cases} $ al punto $ A(1,-4) $

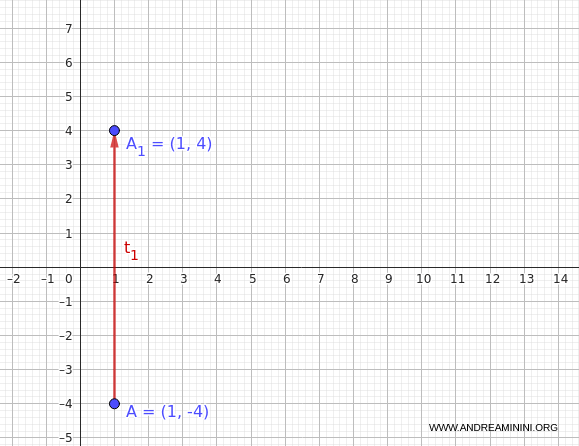
In questo modo ottengo il punto $ A_1(1,4) $

$$ A_1 = t_1(1, -4) = (1, 4) $$

Ecco cosa accade sul piano

Poi applico la seconda trasformazione $t_2: \begin{cases}
x'' = x' + 2 \\
y'' = y' + 3
\end{cases} $ al punto $A_1(1,4) $

Quindi, ottengo il punto $ A_2(3,7) $

$$ A_2 = t_2(1, 4) = (1 + 2, 4 + 3) = (3, 7) $$

Ecco il risultato dal punto di vista grafico

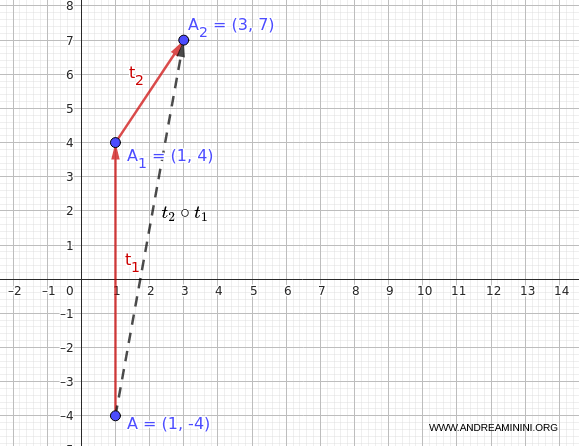
Quindi, la trasformazione composta $t_2 \circ t_1$ applicata ad $A$ dà come risultato il punto $ (3,7) $:

$$ (t_2 \circ t_1)(A) = (3, 7) $$

Nota. Unendo le due trasformazioni in un’unica formula, posso scrivere la trasformazione composta come un'unica trasformazione $$ t_2 \circ t_1 :  \begin{cases} x'' = x + 2 \\ y'' = -y + 3 \end{cases} $$

Esempio 2

Riprendo lo stesso esempio le stesse trasformazioni e lo stesso punto iniziale $ A(1, -4) $

$$
t_1: \begin{cases}
x' = x \\
y' = -y
\end{cases}
$$

$$
t_2: \begin{cases}
x'' = x' + 2 \\
y'' = y' + 3
\end{cases}
$$

Questa volta, però, calcolo la trasformazione composta nell’altro ordine

$$t_1 \circ t_2$$

Cioè prima $t_2$, poi $t_1$.

Applico la prima trasformazione $t_2 : \begin{cases}
x'' = x' + 2 \\
y'' = y' + 3
\end{cases} $ al punto $A(1, -4)$

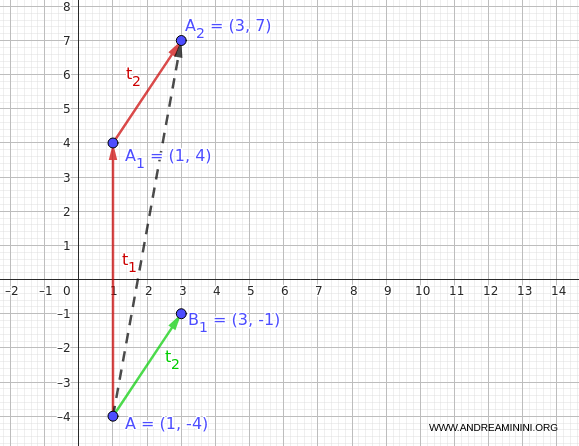
In questo modo ottengo il punto $ B_1(3, -1) $

$$ t_2(1, -4) = (1 + 2, -4 + 3) = (3, -1) $$

Ecco il risultato intermedio sul piano, lo disegno con il verde per distinguerlo dalla precedente trasformazione in rosso.

Poi applico la seconda trasformazione $t_1: \begin{cases}
x' = x \\
y' = -y
\end{cases}$ al risultato al punto $ B_1(3, -1) $

Così facendo ottengo il punto $ B_2(3, 1) $

$$ t_1(3, -1) = (3, 1) $$

Ecco il risultato grafico della composizione (verde)

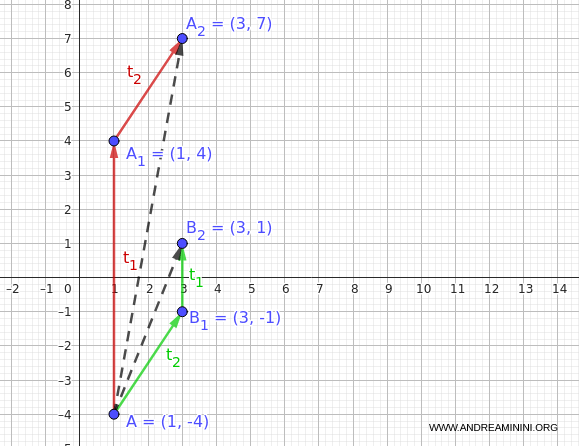
Quindi, la trasformazione composta $ (t_1 \circ t_2)(A) $ conduce al punto $ (3,1) $.

$$ (t_1 \circ t_2)(A) = (3, 1) $$

Nota. Le due composizioni (rossa e verde) restituiscono risultati diversi: $$(t_2 \circ t_1)(A) = (3, 7)$$ $$(t_1 \circ t_2)(A) = (3, 1)$$ Questo conferma che in generale la trasformazione composta non soddisfa la proprietà commutativa $$ t_2 \circ t_1 \ne t_1 \circ t_2 $$

Esempio 3

Considero la trasformazione $t_1$ che trasla un punto di +4 sull'asse x e di -2 sull'asse y.

$$
t_1: \begin{cases}
x' = x + 4 \\
y' = y - 2
\end{cases}
$$

La sua trasformazione inversa $t_1^{-1}$ deve "annullare" gli effetti di $t_1$.

$$
t_1^{-1}: \begin{cases}
x'' = x' - 4 \\
y'' = y' + 2
\end{cases}
$$

Compongo le due trasformazioni:

$$t_1^{-1} \circ t_1$$

Poi prendo un punto qualsiasi:

$$ P(3, 5) $$

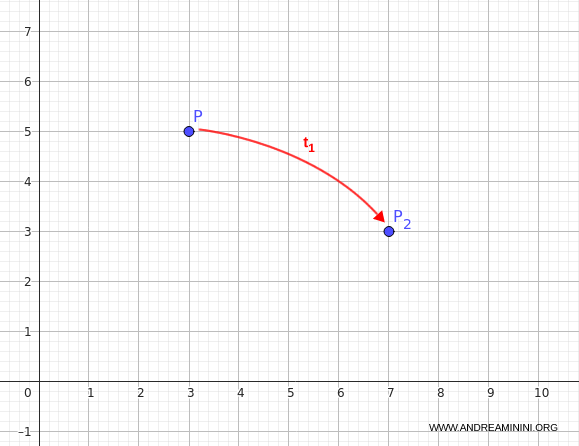
Per eseguire la composizione $t_1^{-1} \circ t_1$ applico prima $t_1$ al punto $ P(3,5) $

In questo modo ottengo il punto $ P_2(7,3) $

$$ t_1(3, 5) = (3 + 4, 5 - 2) = (7, 3) $$

Ecco il risultato sul piano

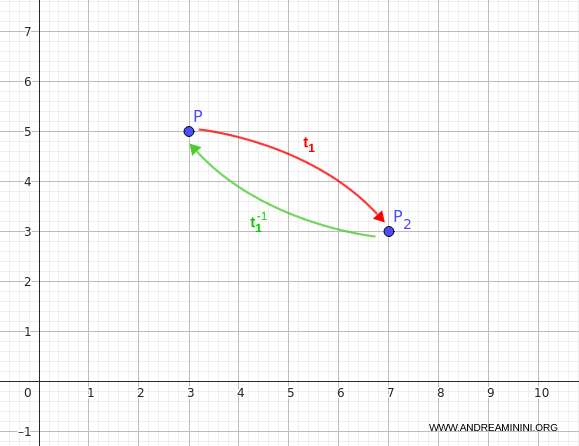
Poi applico la trasformazione inversa $t_1^{-1}$ al risultato:

$$ t_1^{-1}(7, 3) = (7 - 4, 3 + 2) = (3, 5) $$

Ecco il risultato grafico.

Quindi la trasformazione composta riporta al punto iniziale.

$$ (t_1^{-1} \circ t_1)(3, 5) = (3, 5) $$

Questo conferma che la composizione di una trasformazione con la sua inversa restituisce il punto di partenza, cioè si ottiene la trasformazione identica, che lascia invariati tutti i punti del piano.

$$ t_1^{-1} \circ t_1 = \text{id} $$

E così via