Punto unito
Un punto si dice punto unito (o punto fisso) rispetto a una trasformazione geometrica se la sua posizione rimane invariata dopo l'applicazione della trasformazione.
In altre parole, se dopo la trasformazione geometrica il punto mantiene le stesse coordinate iniziali, allora è detto punto unito della trasformazione.
Formalmente, dato un'applicazione \( T: \mathbb{R}^2 \to \mathbb{R}^2 \), un punto \( P \) si dice unito se \( T(P) = P \), ossia se il punto ha come immagine se stesso.
Ad esempio, in una rotazione sul piano il punto centrale \( P \) della rotazione è un punto fisso, perché conserva le stesse coordinate iniziali dopo la trasformazione geometrica.
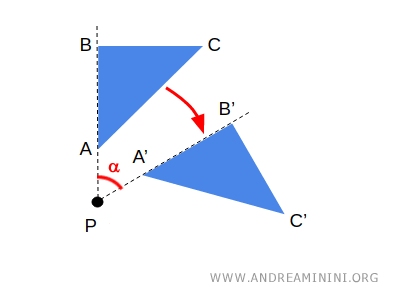
I punti uniti possono anche essere più di uno.
Ad esempio, nella simmetria rispetto a una retta \( r \), tutti i punti dell'asse di simmetria \( r \) sono uniti.
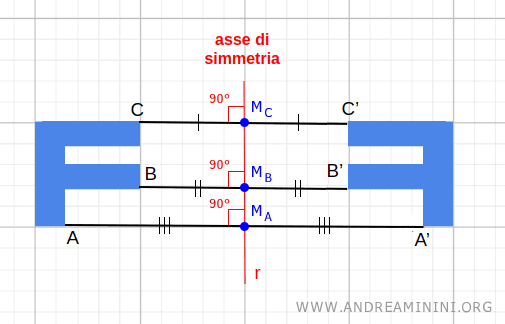
Può anche capitare che tutti i punti siano uniti in una trasformazione.
Ad esempio, una rotazione completa di 360° di una figura piana intorno a un punto centrale \( P \) non modifica le coordinate di nessun punto della figura.
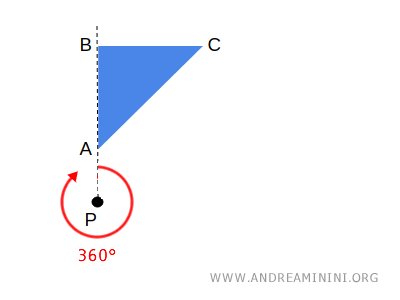
In questo caso tutti i punti sono uniti e la stessa figura geometrica è detta puntalmente unita della trasformazione.
Quando tutti i punti di una figura sono punti fissi, la trasformazione geometrica è detta identità.
Nota. Può anche capitare che alcuni punti corrispondano ad altri punti della figura. In questi casi non si parla di punti uniti. Ad esempio, se considero una retta $ y = x $ e la trasformazione geometrica $$ T: \begin{cases} x'=x+1 \\ y'=y+1 \end{cases} $$ Ogni punto della figura trasformata coincide con un altro punto della retta di origine pur non essendo un punto fisso.
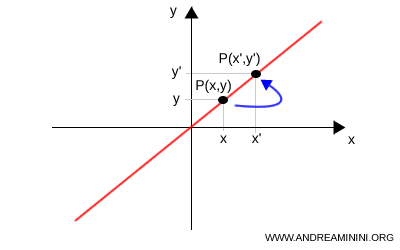
Da notare che in questo caso la figura è una figura unita per isometria perché è invariata, la distanza tra due punti qualsiasi è sempre la stessa, ma i punti non sono punti fissi della trasformazione geometrica.
Ci sono anche casi in cui nessun punto mantiene la sua posizione, quindi nessun punto è unito.
Ad esempio, nella traslazione nessun punto è unito a meno che sia la traslazione nulla.
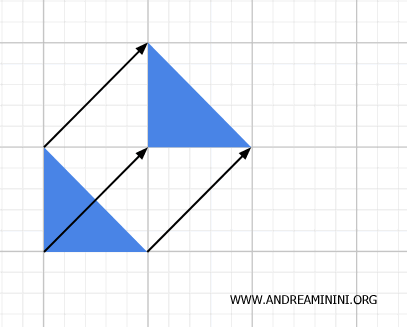
Questi sono solo alcuni esempi pratici di punti fissi di una trasformazione geometrica.
Nota. Il concetto di punto unito o punto fisso di una trasformazione geometrica si estende dallo spazio bidimensionale al tridimensionale senza variazioni nella definizione. Un punto è detto fisso se mantiene invariate le proprie coordinate dopo l'applicazione della trasformazione. L'unica differenza nello spazio tridimensionale è il numero di coordinate che descrivono un punto, che passano da due \((x, y)\) a tre \((x, y, z)\).
E così via.
