Trasformazioni affini
Una trasformazione affine (o di affinità) è una trasformazione geometrica che conserva l’allineamento dei punti e il parallelismo delle rette, ma non necessariamente le lunghezze e gli angoli.
In altre parole, una trasformazione affine può traslare, ruotare, scalare, riflettere o deformare una figura, purché le linee rette rimangano rette e quelle parallele rimangano parallele, i rapporti di allineamento tra punti sono mantenuti.
L'allineamento dei punti e il parallelismo sono gli invarianti della trasformazione affine.
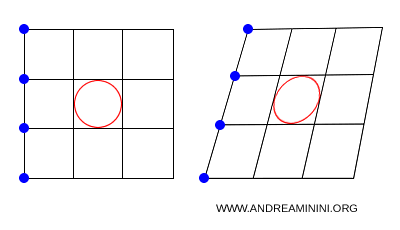
In generale, le lunghezze, gli angoli e le aree non necessariamente si conservano.
Anche la forma non è un invariante dell'affinità. Ad esempio, un triangolo rettangolo può trasformarsi in un triangolo acutangolo o ottusangolo.
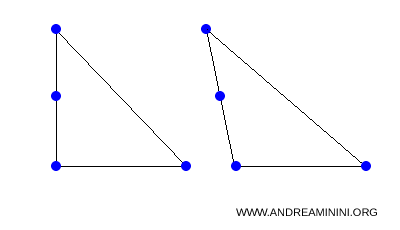
Dal punto di vista matematico l'affinità è un tipo di funzione che mappa punti, linee e figure su un piano o uno spazio in un altro piano o spazio, mantenendo le rette parallele tra loro.
$$ \mathbf{y} = A\mathbf{x} + \mathbf{b} $$
Dove \( \mathbf{x} \) è il vettore delle coordinate iniziali (prima della trasformazione), \( A \) è una matrice che rappresenta la parte lineare della trasformazione (rotazioni, dilatazioni, riflessioni, ecc.), \( \mathbf{b} \) è un vettore di traslazione che sposta tutta la figura.
Ecco alcuni esempi di trasformazioni affini
- Traslazione: se \( A = I \) (matrice identità) e \( \mathbf{b} \neq 0 \)
- Rotazione: se \( A \) è una matrice di rotazione e \( \mathbf{b} = 0 \)
- Omotetia (scalatura) se \( A = k \cdot I \) (matrice identità)
Le trasformazioni affini possono essere isometriche oppure no, ovvero mantenere le lunghezze e gli angoli o meno. Quello che resta comunque invariato è il parallelismo e l'allineamento dei punti.
Un esempio pratico
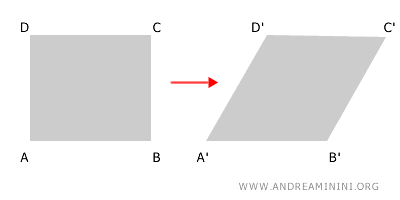
Esempio 1 (affinità non isometrica)
Questa trasformazione geometrica è affine perché viene conservato il parallelismo tra le rette e l'allineamento dei punti.
Si tratta di una trasformazione affine non isometrica, in quanto non viene mantenuta la congruenza, variano le ampiezze degli angoli e le lunghezze dei segmenti.
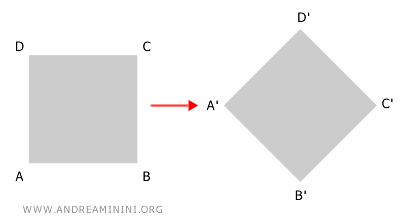
Esempio 2 (affinità isometrica)
Questo è, invece, un esempio di affinità isometrica. Consiste nella composizione di una traslazione e di una rotazione.
In questo caso viene conservato sia il parallelismo tra le rette e l'allineamento dei punti che la congruenza tra le lunghezze e gli angoli corrispondenti.
Il rapporto di affinità
In una trasformazione affine il rapporto tra le aree di due figure corrispondenti è costante. $$ \frac{A_{S'}}{A_S} = k $$ Dove $ S $ una figura piana e $ S' $ la sua immagine affine. Il valore \( k \) è detto rapporto di affinità.
Se $ k = 1 $, allora $ A_{S'} = A_S $ e la trasformazione conserva le aree.
Le trasformazioni affini che conservano le aree si chiamano equiaffinità o equivalenze affini.
Esempio
Considero il quadrato \(S\) di lato 2, quindi con area
\( A_S = 2^2 = 4. \)
Applico una trasformazione affine che dilata le coordinate orizzontali del doppio e lascia invariate quelle verticali. In forma analitica la trasformazione è:
\[ \begin{cases} x' = 2x \\ \\ y' = y \end{cases} \]
La nuova figura \(S'\) è un rettangolo con base 4 e altezza 2, quindi la sua area è:
\( A_{S'} = 4 \times 2 = 8. \)
Da ciò risulta:
\[ \frac{A_{S'}}{A_S} = \frac{8}{4} = 2 = k. \]
Il rapporto di affinità è quindi \(k = 2\).
Nota. Se invece la trasformazione fosse stata una semplice rotazione o traslazione (senza variazione di scala), si avrebbe \(k = 1\) e l’area sarebbe rimasta invariata, cioè l’affinità sarebbe equiaffine.
Le equazioni dell'affinità
Nella geometria analitica l'affinità può essere ottenuta usando un sistema di equazioni che associa a ogni punto \( (x, y) \) un nuovo punto \( (x', y') \) tramite due equazioni lineari:
\[
\begin{cases}
x' = a x + b y + c \\ \\
y' = a' x + b' y + c'
\end{cases}
\]
I coefficienti \( a, b, a', b' \) determinano come il piano viene deformato (rotazioni, dilatazioni, inclinazioni, ecc.), mentre \( c \) e \( c' \) spostano la figura, cioè rappresentano una traslazione.
La condizione \( ab' - a'b \neq 0 \) significa che il determinante della matrice è diverso da zero.
\[ \begin{pmatrix} a & b \\ a' & b' \end{pmatrix} \ne 0 \]
Questo è fondamentale perché assicura che la trasformazione sia invertibile, cioè che a ogni punto del piano corrisponda uno e un solo punto trasformato, e viceversa.
A seconda del segno del determinante l'affinità può essere diretta o indiretta
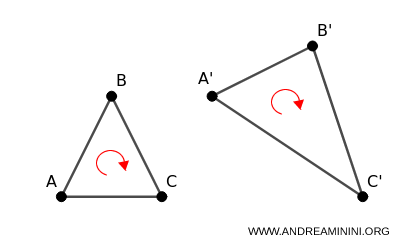
- Affinità diretta
Se il segno del determinante è maggiore di zero l'affinità conserva l'orientamento dei vertici $ A, B, C $ ed è detta "diretta". \[ \begin{pmatrix} a & b \\ a' & b' \end{pmatrix} > 0 \]
- Affinità indiretta
Se il segno del determinante è minore di zero l'affinità inverte l'orientamento dei vertici $ A, B, C $ ed è detta "indiretta". \[ \begin{pmatrix} a & b \\ a' & b' \end{pmatrix} < 0 \]
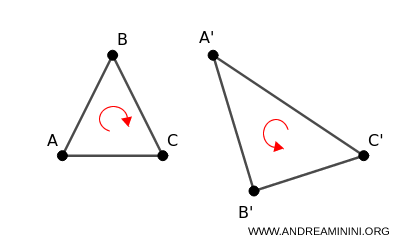
In sintesi, l’affinità diretta “deforma senza capovolgere” mentre l'affinità indiretta “deforma e capovolge”.
In altre parole, il segno del determinante funziona come un indicatore di orientamento del piano dopo la trasformazione. Un valore positivo mantiene l'orientamento del sistema di riferimento, un valore negativo la capovolge.
Esempio
Considero un triangolo con i vertici \( A(1, 1), B(2, 3), C(3, 1) \).
Applico al triangolo trasformazione affine del tipo
\[
\begin{cases}
x' = 2x + y + 1 \\ \\
y' = x + y + 2
\end{cases}
\]
Calcolo il determinante del sistema
\[
D =
\begin{vmatrix}
2 & 1 \\
1 & 1
\end{vmatrix}
= 2 \cdot 1 - 1 \cdot 1 = 1 > 0
\]
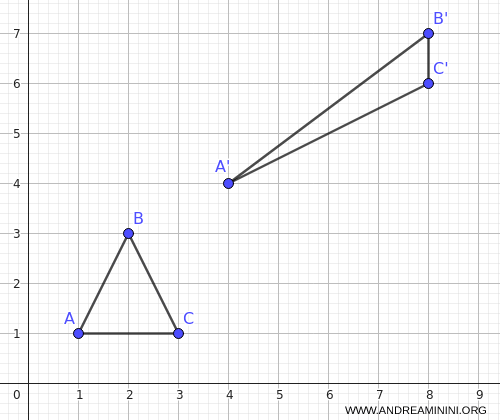
Il determinante è positivo, quindi l’affinità è diretta (conserva l’orientamento).
Ora calcolo le immagini dei tre vertici:
- Per A(1, 1) \[ x'_A = 2(1) + 1 + 1 = 4 \] \[ y'_A = 1 + 1 + 2 = 4 \] Quindi, l'immagine del punto è \( A′(4, 4) \)
- Per B(2, 3) \[ x'_B = 2(2) + 3 + 1 = 8 \] \[ y'_B = 2 + 3 + 2 = 7 \] Quindi, l'immagine è \( B′(8, 7) \)
- Per C(3, 1) \[ x'_C = 2(3) + 1 + 1 = 8 \] \[ y'_C = 3 + 1 + 2 = 6 \] Quindi, l'immagine è \( C′(8, 6) \)
Il triangolo trasformato ha quindi vertici \( A′(4, 4), B′(8, 7), C′(8, 6) \)
L’area è diversa, ma l’ordine dei vertici (e quindi l’orientamento) resta lo stesso, perché il determinante è positivo.
L’affinità ha quindi deformato e traslato il triangolo, senza invertirlo.
Esempio 2
Riparto dallo stesso triangolo \( A(1, 1), B(2, 3), C(3, 1) \)
Ora applico una trasformazione affine indiretta, cioè con determinante negativo.
\[
\begin{cases}
x' = x + 2y \\ \\
y' = 3x + y
\end{cases}
\]
Verifico il determinante:
\[
D =
\begin{vmatrix}
1 & 2 \\
3 & 1
\end{vmatrix}
= 1\cdot1 - 3\cdot2 = 1 - 6 = -5 < 0
\]
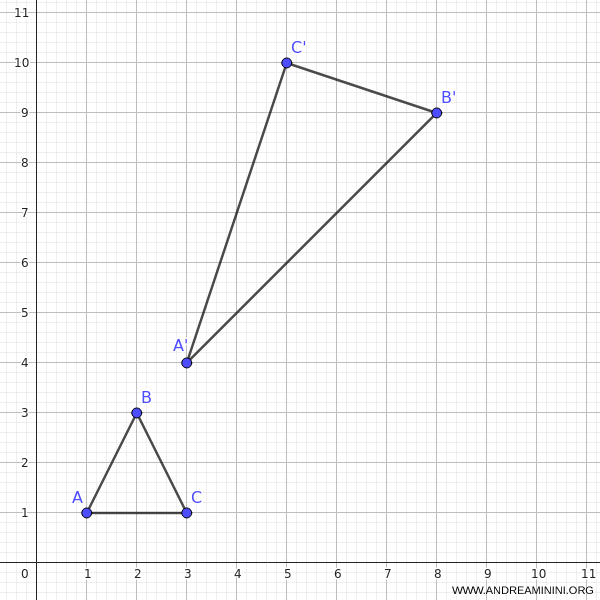
Il determinante è negativo, quindi questa affinità è indiretta, perché inverte l’orientamento.
Ora calcolo le immagini dei vertici.
- Per A(1, 1): \[ x'_A = 1 + 2(1) = 3 \] \[ y'_A = 3(1) + 1 = 4 \] Quindi, l'immagine è \( A′(3, 4) \)
- Per B(2, 3): \[ x'_B = 2 + 2(3) = 8 \] \[ y'_B = 3(2) + 3 = 9 \] Quindi, l'immagine è \( B′(8, 9) \)
- Per C(3, 1): \[ x'_C = 3 + 2(1) = 5 \] \[ y'_C = 3(3) + 1 = 10 \] Quindi, l'immagine è \( C′(5, 10) \)
Il triangolo trasformato ha quindi i vertici \( A′(3, 4), B′(8, 9), C′(5, 10) \)
Poiché il determinante è negativo, la figura risultante è ribaltata rispetto all’originale, l’ordine dei vertici (antiorario/orario) è invertito.
Punti uniti nelle affinità
In una affinità possono esistere uno, nessuno o infiniti punti uniti, ossia punti che non cambiano posizione dopo la trasformazione affine.
Le affinità con un solo punto unito si chiamano centro-affinità.
Da ciò si deduce, come corollario, che se in un’affinità esistono due punti uniti distinti, allora ce ne sono infiniti, poiché i due punti determinano una retta di punti uniti.
Dimostrazione
Considero il sistema che definisce una generica affinità:
\[
\begin{cases}
x' = a x + b y + c \\
y' = a' x + b' y + c'
\end{cases}
\]
Se un punto $ (x', y') $ è unito, allora $ x' = x $ e $ y' = y $. Sostituendo ottengo:
\[
\begin{cases}
x = a x + b y + c \\
y = a' x + b' y + c'
\end{cases}
\]
\[
\begin{cases}
a x - x + b y + c = 0 \\
a' x + b' y - y + c' = 0
\end{cases}
\]
\[
\begin{cases}
(a - 1)x + b y = -c \\
a' x + (b' - 1)y = -c'
\end{cases}
\]
Questo sistema lineare di equazioni può avere tre tipi di soluzioni:
- E' determinato, ossia ha una sola soluzione. Quindi, esiste un solo punto unito.
- E' impossibile, ossia non ha soluzioni. Quindi, non esistono punti uniti.
- E' indeterminato, cioé ha infinite soluzioni. Pertanto, esistono infiniti punti uniti.
Questo dimostra che un'affinità può avere uno, nessuno o infiniti soluzioni, ma non può avere esattamente due punti uniti. Se ci sono due o più punti uniti, allora ne seguono infiniti.
Note
Alcune note aggiunte sull'affinità geometrica
- La trasformazione affine conserva i parallelogrammi
Poiché mantiene il parallelismo tra le rette, una trasformazione affine trasforma ogni parallelogramma in un altro parallelogramma, che può risultare traslato, ruotato, dilatato o deformato, ma sempre con lati opposti paralleli. - Incidenza tra due rette
Se due rette si incontrano in un punto $ P $, allora, dopo una trasformazione affine, le loro immagini si incontrano in un punto $ P' $, che è l’immagine del punto $ P $ attraverso la trasformazione. - Coniche e trasformazioni affini
Una trasformazione affine conserva la natura delle coniche: un’ellisse viene trasformata in un’altra ellisse, una parabola in un’altra parabola e un’iperbole in un’altra iperbole. In particolare, una circonferenza, che è un caso particolare di ellisse, viene in generale trasformata in un’ellisse. - Le isometrie e le similitudini sono trasformazioni affini
Le isometrie e le similitudini rappresentano casi particolari di trasformazioni affini. In altre parole, l’insieme delle trasformazioni affini comprende come sottoinsiemi quello delle similitudini e, al suo interno, quello delle isometrie.
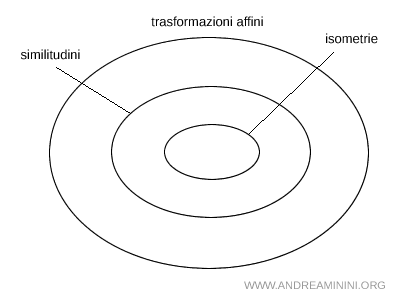
- Le dilatazioni sono affinità
Una dilatazione è un caso particolare di affinità in cui i coefficienti \( h \) e \( k \) (rapporti di dilatazione) sono entrambi diversi da zero, cioè \( h \ne 0 \) e \( k \ne 0 \). $$ \begin{cases} x' = h x + p \\ y' = k y + q \end{cases} $$ I due coefficienti \( h \) e \( k \) rappresentano i fattori di scala con cui la trasformazione modifica le lunghezze lungo gli assi coordinati. Il coefficiente \( h \) agisce lungo l'asse \( x \) mentre \( k \) lungo l'asse \( y \).Osservazione. Poiché i due coefficienti non sono nulli, anche il determinante della matrice dei coefficienti è diverso da zero e la trasformazione è quindi un’affinità: $$ \begin{vmatrix} h & 0 \\ 0 & k \end{vmatrix} = hk \ne 0 $$
- Affinità isometriche: condizioni di isometria
Un'affinità è una isometria quando sono soddisfatte le seguenti condizioni: $$ \begin{cases} a^2 + a'^2 = 1 \\ b^2 + b'^2 = 1 \\ ab + a'b' = 0 \end{cases} $$ - Affinità e similitudini: condizioni di similitudine
Un'affinità è una similitudine se sono verificate queste condizioni: $$ a^2 + a'^2 = b^2 + b'^2 $$ $$ ab+a'b' = 0 $$ In questo caso il rapporto di similitudine è: $$ k = \sqrt{a^2+a'^2}=\sqrt{b^2+b'^2} $$
E così via.
