La dilatazione e la contrazione come trasformazioni geometriche

La dilatazione è una trasformazione geometrica che associa a ogni punto P(x;y) un altro punto P'(x';y') con le seguenti coordinate geometriche $$ \begin{cases} x' = m \cdot x \\ \\ y'=n \cdot y \end{cases} $$ Dove $ m,n \in \mathbb{R}^+ $ sono due numeri reali positivi.

Quando m,n sono maggiori di 1 si ottiene una dilatazione della figura.

Viceversa, se m,n sono compresi tra 0 e 1 si ottiene una contrazione della figura.

Quindi, la contrazione è la trasformazione geometrica inversa della dilatazione.

Se n=1 si ha una dilatazione/contrazione orizzontale a seconda se m>1 oppure 0<m<1.

Se m=1 si ha una dilatazione/contrazione verticale a seconda se n>1 oppure 0<n<1

Nel caso di una funzione $ y = f(x) $ la dilatazione si può esprimere anche in questo modo $$ y = n \cdot f( \frac{x}{m} $$

Un esempio pratico

Considero quattro punti sul piano cartesiano alle coordinate A(2;2), B(4;2), C(4;4), D(2;4) come vertici di un quadrato.

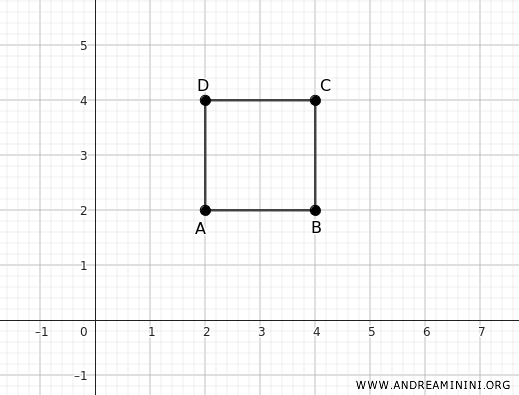
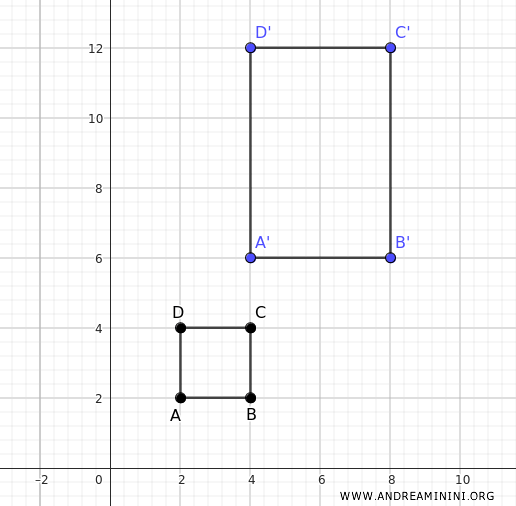
Applico una dilatazione verticale per n=2 e orizzontale per m=3

Il punto  $ A(2;2) $ diventa $ A'(4;6) $

$$ A' (2 \cdot n ; 2 \cdot m ) =  A' (2 \cdot 2 ; 2 \cdot 3 ) = A' (4; 6 ) $$

Il punto  $ B(4;2) $ diventa $ B'(8;6) $

$$ B' (4 \cdot n ; 2 \cdot m ) =  B' (4 \cdot 2 ; 2 \cdot 3 ) = B' (8; 6 ) $$

Il punto  $ C(4;4) $ diventa $ C'(8;12) $

$$ C' (4 \cdot n ; 4 \cdot m ) =  C' (4 \cdot 2 ; 4 \cdot 3 ) = C' (8; 12 ) $$

Il punto  $ D(2;4) $ diventa $ D'(4;12) $

$$ D' (2 \cdot n ; 4 \cdot m ) =  D' (2 \cdot 2 ; 4 \cdot 3 ) = D' (4; 12 ) $$

Dopo la trasformazione i nuovi punti A', B', C', D' formano un rettangolo.

Esempio 2

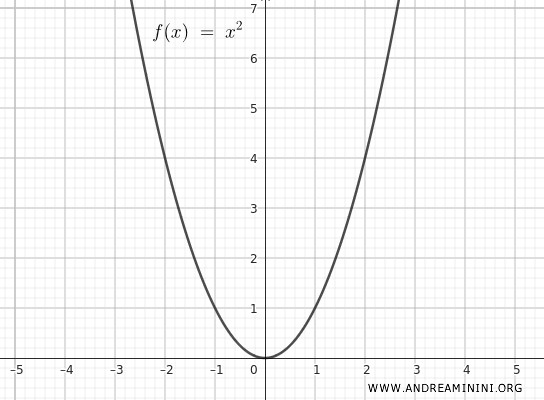
Per comprendere meglio il concetto di dilatazione applicato a una funzione, considero la funzione quadratica \( f(x) = x^2 \).

$$ f(x) = x^2 $$

Il grafico iniziale della funzione è il seguente:

 

Vediamo le possibili dilatazioni/contrazioni della funzione.

Dilatazione/contrazione verticale

Per ottenere una dilatazione o una contrazione verticale, moltiplico l'intera funzione per un fattore \( n \).

Se \( n > 1 \), la funzione si espande verticalmente; se \( 0 < n < 1 \), la funzione si contrae verticalmente.

$$ y = n \cdot f(x) = n \cdot x^2 $$

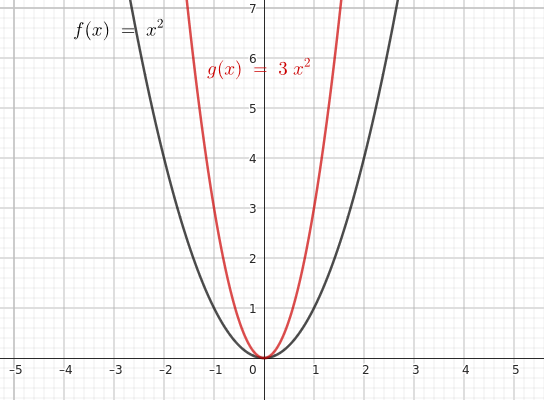
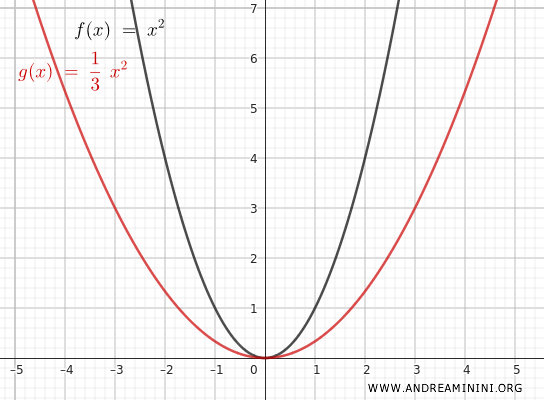
Ad esempio, per $ n = 3 $ la funzione diventa

$$ y = 3x^2 $$

Questa trasformazione triplica ogni valore di \( f(x) \).

Se invece applico $ n = \frac{1}{3} $ la funzione diventa:

$$ y = \frac{1}{3} \cdot x^2 $$

In questo caso la funzione si contrae verticalmente.

Dilatazione/contrazione orizzontale

Per una dilatazione o una contrazione orizzontale, sostituisco \( x \) con \( \frac{x}{m} \) nella funzione.

Se \( m > 1 \), la funzione si allarga orizzontalmente, mentre se \( 0 < m < 1 \), la funzione si restringe orizzontalmente.

$$  y = f\left(\frac{x}{m}\right) = \left(\frac{x}{m}\right)^2 $$

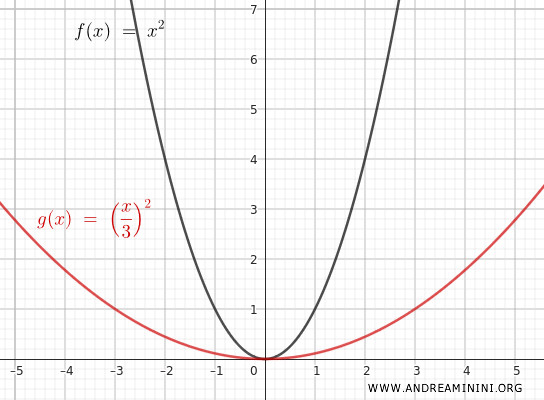
Ad esempio, se \( m = 3 \) la funzione diventa:

$$  y = \left(\frac{x}{3}\right)^2 = \frac{x^2}{9} $$

Questa trasformazione allarga la parabola lungo l'asse x.

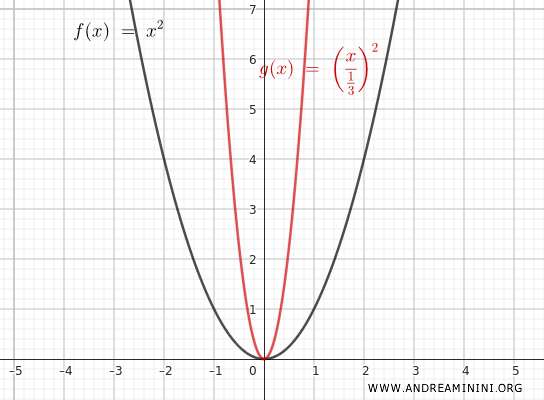
Se invece applico $ m = \frac{1}{3} $ la funzione diventa:

$$  y = \left(\frac{x}{ \frac{1}{3} }\right)^2 = \frac{x^2}{\frac{1}{9}} = 9x^2 $$

In questo caso la funzione si contrae orizzontalmente.

Dilatazione o contrazione combinata

Posso anche combinare entrambe le dilatazioni o contrazioni.

In questo caso la funzione generale dilatata diventa:

$$ y = n \cdot f\left(\frac{x}{m}\right) = n \cdot \left(\frac{x}{m}\right)^2 $$

Ad esempio, per  \( n = 3 \) e \( m = 2 \) ottengo la funzione trasformata in questo modo:

$$ y = 3 \cdot \left(\frac{x}{2}\right)^2 = 3 \cdot \frac{x^2}{4} = \frac{3x^2}{4} $$

Questa trasformazione espande verticalmente la funzione di un fattore 3 e la allarga orizzontalmente di un fattore 2.

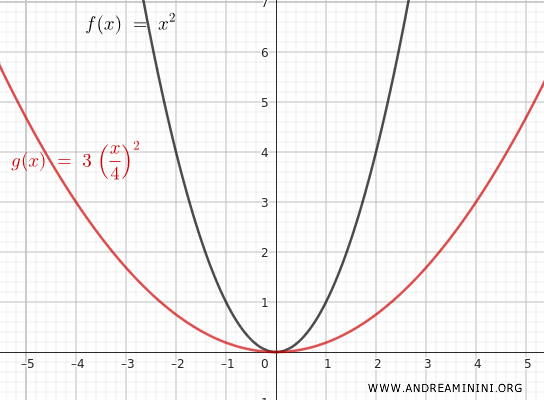
Ad esempio per \( x = 2 \), \( f(x) = 2^2 = 4 \) diventa \( y = \frac{3 \cdot 4}{4} = 3 \). Per \( x = 4 \), \( f(x) = 4^2 = 16 \) diventa \( y = \frac{3 \cdot 16}{4} = 12 \).

In conclusione, nell'esempio della funzione quadratica \( f(x) = x^2 \), la dilatazione verticale e orizzontale influisce sulla dimensione e sulla forma della parabola.

Note

Alcune note a margine e osservazioni personali

• Le dilatazioni come trasformazioni affini
  Una dilatazione rientra tra le trasformazioni affini poiché i suoi coefficienti di scala, \( m \) e \( n \), sono entrambi non nulli (cioè \( m \ne 0 \) e \( n \ne 0 \)). La trasformazione si esprime nel seguente modo: $$ \begin{cases} x' = m x + p \\[4pt] y' = n y + q \end{cases} $$ In questa formulazione il valore di \( m \) regola l’allungamento o la contrazione lungo l’asse \( x \), mentre \( n \) svolge lo stesso ruolo lungo l’asse \( y \). I due coefficienti funzionano quindi come rapporti di scala direzionali.

  Osservazione. Il fatto che \( m \) e \( n \) siano entrambi diversi da zero implica che il determinante della matrice lineare associata è non nullo, perciò la trasformazione è un’affinità a tutti gli effetti: $$ \begin{vmatrix} m & 0 \\ 0 & n \end{vmatrix} = mn \ne 0 $$

E così via.