Dominio del tempo e delle frequenze

Tradizionalmente i segnali vengono studiati nel dominio del tempo e rappresentati da una funzione \( x(t) \), che varia in base alla variabile continua \( t \) (tempo). Tuttavia, c'è un modo alternativo di analizzarli nel dominio della frequenza. In quest'altro caso il segnale è rappresentato da una funzione \( X(f) \) che varia in base alle frequenze.

Entrambi i domini offrono informazioni complementari: il dominio del tempo mostra il comportamento temporale del segnale, mentre il dominio delle frequenze rivela la sua composizione in frequenze.

Si adotta una convenzione per distinguere facilmente tra i due domini:

• \( x(t) \) indica il segnale nel dominio del tempo (lettera minuscola).
• \( X(f) \) indica il segnale nel dominio della frequenza (lettera maiuscola). 

Nel dominio del tempo, la variabile è il tempo \( t \), mentre nel dominio della frequenza la variabile è la frequenza \( f \).

Nota. L'analisi nel dominio della frequenza è molto importante, poiché i segnali nelle telecomunicazioni sono spesso modulati e trasmessi su frequenze specifiche. Comprendere come un segnale si comporta in frequenza permette di ottimizzare la trasmissione, la ricezione e la qualità dei dati trasmessi.

Qual è la differenza tra il dominio del tempo e delle frequenze?

La differenza risiede nel modo in cui il segnale viene rappresentato e studiato.

• Dominio del tempo
  Nel dominio del tempo, si studia il comportamento del segnale nel corso del tempo.  Un segnale è rappresentato come una funzione della variabile tempo (\( t \)). Quindi, si osserva come il segnale varia nel tempo, analizzando i suoi valori istantanei. Questo tipo di analisi è utile per capire l'andamento temporale del segnale, la sua forma d'onda, la durata, i picchi o eventuali discontinuità.

  Esempio: un segnale \( x(t) \) può essere visualizzato come un'onda che si evolve con il passare del tempo.

• Dominio delle frequenze
  Nel dominio delle frequenze, il segnale viene analizzato scomponendolo in componenti sinusoidali di diverse frequenze, per comprenderne il contenuto spettrale. Questa trasformazione avviene tramite la trasformata di Fourier, che converte un segnale \( x(t) \) dal dominio del tempo al dominio delle frequenze, producendo lo spettro \( X(f) \), dove \( f \) rappresenta la frequenza.$$ X(f) = \int_{-\infty}^{+\infty} x(t) e^{-j 2 \pi f t} dt $$ In questo dominio, posso analizzare come l'energia o la potenza del segnale si distribuisce tra le frequenze. Questo permette di identificare le componenti periodiche, armoniche e altre caratteristiche del contenuto spettrale. Pertanto, non tutti i segnali sono trasformabili nel dominio delle frequenze, ma solo quelli chiamati segnali di energia.

  Esempio: la rappresentazione \( X(f) \) indica la distribuzione dell'ampiezza (o energia) del segnale su diverse frequenze, evidenziando quali frequenze sono dominanti.

La trasformata e l'anti-trasformata di Fourier

La trasformata di Fourier e la sua inversa sono strumenti centrali per l'analisi dei segnali nei sistemi di telecomunicazione, perché consentono di passare dal dominio del tempo a quello della frequenza, e viceversa.

La trasformata di Fourier di un segnale \(x(t)\), definito nel dominio del tempo, si calcola tramite la seguente formula: $$ X(f) = \int_{-\infty}^{+\infty} x(t) e^{-j 2 \pi f t} dt $$

Questa equazione trasforma un segnale nel tempo \(x(t)\) nel suo corrispondente spettro \(X(f)\), rappresenta come l'energia del segnale è distribuita tra le varie frequenze.

In particolar modo, mi permette di decomporre un segnale in componenti sinusoidali di diverse frequenze, perché un esponenziale complesso del tipo \( e^{j\alpha} \) posso riscriverlo come combinazione lineare di seni e coseni tramite le formule di Eulero:

$$ e^{j\alpha} = \cos(\alpha) + j\sin(\alpha) $$

In questa rappresentazione trigonometrica dei numeri complessi, la parte reale è il coseno e la parte immaginaria è il seno.

Va detto che solo alcuni segnali sono trasformabili nel dominio delle frequenze tramite la trasformata di Fourier, i segnali di energia che hanno un energia finita $ E_x $, e sono detti segnali Fourier trasformabili.

Nota. L'esponenziale complesso \(e^{-j 2 \pi f t}\) è il nucleo dell'operazione di trasformazione, e agisce come un filtro che separa le componenti frequenziali del segnale. Da notare che l'esponenziale complesso ha segno opposto nella trasformata rispetto alla sua inversa.

L'inversa della trasformata di Fourier (o anti-trasformata) mi permette di ricostruire il segnale nel dominio del tempo partendo dallo spettro di frequenza \(X(f)\). La formula per l'inversa è:

$$ x(t) = \int_{-\infty}^{+\infty} X(f) e^{j 2 \pi f t} df $$

In questo caso l'integrazione avviene sullo spettro \(X(f)\) e, tramite l'esponenziale complesso \(e^{j 2 \pi f t}\), ricostruisco il segnale nel dominio del tempo.

Nota. Queste due formule sono duali: nella prima integro sul tempo per ottenere una funzione della frequenza, mentre nella seconda integro sulla frequenza per ottenere una funzione del tempo. 

A cosa serve la trasformata e l'antitrasformata di Fourier?

Rappresentano la base di tutta l'analisi in frequenza.

Mi permettono di analizzare il comportamento dei sistemi di TLC sia nel dominio del tempo sia in quello della frequenza, ottimizzando così le tecniche di trasmissione e ricezione.

Quindi, sono strumenti essenziali per risolvere esercizi ed esaminare le caratteristiche fisiche dei segnali nei sistemi di telecomunicazione.

Nota. Anche se in alcuni casi è possibile risolvere direttamente l'integrale per ottenere la trasformata o l'inversa, spesso si fa uso delle proprietà delle trasformate (come linearità, traslazione nel tempo o nella frequenza) per evitare calcoli complessi e semplificare l'analisi.

La dualità tra tempo e frequenza

La dualità tra tempo e frequenza è un concetto fondamentale nelle telecomunicazioni.

Descrive la stretta relazione tra la rappresentazione di un segnale nel dominio del tempo (come varia nel tempo) e nel dominio della frequenza (come le componenti frequenziali sono distribuite).

La dualità tra tempo e frequenza è espressa dalla seguente proprietà fondamentale: un segnale concentrato nel tempo ha una rappresentazione larga in frequenza, mentre un segnale esteso nel tempo ha una rappresentazione stretta in frequenza.

Più un segnale è breve nel tempo (ad esempio un impulso), più la sua rappresentazione in frequenza si estende su un'ampia gamma di frequenze.

Viceversa, un segnale lungo nel tempo avrà una rappresentazione in frequenza concentrata attorno a una o poche frequenze.

In telecomunicazioni, questa proprietà è sfruttata per modulare e demodulare i segnali, ottimizzando la larghezza di banda e la potenza di trasmissione.

Nota. La dualità tra tempo e frequenza è garantita dalla trasformata di Fourier, l'operazione che permette di passare dalla rappresentazione nel tempo a quella in frequenza. Se un segnale x(t) nel dominio del tempo è noto, la sua trasformata X(f) fornisce una descrizione di come l'energia del segnale è distribuita sulle varie frequenze. Questa trasformata è bidirezionale: è possibile ricostruire il segnale nel tempo a partire dalla sua rappresentazione in frequenza.

Esempio

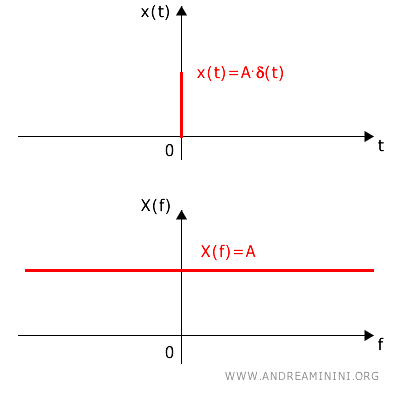
Un esempio estremo di questa dualità è il segnale impulsivo nel tempo, rappresentato da un impulso di Dirac.

La sua trasformata di Fourier è una costante su tutte le frequenze, mostrando che un impulso temporale contiene tutte le frequenze in egual misura.

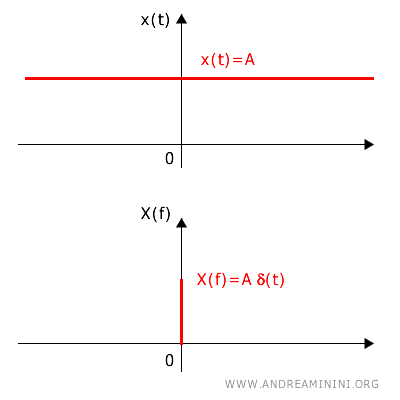
Al contrario, un segnale costante nel tempo avrà una rappresentazione in frequenza come un singolo impulso (delta di Dirac), concentrato in una frequenza specifica.

E così via.