Il segnale rettangolare ( Rect )

Il segnale rettangolare (funzione rettangolare) è un impulso rettangolare di ampiezza costante $ A $ in un intervallo finito di tempo $ T $ e zero altrove.

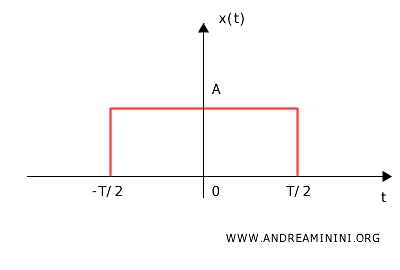
E' anche conosciuto come segnale "Rect" dall'abbreviazione di rectangular pulse.

Si tratta di una funzione matematica usata comunemente in elaborazione dei segnali, telecomunicazioni e teoria dei sistemi.

Nella notazione usata nelle telecomunicazioni la funzione rettangolare di durata $ T $ e ampiezza $ A $ è definita in questo modo:

$$ x(t) = A \cdot \text{Rect}_T(t-τ) $$

Dove $ t $ è la variabile tempo, $ \tau $ è il punto in cui il segnale è centrato, mentre la funzione Rect_T(t) è la seguente:

$$
\text{Rect}_T(t - \tau ) =
\begin{cases}
1 & \text{se } -\frac{1}{2} \cdot T \leq t - \tau \leq \frac{1}{2} \cdot T, \\ \\
0 & \text{altrimenti}.
\end{cases} $$

Quindi, il segnale x(t) di durata $ T $ vale $ A $ all'interno di un intervallo centrato attorno a $ \tau $,  tra \(\tau-\frac{1}{2} T \) e \( \tau + \frac{1}{2} T \).

Al di fuori di questo intervallo vale zero.

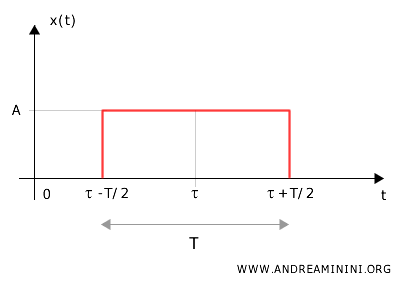
La rappresentazione compatta attraverso la funzione rect rende semplice l'analisi.

Il segnale rect viene usato in sistemi digitali per rappresentare l'inizio e la fine di segnali discreti, nella modulazione d'impulsi e nella codifica di segnali a banda limitata. E' un modello ideale per rappresentare informazioni digitali,

Ad esempio, ogni bit (0 o 1) viene modellato come un segnale rettangolare, dove un bit pari a 1 è rappresentato da un segnale di ampiezza 1, e un bit pari a 0 è rappresentato da un segnale di ampiezza 0.

Nota. Come vedremo con la trasformata di Fourier, nel dominio delle frequenze la trasmissione dei segnali rettangolari richiede l'uso di larghezze di banda molto ampie. Questo implica delle distorsioni nei sistemi reali a causa delle limitazioni del canale trasmissivo, che devono essere gestite con tecniche di modulazione e filtraggio appropriate. Inoltre, il segnale rect è un segnale ideale perché presenta due discontinuità ai bordi. All'inizio il segnale passa da 0 a A istantaneamente. Lo stesso accade alla fine, il segnale salta da A a 0 senza alcuna continuità, il che non è possibile nei sistemi fisici.

Trasformata di Fourier

La trasformata di Fourier di un segnale rettangolare x(t) centrato in t=0 di durata T e di ampiezza A è il prodotto dell'ampiezza e la durata (AT) per la funzione seno cardinale (sinc) $$  x(t) = A \cdot \text{rect}_T(t)   \stackrel{F}{ \Rightarrow } X(f) = AT \cdot \text{Sinc}(f) $$

La funzione Rect è una funzione Fourier-trasformabile perché è un segnale limitato nel tempo, qiundi è segnale di energia che veicola una quantità di energia finita.

Quindi nel dominio delle frequenze il segnale Rect può essere scritto:

$$  X(f) = AT \cdot \text{Sinc}(f) $$

Dove Sinc è il seno cardinale ossia la funzione matematica seguente:

$$ Sinc(f) = \begin{cases} \frac{\sin(πf)}{πf} \:\:\: se \: f \ne 0 \\ \\ 1 \:\:\: se \: f = 0 \end{cases} $$

La funzione Sinc(f) assume il valore 1 in f=0 e oscilla altrove, tendendo a zero quando f tende a più o meno infinito.

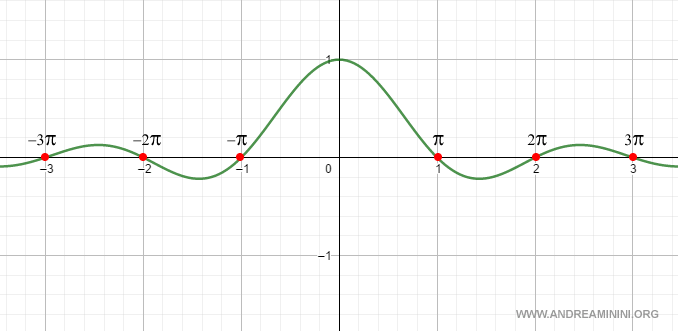
Nota. Si tratta di un segnale ideale definito in una larghezza di banda infinita perché è presente in tutte le frequenze, anche se la maggior parte dell'energia del segnale è concentrata attorno a frequenze basse, vicino a f=0. Quindi, è inevitabile che ci sia una distorsione quando viene trasmesso, perché sarebbe necessario disporre di un canale con larghezza di banda infinita, cosa impossibile da ottenere con i mezzi trasmissivi reali. Inoltre, i segnali con larghezza di banda elevata occupano più spettro e possono interferire con altri segnali. Pertanto, una larghezza di banda teoricamente infinita rappresenta un limite pratico per la trasmissione.

Osservando il risultato della trasformata di Fourier del segnale rettangolare noto che, sebbene il segnale sia limitato nel tempo, ha componenti di frequenza che si estendono su un intervallo ampio.

Questo è il cosiddetto principio di incertezza: segnali limitati nel tempo hanno uno spettro in frequenza esteso, e viceversa.

In altre parole, un segnale che esiste per un tempo limitato ha molte componenti frequenziali.

Questo significa anche che il segnale rettangolare è caratterizzato da transizioni rapide nel tempo, perché richiede una larghezza di banda ampia, ovvero lavora su molte frequenze, ma ha una durata limita nel tempo.

Relazione tra durata del segnale e larghezza di banda. Un concetto chiave qui è che più breve è la durata del segnale nel tempo, più ampia sarà la sua larghezza di banda in frequenza. Questo è il motivo per cui il segnale rettangolare, che ha una durata limitata nel tempo, ha una larghezza di banda infinita. Al contrario, segnali che durano più a lungo nel tempo avranno una larghezza di banda più stretta.

Le trasformate dei segnali ritardati o anticipati nel tempo

Per calcolare la trasformata di Fourier di un segnale z(t) ritardato (causale) o anticipato (anticausale) nel tempo, basta moltiplicare la trasformata dello stesso segnale centrato in zero per un esponenziale complesso.

• Segnale ritardato
  Se il segnale è ritardato nel tempo z(t)=x(t-τ), la sua trasformata di Fourier è uguale alla trasformata X(f) dello stesso segnale x(t) centrato in t=0 (in assenza di ritardo) per un esponenziale complesso di segno negativo e di peso pari al ritardo τ.

  $$  z(t) = A \cdot \text{rect}_T(t-τ)   \stackrel{F}{ \Rightarrow } z(f) = X(f) \cdot e^{-j2 \pi f \tau} $$

• Segnale anticipato
  Se il segnale è anticipato nel tempo z(t)=x(t+τ), la sua trasformata di Fourier è uguale alla trasformata X(f) dello stesso segnale x(t) centrato in t=0 (in assenza di ritardo) per un esponenziale complesso di segno positivo e di peso pari al ritardo τ.

  $$  z(t) = A \cdot \text{rect}_T(t+τ)   \stackrel{F}{ \Rightarrow } z(f) = X(f) \cdot e^{+j2 \pi f \tau} $$

Questo mi permette di calcolare la trasformata di Fourier di qualsiasi segnale rettangolare, sia centrato in zero che ritardato o anticipato nel tempo.

Nota. Il legame tra Rect e Sinc è importante in molti ambiti, nelle telecomunicazione e nell'elaborazione dei segnali, come nella modulazione e nel filtraggio.

Dimostrazione

Per dimostrare le trasformate di Fourier distinguo i tre casi possibili di segnale nel dominio del tempo: centrato in zero, ritardato o anticipato.

A] Segnale x(t) centrato in zero

Il segnale rettangolare è un segnale di enrgia Fourier-trasformabile perché veicola una quantità di enegia finita.

Il segnale \(x(t)\) è costante nell'intervallo \([-T/2, T/2]\), quindi è limitato nel tempo, e ha ampiezza \(A\).

Per verificare che sia un segnale di energia, si calcola l'energia come l'integrale del modulo quadro del segnale.

$$ E = \int_{-T/2}^{T/2} | x(t) |^2 dt T $$

In questo caso è $ x(t)=A $

$$ E = \int_{-T/2}^{T/2} |A|^2 dt  $$

La costante $ A $ può uscire dall'integrale

$$ E = A^2 \cdot \int_{-T/2}^{T/2} \ dt  $$

Risolvo l'integrale ∫ dt = t nell'intervallo (-T/2,T/2)

$$ E = A^2 \cdot \left[ t  \right]_{-T/2}^{T/2}  $$

$$ E = A^2 \cdot \left[ T/2 - (-T/2)  \right]  $$

$$ E = A^2 \cdot \left[ T/2 + T/2  \right]  $$

$$ E = A^2 \cdot T  $$

Quindi, l'integrale del segnale esiste ed è un numero finito $ E = A^2 T $

Nota. Del resto il segnale forma un rettangolo di base $ T $ e altezza $ A^2 $. L'integrale definito non fa altro che calcolare l'area della figura. In questo caso l'area del rettangolo è il prodotto base per altezza ossia $ T \times A^2 $

Questo dimostra che il segnale è limitato e ha un’energia finita, quindi ammette la trasformata di Fourier.

$$ X(f) = \int_{-\infty}^{+\infty} x(t) \cdot e^{-j 2 \pi f t} dt $$

In questo caso è $ x(t)=A $

$$ X(f) = \int_{-\infty}^{+\infty} A \cdot e^{-j 2 \pi f t} dt $$

La costante A può uscire dall'integrale

$$ X(f) =  A \cdot \int_{-\infty}^{+\infty} e^{-j 2 \pi f t} dt $$

Sapendo che il segnale è definito solo nell'intervallo (-T/2, T/2) ed è nullo altrove, restringo l'intervallo di integrazione

$$ X(f) =  A \cdot \int_{-T/2}^{T/2} e^{-j 2 \pi f t} dt $$

Risolvo l'integrale definito.

La regola generale è che l'integrale indefinito di \( e^{kt} \) rispetto a \( t \) è:

$$ \int e^{kt} \, dt = \frac{e^{kt}}{k} + C $$

Quindi, l'integrale definito nell'intervallo (-T/2, T/2) è:

$$ X(f) =  A \cdot \left[ \frac{ e^{-j 2 \pi f t} }{-j 2 \pi f }   \right]_{-T/2}^{T/2}  $$

$$ X(f) =  A \cdot \left( \frac{ e^{-j 2 \pi f T/2} }{-j 2 \pi f }  - \frac{ e^{-j 2 \pi f (-T/2)} }{-j 2 \pi f }  \right)  $$

$$ X(f) =  A \cdot \left( \frac{ e^{-j \pi f T} }{-j 2 \pi f }  - \frac{ e^{j \pi f T} }{-j 2 \pi f }  \right)  $$

$$ X(f) =  A \cdot \left( \frac{ e^{-j \pi f T} - e^{j \pi f T} }{-j 2 \pi f }   \right)  $$

Moltiplico e divido per -1

$$ X(f) =  A \cdot \left( \frac{ e^{-j \pi f T} - e^{j \pi f T} }{-j 2 \pi f }  \cdot \frac{(-1)}{(-1)}  \right)  $$

$$ X(f) =  A \cdot \left( \frac{ e^{j \pi f T} - e^{-j \pi f T} }{j 2 \pi f }   \right)  $$

$$ X(f) =  A \cdot \left( \frac{ e^{j \pi f T} - e^{-j \pi f T} }{j 2 }  \cdot \frac{1}{ \pi f  }  \right)  $$

Applico le formule di Eulero, sapendo che $ \sin α = \frac{e^{jα}-e^{-jα}}{2j} $ con $ α = \pi f T $.

$$ X(f) =  A \cdot \left( \sin( \pi f T )   \cdot \frac{1}{ \pi f  }  \right)  $$

$$ X(f) =  A \cdot \left( \frac{ \sin( \pi f T ) }{ \pi f  }  \right)  $$

Moltiplico e divido per T

$$ X(f) =  A \cdot \left(  \frac{ \sin( \pi f T ) }{ \pi f  } \cdot \frac{T}{T}  \right)  $$

$$ X(f) =  A \cdot \frac{ \sin( \pi f T ) }{ \pi f T } \cdot T   $$

Sapendo che il rapporto $ \frac{\sin(πα)}{πα} = \text{sinc}(α) $ è il seno cardinale con $ α = f T $ ottengo la trasformata di Fourier, ossia il segnale nel dominio delle frequenze:

$$ X(f) =  AT  \cdot \text{sinc} ( f T )   $$

Dove il seno cardinale è uguale a 1 quando si annulla, ovvero quando f=0 e $ \frac{ \sin(πfT) }{πfT} $ altrove

$$ \text{sinc} ( f T ) = \begin{cases} 1 \ \ \ se \ \ f= 0 \\ \\ \frac{ \sin(πfT) }{πfT} \ \ \ se \ \ f \ne 0 \end{cases} $$

B] Segnale ritardato nel tempo

Un segnale rettangolare ritardato nel tempo (segnale causale) è espresso in questa forma

$$ z(t) = x(t - \tau) $$

Dove $ \tau $ è il centro del segnale che corrisponde al ritardo del segnale nel tempo.

Nel dominio del tempo un segnale ritardato appare traslato verso destra rispetto a un segnale x(t) centrato in zero.

La trasformata di Fourier del segnale ritardato z(t) è la seguente:

$$ Z(f) = \int_{- \infty}^{ \infty } z(t) \cdot e^{-j2 \pi f t} \ dt $$

Sapendo che $ z(t) = x(t - \tau) $

$$ Z(f) = \int_{- \infty}^{ \infty } x(t - \tau) \cdot e^{-j2 \pi f t} \ dt $$

Introduco una variabile temporanea $ k = t - \tau $

$$ Z(f) = \int_{- \infty}^{ \infty } x(k) \cdot e^{-j2 \pi f t} \ dt $$

Poiché $ k = t - \tau $ deduco che $ t = k + \tau $ e $ dt = dk $

$$ Z(f) = \int_{- \infty}^{ \infty } x(k) \cdot e^{-j2 \pi f (k+\tau)} \ dk $$

$$ Z(f) = \int_{- \infty}^{ \infty } x(k) \cdot e^{-j2 \pi f \tau} \cdot e^{-j2 \pi f k} \ dk $$

Un esponenziale è costante perché non dipende dalla variabile di integrazione k, quindi posso portarlo fuori dall'integrale.

$$ Z(f) = e^{-j2 \pi f \tau} \cdot \int_{- \infty}^{ \infty } x(k) \cdot e^{-j2 \pi f k} \ dk $$

Guardando bene, ora l'integrale è semplicemente la trasformata di Fourier del segnale x(t) centrato in zero, di cui già conosco la trasformata $ X(f) = AT  \cdot \text{sinc} ( f T ) $.

$$ Z(f) = e^{-j2 \pi f \tau} \cdot \underbrace{ \int_{- \infty}^{ \infty } x(k) \cdot e^{-j2 \pi f k} \ dk }_{X(f)} $$

$$ Z(f) = e^{-j2 \pi f \tau} \cdot X(f) $$

Questo dimostra che la trasformata di Fourier di un segnale ritardato nel tempo è uguale alla trasformata di Fourier X(f) dello stesso segnale centrato in zero (t=0), ovvero senza ritardo, per un esponenziale complesso di segno negativo.

$$ Z(f) = X(f) \cdot e^{-j2 \pi f \tau}  $$

C] Segnale anticipato nel tempo

Un segnale rettangolare anticipato nel tempo si scrive in questo modo:

$$ z(t) = x(t + \tau) $$

Dove $ \tau $ è un valore numerico che corrisponde al centro del segnale che corrisponde all'anticipo del segnale nel tempo.

Un segnale anticipato nel tempo appare appare traslato verso sinistra rispetto a un segnale x(t) centrato in zero.

La trasformata di Fourier del segnale anticipato z(t) è la seguente:

$$ Z(f) = \int_{- \infty}^{ \infty } z(t) \cdot e^{-j2 \pi f t} \ dt $$

Sapendo che $ z(t) = x(t + \tau) $

$$ Z(f) = \int_{- \infty}^{ \infty } x(t + \tau) \cdot e^{-j2 \pi f t} \ dt $$

Introduco una variabile temporanea $ k = t + \tau $

$$ Z(f) = \int_{- \infty}^{ \infty } x(k) \cdot e^{-j2 \pi f t} \ dt $$

Poiché $ k = t + \tau $ deduco che $ t = k - \tau $ e $ dt = dk $

$$ Z(f) = \int_{- \infty}^{ \infty } x(k) \cdot e^{-j2 \pi f (k-\tau)} \ dk $$

$$ Z(f) = \int_{- \infty}^{ \infty } x(k) \cdot e^{-j2 \pi f (-\tau)} \cdot e^{-j2 \pi f k} \ dk $$

$$ Z(f) = \int_{- \infty}^{ \infty } x(k) \cdot e^{j2 \pi f \tau} \cdot e^{-j2 \pi f k} \ dk $$

Anche in questo caso un esponenziale complesso è costante perché non dipende dalla variabile di integrazione k, quindi lo sposto fuori dall'integrale.

$$ Z(f) = e^{j2 \pi f \tau} \cdot \int_{- \infty}^{ \infty } x(k) \cdot e^{-j2 \pi f k} \ dk $$

L'integrale è la trasformata di Fourier dello stesso segnale ma centrato in zero ossia di x(t), di cui già so che la trasformata è $ X(f) = AT  \cdot \text{sinc} ( f T ) $

$$ Z(f) = e^{j2 \pi f \tau} \cdot \underbrace{ \int_{- \infty}^{ \infty } x(k) \cdot e^{-j2 \pi f k} \ dk }_{X(f) } $$

$$ Z(f) = e^{j2 \pi f \tau} \cdot X(f) $$

Questo dimostra che la trasformata di Fourier di un segnale anticipato nel tempo è uguale alla trasformata di Fourier X(f) dello stesso segnale centrato in zero (t=0), ovvero senza anticipo, per un esponenziale complesso di segno positivo.

$$ Z(f) = X(f) \cdot e^{j2 \pi f \tau}  $$

Nota. In un segnale anticipato l'esponenziale complesso ha segno positivo mentre in un segnale ritardato ha segno negativo. E' importante non confondersi.

E così via.