I segnali ritardati e anticipati

Quando un segnale viene ritardato o anticipato, viene semplicemente spostato lungo l'asse dei tempi senza modificare la sua forma.

Questa traslazione temporale può essere espressa matematicamente come:

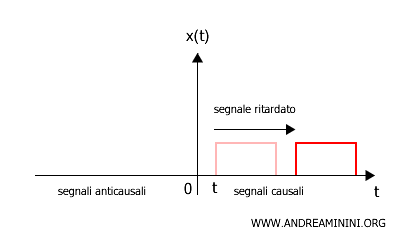
• Segnale ritardato
  Un segnale ritardato di \( \tau \) è rappresentato da \( z(t) = x(t - \tau) \), dove il segnale \( x(t) \) viene spostato verso i tempi futuri. Questo significa che il segnale non inizia a essere trasmesso immediatamente, ma viene posticipato di \( \tau \) secondi. Si verifica una traslazione verso destra sull'asse del tempo.
  
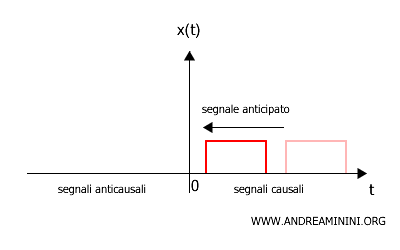
• Segnale anticipato
  Un segnale anticipato di \( \tau \) è rappresentato da \( y(t) = x(t + \tau) \), dove il segnale \( x(t) \) viene spostato verso i tempi passati. In questo caso, il segnale si verifica prima nel tempo rispetto al segnale di riferimento. In questo caso si verifica una traslazione verso sinistra sull'asse del tempo.
  

Sebbene matematicamente sia possibile anticipare un segnale, nella pratica esistono dei limiti fisici.

I segnali trasmessi nei sistemi di telecomunicazione reali sono sempre segnali causali, il che significa che non possono reagire a segnali futuri.

In alcuni casi un segnale anticipato potrebbe anche diventare non causale, e quindi non realizzabile in molti sistemi fisici.

Ad esempio, un segnale anticipato potrebbe risultare non causale (anticausale) se viene traslato in istanti di tempo negativi (t<0), ovvero nel passato, e quindi non realizzabile fisicamente.

Pertanto, l'anticipazione del segnale è un'operazione teorica che potrebbe non essere realizzabile in tutti i casi.

La trasformata di Fourier dei segnali ritardati o anticipati

Vale la pena sottolineare che, in questo caso, nell'esponenziale complesso c'è il ritardo/anticipo $ \tau $, non c'è la variabile tempo $ t $.

La dimostrazione

La trasformata di Fourier di un segnale generico \( x(t) \) è definita come:

$$ X(f) = \int_{-\infty}^{+\infty} x(t) e^{-j 2 \pi f t} dt $$

Considero il segnale ritardato \( z(t) = x(t - \tau) \), la sua trasformata di Fourier è la seguente:

$$ Z(f) = \int_{-\infty}^{+\infty} z(t) e^{-j 2 \pi f t} dt $$

$$ Z(f) = \int_{-\infty}^{+\infty} x(t - \tau) e^{-j 2 \pi f t} dt $$

Introduco un cambio di variabile ponendo \( k = t - \tau \) e notando che \( dk = dt \)

Poi riscrivo l'integrale in termini della nuova variabile \( k \):

$$ Z(f) = \int_{-\infty}^{+\infty} x(k) e^{-j 2 \pi f (k + \tau)} dk $$

$$ Z(f) = \int_{-\infty}^{+\infty} x(k) e^{-j 2 \pi f k} \cdot e^{-j 2 \pi f \tau} dk $$

Il secondo esponenziale esce dall'integrale perché è una costante, in quanto è indipendente dalla variabile di integrazione k.

$$ Z(f) = \left( \int_{-\infty}^{+\infty} x(k) e^{-j 2 \pi f k} dk \right) \cdot e^{-j 2 \pi f \tau} $$

L'espressione tra parentesi è la trasformata di Fourier originale \( X(f) \) del segnale $ x(t) $ senza traslazione.

$$ Z(f) =  \underbrace{ \left( \int_{-\infty}^{+\infty} x(k) e^{-j 2 \pi f k} dk \right) }_{X(f)} \cdot e^{-j 2 \pi f \tau} $$

$$ Z(f) = X(f) \cdot e^{-j 2 \pi f \tau} $$

Questo mostra che la trasformata di Fourier del segnale ritardato è uguale alla trasformata del segnale originale moltiplicata per un fattore esponenziale complesso \( e^{-j 2 \pi f \tau} \), che introduce una rotazione di fase nel dominio della frequenza.

Se il segnale è anticipato seguo la stessa procedura,ma l'esponenziale complesso diventa positivo \( e^{j 2 \pi f \tau} \).

$$ Y(f) = X(f) \cdot e^{j 2 \pi f \tau} $$

Nota. Questa proprietà di traslazione mi permette di calcolare rapidamente la trasformata di Fourier di segnali spostati nel tempo senza dover rifare tutto l'integrale. Mi basta conoscere la trasformata del segnale non traslato e moltiplicare per il fattore esponenziale appropriato.

Dimostrazione del segnale anticipato

Se considero il segnale anticipato \( y(t) = x(t + \tau) \) nel tempo, la sua trasformata di Fourier è:

$$ Y(f) = \int_{-\infty}^{+\infty} y(t) e^{-j 2 \pi f t} dt $$

$$ Y(f) = \int_{-\infty}^{+\infty} x(t + \tau) e^{-j 2 \pi f t} dt $$

Anche in questo caso introduco un cambio di variabile ponendo \( k = t + \tau \) con \( dk = dt \)

Poi riscrivo l'integrale sostituendo $ t = k-\tau $ e $ dt = dk $.

$$ Y(f) = \int_{-\infty}^{+\infty} x(k) e^{-j 2 \pi f (k - \tau)} dk $$

Applico le proprietà degli esponenziali e semplifico.

$$ Y(f) = \int_{-\infty}^{+\infty} x(k) e^{-j 2 \pi f k} \cdot e^{-j 2 \pi f (- \tau)} dk $$

$$ Y(f) = \int_{-\infty}^{+\infty} x(k) e^{-j 2 \pi f k} \cdot e^{j 2 \pi f  \tau} dk $$

Il secondo esponenziale esce dall'integrale perché è una costante.

$$ Y(f) = \left( \int_{-\infty}^{+\infty} x(k) e^{-j 2 \pi f k} dk \right) \cdot e^{j 2 \pi f \tau} $$

L'espressione tra parentesi è la trasformata di Fourier originale \( X(f) \).

$$ Y(f) =  \underbrace{ \left( \int_{-\infty}^{+\infty} x(k) e^{-j 2 \pi f k} dk \right) }_{X(f)} \cdot e^{j 2 \pi f \tau} $$

$$ Y(f) = X(f) \cdot e^{j 2 \pi f \tau} $$

Quindi, nel caso di un segnale anticipato l'unica differenza è l'esponente positivo dell'esponenziale complesso. 

Un esempio pratico

Supponiamo di avere un segnale rettangolare nel tempo, centrato in zero, con una durata \( T \) e ampiezza \( A \).

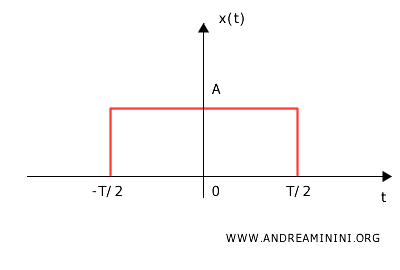
La sua trasformata di Fourier è una funzione sinc (seno cardinale):

$$ X(f) = A T \cdot \text{sinc}(f T) $$

Se questo segnale viene ritardato di \( \tau \), la nuova trasformata diventa:

$$ Z(f) = X(f) \cdot e^{-j 2 \pi f \tau} $$

$$ Z(f) = A T \cdot \text{sinc}(f T) \cdot e^{-j 2 \pi f \tau} $$

Viceversa, se viene anticipato di \( \tau \), la nuova trasformata diventa:

$$ Y(f) = X(f) \cdot e^{j 2 \pi f \tau} $$

$$ Y(f) = A T \cdot \text{sinc}(f T) \cdot e^{j 2 \pi f \tau} $$

In conclusione, la trasformata di Fourier di un segnale traslato (ritardato o anticipato) si ottiene moltiplicando la trasformata del segnale originale per un esponenziale complesso che dipende dalla quantità di ritardo o anticipo.

E così via.