La trasformata di Fourier
La trasformata di Fourier mi permette di scomporre una funzione non periodica in una combinazione lineare di funzioni con base ejwt dove ω di R. $$ F(ω) = \int_{-\infty}^{+\infty} f(t) \: e^{-jωt} \: dt $$ purché la funzione soddisfi la condizione di assoluta sommabilità.
Il segnale viene scomposto in un integrale, detto integrale di Fourier che può essere scritto in forma esponenziale.
$$ F(ω) = \int_{-\infty}^{+\infty} f(t) \: e^{-jωt} \: dt $$
Dove ω è la frequenza angolare. In alcuni contesti è anche indicata come frequenza ciclica ω=2πf
I coefficienti della combinazione lineare sono i dati della funzione continua F(ω) che rappresenta lo spettro della funzione f(t).
Attenzione. La condizione di assoluta sommabilità è una condizione necessaria per la F-trasformata. Se nella funzione da trasformare manca questa condizione, non si può calcolare la F-trasformata della funzione.
L'anti-trasformata di Fourier
Come già visto per la trasformata di Laplace anche la trasformata di Fourier ha un'anti-trasformata.
$$ f(t) = \frac{1}{2π} \int_{-\infty}^{+\infty} F(ω) \: e^{jωt} \: dω $$
L'anti-trasformata di Fourier determina il segnale f(t) a partire dallo spettro F(ω)
Qual è la differenza tra serie e trasformata di Fourier. La trasformata di Fourier è un caso limite della serie di Fourier. La serie di Fourier mi permette di sviluppare in serie solo le funzioni dei segnali periodici. La trasformata di Fourier, invece, mi consente lo sviluppo in serie anche dei segnali non periodici.
Un esempio pratico
Esempio 1
La funzione del segnale nel tempo è
$$ u(t) = \frac{1}{1+t^2} $$
La trasformata di Fourier della funzione è la seguente
$$ F(ω) = \int_{-\infty}^{+\infty} u(t) \cdot e^{-jωt} \: dt $$
$$ F(ω) = \int_{-\infty}^{+\infty} \frac{1}{1+t^2} \cdot e^{-jωt} \: dt $$
$$ F(ω) = \int_{-\infty}^{+\infty} \frac{e^{-jωt}}{1+t^2} \: dt $$
Esempio 2
Prendo in considerazione un semplice segnale a impulso.
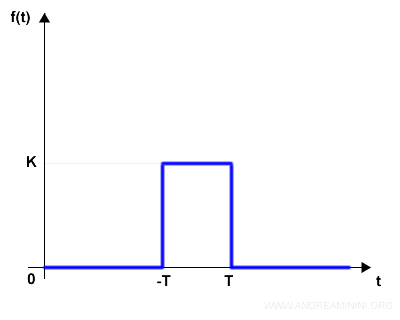
C'è un solo impulso di ampiezza K che si verifica dall'istante -τ all'istante τ, mentre negli altri istanti temporali il segnale è nullo.
La funzione temporale f(t) dell'impulso è
$$ f(t) = \begin{cases} K \:\:\: se \:\: t \in [-τ,τ] \\ \\ 0 \end{cases} $$
Si tratta di un segnale sommabile perché l'area al di sotto della funzione è finita.
La trasformata di Fourier per ω=0 è
$$ F(0) = \int_{-\infty}^{+\infty} f(t) \: dt = \int_{-τ}^τ K \: dt $$
$$ F(0) = K \int_{-τ}^τ \: dt $$
$$ F(0) = K \cdot (τ - (-τ)) $$
$$ F(0) = 2τK $$
Per ω≠0
$$ F(ω) = \int_{-\infty}^{+\infty} e^{-jωt} \: dt $$
$$ F(ω) = K \cdot \int_{-τ}^{τ} e^{-jωt} \: dt $$
$$ F(ω) = K \cdot [ \frac{e^{-jωt}}{-jω} ]_{-τ}^τ $$
$$ F(ω) = \frac{2K}{ω} \sin(ωτ) $$
In questo caso lo spettro della funzione f(t) è reale
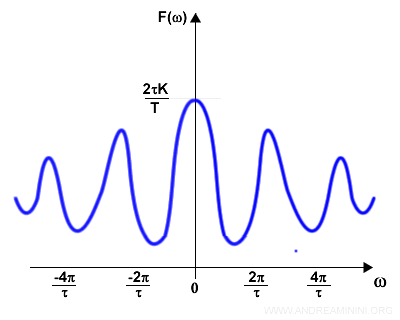
La dimostrazione e spiegazione
Prendo in considerazione un segnale f(t) impulsivo non periodico.
Un segnale impulsivo tende a zero per t tendente a -∞ e +∞.
Questo segnale rispetta il vincolo di sommabilità perché l'area tra il grafico della funzione e l'ascisse è un numero finito.
$$ \int_{-\infty}^{+ \infty} |f(t)| \: dt \le M < \infty $$
Qualsiasi segnale non periodico ( es. un impulso ) posso considerarlo come il caso limite di un segnale periodico in cui il periodo T tende a infinito e la pulsazione fondamentale Ω tende a zero.
Posta la pulsazione uguale a
$$ ω = kΩ $$
l'incremento tra due pulsazioni successive è
$$ Δω = (k+1)Ω-kΩ = Ω $$
Considerando la serie di Fourier in forma esponenziale
$$ f(t) = \sum_{k=\infty}^{+\infty} F_k e^{jkΩt} $$
Sostituisco kΩ con ω
$$ f(t) = \sum_{k=-\infty}^{+\infty} F_k e^{jωt} $$
L'incremento Δω tra due pulsazioni successive nel periodo T è
$$ f(t) = \sum_{ω=-\infty}^{+\infty} F(ω) \frac{Δω}{T} e^{jωt} $$
$$ f(t) = \frac{1}{T} \cdot \sum_{ω= - \infty}^{+\infty} F(ω) \cdot e^{jωt} \cdot Δω $$
Poiché T=2π
$$ f(t) = \frac{1}{2π} \cdot \sum_{ω= - \infty}^{+\infty} F(ω) e^{jωt} \cdot Δω \:dt $$
Se faccio tendere la funzione a infinito, l'incremento Δω della pulsazione tende a zero, diventando un infinitesimo dω.
L'area tra il grafico è l'ascisse è un integrale pari a
$$ f(t) = \frac{1}{2π} \cdot \int_{- \infty}^{+\infty} F(ω) e^{jωt} \:dω $$
Ho ottenuto l'integrale di Fourier in forma esponenziale e da quest'ultimo ricavo la trasformata di Fourier.
$$ F(ω) = \frac{1}{2π} \cdot \int_{- \infty}^{+\infty} f(t) e^{-jωt} \:dt $$
La forma trigonometrica
Se il segnale f(t) è una funzione reale, l'integrale di Fourier si può riscrivere in forma trigonometrica.
$$ f(t) = \frac{1}{π} \int_0^{+\infty} a(ω) \cos(ωt) + b(ω) \sin(ωt) \: dω $$
I coefficienti dello sviluppo a(ω) e b(ω) sono funzioni continue reali
$$ a(ω) = 2 \int_{-\infty}^{+\infty} f(t) \cos(ωt) \: dt $$
$$ b(ω) = 2 \int_{-\infty}^{+\infty} f(t) \sin(ωt) \: dt $$
La trasformata di Fourier in forma trigonometrica è
$$ f(t) = \frac{1}{π} \int_{0}^{+\infty} c(ω) \cos(ωt+Φω) \: dω $$
Dove
$$ c(ω)=\sqrt{a^2(ω)+b^2(ω)} = 2|F(ω)| $$
$$ Φ(ω) = \arctan \frac{-b(ω)}{a(ω)} = \: arg \: F(ω) $$
La differenza tra trasformata di Fourier e Laplace
Metto a confronto la trasformata di Laplace F(s) e di Fourier
La trasformata di Laplace
$$ F(s) = \int_0^{\infty} f(t) e^{-st} \: dt $$
La L-trasformata è costruita su base e-st dove s è un numero complesso. Pertanto, si tratta di una funzione complessa di variabile complessa
$$ F(s):C \rightarrow C $$
Inoltre, la L-trasformata si applica soltanto nei casi in cui la funzione è nulla per t<0.
La trasformata di Fourier
$$ F(ω) = \int_{-\infty}^{+\infty} f(t) \: e^{-jωt} \: dt $$
La F-trasformata è costruita su base e-jωt dove la pulsazione ω è un numero reale ω∈R.
Quindi, è una funzione complessa di variabile reale
$$ F(w):R \rightarrow C $$
Inoltre, la F-trasformata si applica soltanto alle funzioni sommabili mentre la L-trasformata non è vincolata a questa caratteristica.
La trasformata di Fourier nelle telecomunicazioni
Nelle telecomunicazioni la trasformata di Fourier è scritta nella notazione $$ X(f) = \int_{-\infty}^{+\infty} x(t) \cdot e^{-j 2 \pi f t} dt $$ mentre l'anti-trasformata è $$ x(t) = \int_{-\infty}^{+\infty} x(t) \cdot e^{j 2 \pi f t} dt $$ Dove x(t) è un segnale nel tempo mentre X(f) è lo spettro delle frequenze del segnale.
In questa forma, \( f \) rappresenta la frequenza ciclica (misurata in hertz, Hz), cioè il numero di cicli al secondo.
$$ X(f) = \int_{-\infty}^{+\infty} x(t) \cdot e^{-j 2 \pi f t} dt $$
L'espressione \( 2 \pi f \) è utilizzata perché una sinusoide completa un ciclo ogni \( 2 \pi \) radianti, quindi la relazione tra la frequenza ciclica \( f \) e la frequenza angolare è \( \omega = 2 \pi f \).
Nella notazione della trasformata di Fourier usata in fisica, invece, \( \omega \) rappresenta la frequenza angolare misurata in radianti al secondo, rad/s.
$$ X(\omega) = \int_{-\infty}^{+\infty} x(t) \cdot e^{-j \omega t} dt $$
In questo caso, non c'è bisogno del fattore \( 2 \pi \), poiché la frequenza angolare è già espressa in termini di radianti, che sono la misura naturale per il tempo nella descrizione delle onde sinusoidali.
Nota. Entrambe le formule sono corrette, ma utilizzano convenzioni diverse per esprimere la frequenza. La differenza tra le due rappresentazioni della trasformata di Fourier deriva solo dal modo in cui viene trattata la frequenza.
Le due espressioni sono equivalenti, con la semplice relazione:
$$ \omega = 2 \pi f $$
Dove \( f \) è la frequenza ciclica (in hertz), mentre \( \omega \) è la frequenza angolare (in radianti al secondo).
Quando conviene usare l'una rispetto all'altra?
- La forma con \( f \) (frequenza ciclica) è più comune in contesti pratici come telecomunicazioni e ingegneria del segnale, poiché le frequenze in hertz sono più intuitive e direttamente misurabili.
- La forma con \( \omega \) (frequenza angolare) è più comune in contesti matematici e fisici, dove si lavora con equazioni differenziali e modelli teorici, poiché la frequenza angolare semplifica molte espressioni che coinvolgono sinusoidi.
In conclusione, la scelta tra le due notazioni dipende dal contesto ma concettualmente esprimono la stessa trasformazione.
Le proprietà della trasformata di Fourier
La trasformata di Fourier ha delle proprietà simmetriche molto utili che è il caso di ricordare.
- La trasformata di Fourier di un segnale x(t) reale e pari è una funzione X(f) reale pura e pari
In questo caso la trasformata è una funzione pari $ X(f)=X(-F) $ ed è composta solo dalla parte reale. $$ x(t) = x(-t) \in \mathbb{R} \Rightarrow X(f) = X(-f) \in \mathbb{R} $$ - La trasformata di Fourier di un segnale x(t) reale e dispari è una funzione X(f) immaginaria pura e dispari
In questo caso la trasformata è una funzione dispari $ X(f)=-X(-F) $ ed è composta solo dalla parte immaginaria. $$
x(t) = -x(-t) \in \mathbb{R} \Rightarrow X(f) = -X(-f) \in \mathbb{I} $$ - La trasformata di Fourier di un segnale x(t) né reale, né dispari è una funzione X(f) complessa
In questo caso la trasformata è una funzione composta sia dalla parte reale che dalla parte immaginaria. - La dualità di un segnale x(t) e la sua trasformata di Fourier X(t)
Il valore dello spettro X(f) in f=0 corrisponde all'area del segnale nel tempo, e il valore del segnale x(t) in t=0 corrisponde all'area dello spettro in frequenza. $ X(F) $ in frequenza. $$ x(t) |_{t=0} = \int_{-\infty}^{\infty} X(f) \ df $$ $$ X(f) |_{f=0} = \int_{-\infty}^{\infty} x(t) \ dt $$
Queste proprietà sono molto utili per verificare se il risultato della trasformata di Fourier è corretto o meno.
Ad esempio, se ho un segnale x(t) reale e pari nel dominio del tempo e il risultato della trasformata di Fourier è una funzione dispari e/o la funzione ha una parte immaginaria, è subito chiaro che ho commesso qualche errore nel calcolo.
Ecco altre proprietà utili
- La traslazione di un segnale nel tempo
Quando un segnale viene traslato nel tempo (ritardato o anticipato), la sua trasformata di Fourier si modifica introducendo un fattore esponenziale complesso, dove \( \tau \) rappresenta la quantità di ritardo o anticipo.
- Se il segnale è ritardato \( z(t) = x(t - \tau) \), la sua trasformata di Fourier è il prodotto della trasformata del segnale non traslato $ X(f) $ per un esponenziale complesso con esponente negativo $$ Z(f) = X(f) \cdot e^{-j 2 \pi f \tau} $$
- Se il segnale è anticipato \( y(t) = x(t + \tau) \), la sua trasformata di Fourier è il prodotto della trasformata del segnale non traslato $ X(f) $ per un esponenziale complesso con esponente positivo $$ Y(f) = X(f) \cdot e^{j 2 \pi f \tau} $$
- Teorema della modulazione in frequenza
La moltiplicazione di un segnale $ x(t) $ nel dominio del tempo per un esponenziale complesso $ e^{\pm j2 \pi f_0 t} $ comporta una traslazione del suo spettro nel dominio delle frequenze.- Se il segnale \( x(t) \) è moltiplicato per per \( e^{-j 2 \pi f_0 t} \) sposta lo spettro di \( x(t) \) verso le basse frequenze, centrando lo spettro risultante su \( -f_0 \). $$ x(t) \cdot e^{-j2 \pi f_0 t} \stackrel{F}{ \Longrightarrow } X(f+f_0) $$
- Se il segnale \( x(t) \) è moltiplicato per \( e^{j 2 \pi f_0 t} \), lo spettro viene spostato verso le alte frequenze ed è centrato su \( +f_0 \). $$ x(t) \cdot e^{j2 \pi f_0 t} \stackrel{F}{ \Longrightarrow } X(f-f_0) $$
E così via.
