Impulso o segnale impulsivo

Il segnale impulsivo (o segnale delta) una funzione matematica ideale con un impulso di ampiezza infinita concentrato in un singolo punto nel tempo. $$ \delta (t) = \begin{cases} 1 \ \ \ se \ \ t=0 \\ \\ 0 \ \ \ se \ \ t \ne 0 \end{cases}  $$

In altre parole, un impulso può essere immaginato come un segnale di durata nulla e ampiezza infinita.

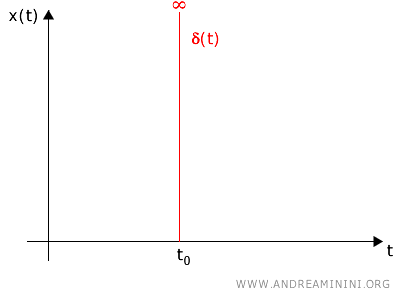
Pur avendo una larghezza infinitesimale e un altezza (ampiezza) infinita, il suo integrale sull’intero asse temporale è pari a 1.

$$ \int_{-\infty}^{\infty} \delta(t) \, dt = 1 $$

In pratica, anche se il segnale delta non può essere realizzato fisicamente, può essere approssimato da impulsi molto stretti e di grande ampiezza.

Spesso il segnale impulsivo è anche chiamato impulso di Dirac o delta di Dirac δ(t).

E' un concetto fondamentale nelle telecomunicazioni e nell'elaborazione dei segnali. E' utilizzato come modello per descrivere segnali molto brevi e intensi. È anche usato nell'elaborazione dei segnali per analizzare la risposta di un sistema a un impulso unitario, chiamata risposta all'impulso del sistema.

Una proprietà fondamentale dell'impulso di Dirac

Per qualsiasi funzione \( g(t) \) centrata in $ t_0 $, l'impulso di Dirac "campiona" la funzione traslata nel tempo nel punto in cui è centrata \( t_0 \).

$$ \int_{-\infty}^{\infty} \delta(t - t_0) \cdot g(t) \, dt = g(t_0) $$

In altre parole, l'integrale dell'impulso di Dirac $ \delta(t - t_0)  $ moltiplicato per g(t)) "campiona" la funzione nel punto t₀​, restituendo il valore $ g(t_0) $.

Nota che se il segnale è centrato in zero nel dominio del tempo $ t_0 = 0 $ l'integrale diventa semplicemente $$ \int_{-\infty}^{\infty} \delta(t) \cdot g(t) \, dt = g(0) $$

La trasformata di Fourier del segnale impulsivo

La trasformata di Fourier dell'impulso di Dirac è una costante nel dominio della frequenza: $$ \mathcal{F} \{\delta(t)\} = \int_{-\infty}^{\infty} \delta(t) e^{-j 2 \pi f t} \, dt = 1 $$

Questo indica che un impulso di Dirac nel dominio del tempo contiene tutte le frequenze in modo uniforme.

In altre parole, ha uno spettro piatto nel dominio della frequenza.

Se l'impulso è traslato nel tempo, ad esempio \( \delta(t - t_0) \), la sua trasformata di Fourier è:

$$ \mathcal{F} \{\delta(t - t_0)\} = e^{-j 2 \pi f t_0} $$

Questa espressione mostra che lo spostamento dell'impulso nel tempo si traduce in un cambiamento di fase nel dominio della frequenza.

Esempio

Considero un segnale impulsivo di ampiezza $ A $ nell'istante $ t=0 $ e nullo altrove.

$$ x(t) = A \cdot \delta (t) $$

La trasformata di Fourier di questo segnale è la seguente:

$$ X(f) = \int_{-\infty}^{\infty} x(t) e^{-j 2 \pi f t} \, dt $$

In questo caso $ x(t) = A \cdot \delta (t) $

$$ X(f) = \int_{-\infty}^{\infty} (A \cdot \delta (t)) \cdot e^{-j 2 \pi f t} \, dt $$

Poiché $ A $ è un valore costante che moltiplica la funzione integranda, può uscire dall'integrale.

$$ X(f) = A \cdot \int_{-\infty}^{\infty}  \delta (t) \cdot e^{-j 2 \pi f t} \, dt $$

Secondo la proprietà fondamentale dell'impulso di Dirac, per qualsiasi funzione \( g(t) \) l'integrale è

$$ \int_{-\infty}^{\infty} \delta(t - t_0) \cdot g(t) \, dt = g(t_0) $$

In questo caso, la funzione \( g(t) = e^{-j 2 \pi f t} \) e la funzione è centrata in $ t_0=0 $. Quindi, $ g(t_0) = e^{-j 2 \pi f \cdot 0} $

$$ X(f) = A \cdot e^{-j 2 \pi f \cdot 0} $$

$$ X(f) = A \cdot e^{0} $$

Poiché $ e^0=1 $

$$ X(f) = A \cdot 1 $$

$$ X(f) = A $$

Questo vuol dire che il segnale costante in frequenza e ha una larghezza di banda infinita.

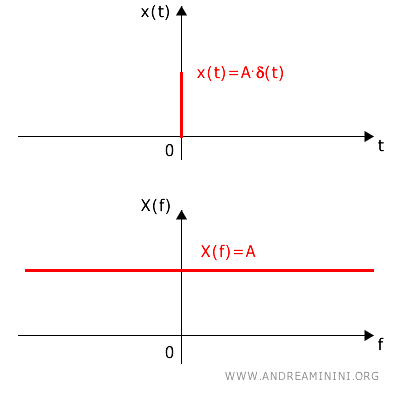
Questo risultato riflette una delle proprietà fondamentali della dualità tra tempo e frequenza. 

Se un segnale nel dominio del tempo è un impulso di Dirac δ(t)), la sua trasformata di Fourier è una costante nel dominio della frequenza, e viceversa.

La dualità tra tempo e frequenza è una delle proprietà fondamentali dell'analisi dei segnali e della trasformata di Fourier. Quando il segnale nel tempo diventa un impulso (cioè è diverso da zero in un unico istante), la sua trasformata di Fourier si estende nel dominio delle frequenze. Inversamente, se la durata del segnale si allunga nel tempo, la sua rappresentazione in frequenza si restringe. Ad esempio, se un segnale nel dominio del tempo è una costante x(t)=A, la sua trasformata di Fourier è un impulso di Dirac nel dominio della frequenza.

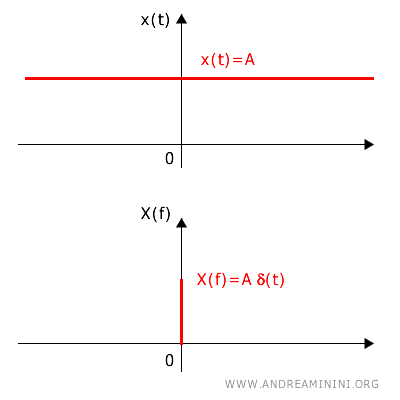
Pertanto, quando un segnale ha la durata minima possibile nel tempo (un impulso), la sua trasformata si espande su tutte le frequenze, da -∞ a +∞. Al contrario, quando un segnale nel tempo è una costante, la sua trasformata è un impulso in frequenza.

La trasformata di Fourier del segnale impulsivo traslato nel tempo

Questo segue dalla proprietà generale della trasformata di Fourier per un segnale traslato nel tempo \( x(t \pm \tau) \). 

Quindi, non occorre calcolare di nuovo l'integrale della trasformata di Fourier.

Basta ricordarsi che la trasformata di qualsiasi segnale traslato nel tempo $ x(t \pm \tau) $ si ottiene moltiplicando la trasformata X(f) del segnale centrato in $ t=0 $ per un esponenziale complesso negativo $ e^{-2j \pi f \tau}  $ nel caso di un ritardo, o positivo $ e^{2j \pi f \tau}  $ nel caso di un anticipo.

$$ x(t \pm \tau) \stackrel{F}{\Rightarrow} X(f) \cdot e^{\mp 2j \pi f \tau} $$

Nota. Per qualsiasi segnale traslato nel tempo, la trasformata di Fourier introduce un fattore di esponenziale complesso che tiene conto della direzione e dell'entità della traslazione temporale.

Esempio

Considero un segnale impulsivo ritardato nel tempo

$$ x(t) = A \cdot \delta( t - \tau ) $$

Questo segnale ha un'ampieazza $ A $ ed è centrato nell'istante $ \tau $ ovvero quello che annulla l'argomento $ (t - \tau ) $.

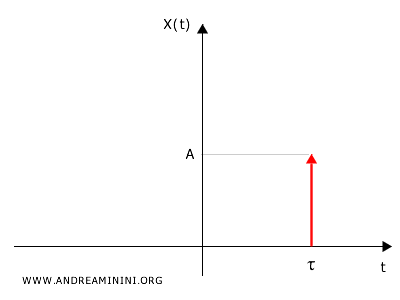
In questo caso il segnale $ x(t) $ è il prodotto tra una costante $ A $ e un delta di dirac ritardato $ \delta(t-\tau) $.

• La costante $ A $ rimane immutata perché è indipendente dal tempo e può uscire dall'integrale.
• La trasformata del delta di dirac in $ t=0 $ è $$ \delta(t) \stackrel{F}{\Rightarrow} 1 $$ Quindi, la trasformata del segnale ritardato è $$   \delta(t - \tau ) \stackrel{F}{\Rightarrow} 1 \cdot e^{-2j \pi f \tau} $$

Questo significa che la trasformata del segnale ritardato nel tempo è:

$$ x(t) = A \cdot \delta( t - \tau ) \stackrel{F}{\Rightarrow} A \cdot 1 \cdot e^{-2j \pi f \tau} $$

Quindi, la trasformata di Fourier del segnale è la seguente:

$$ X(f) = A \cdot e^{-2j \pi f \tau}  $$

Esempio 2

Considero un segnale impulsivo anticipato nel tempo

$$ x(t) = A \cdot \delta( t + \tau ) $$

Il segnale ha ancora un'ampieazza $ A $ ma è centrato nell'istante $ - \tau $.

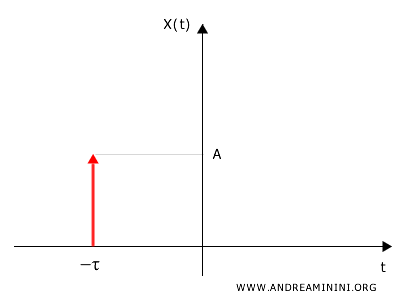
In questo caso il segnale $ x(t) $ è il prodotto tra una costante $ A $ e un delta di dirac anticipato $ \delta(t + \tau) $.

• La costante $ A $ rimane invariata perché è indipendente dal tempo..
• La trasformata del delta di dirac in $ t=0 $ è $$ \delta(t) \stackrel{F}{\Rightarrow} 1 $$ Quindi, la trasformata del segnale anticipato è $$ \delta(t + \tau ) \stackrel{F}{\Rightarrow} 1 \cdot e^{2j \pi f \tau} $$

Pertanto, la trasformata del segnale anticipato nel tempo è:

$$ x(t) = A \cdot \delta( t + \tau ) \stackrel{F}{\Rightarrow} A \cdot 1 \cdot e^{2j \pi f \tau} $$

Quindi, la trasformata di Fourier del segnale è la seguente:

$$ X(f) = A \cdot e^{2j \pi f \tau}  $$

E così via