Il fasore

Un fasore è la rappresentazione grafica o matematica di un segnale sinusoidale sul piano di Gauss.

E' un concetto utilizzato nell'analisi dei segnali elettrici in relazione ai fenomeni alternati come le correnti e le tensioni alternate.

In altre parole, un fasore è una rappresentazione di una grandezza sinusoidale, come la tensione o la corrente, che varia nel tempo.

A cosa serve? I fasori sono utilizzati per semplificare l'analisi di circuiti in corrente alternata (AC), perché mi permettono di evitare l'utilizzo delle equazioni differenziali che descrivono le variazioni nel tempo di tensione e corrente, sostituendole con equazioni algebriche più semplici. In sostanza, l'uso dei fasori mi consente di analizzare sistemi in corrente alternata in modo più semplice e intuitivo rispetto all'analisi temporale diretta. Le operazioni come la derivazione e l'integrazione nel dominio del tempo si trasformano in operazioni algebriche semplici nel dominio dei fasori.

Si basa sulla formula di Eulero

$$ e^{iθ} = \cos θ + i \cdot \sin θ $$

Dove i è l'unità immaginaria i=√-1 e θ è un angolo qualsiasi.

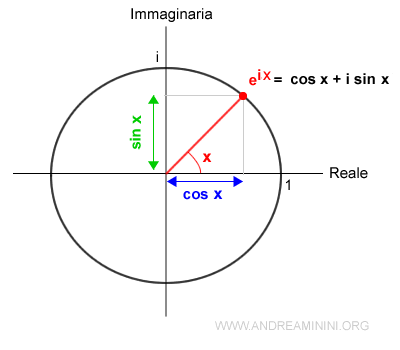
L'esponente di un numero complesso e^z è composto da una parte reale e una parte immaginaria z=x+iy

$$ e^z $$

$$ e^{x+iy} $$

$$ e^xe^{iy} $$

Il fattore e^x (parte reale di z) è il modulo (lunghezza) del vettore che congiunge l'origine con un punto della circonferenza.

L'esponente e^iy (parte immaginaria di z) è invece l'angolo θ del vettore rispetto all'asse reale x.

$$ e^x ( \cos θ + i \cdot \sin θ ) $$

Nota. Un fasore è rappresentato come un vettore nel piano complesso. La lunghezza del vettore (detta 'modulo') indica l'ampiezza della grandezza sinusoidale, mentre l'angolo x (detto 'argomento) del vettore rispetto all'asse orizzontale rappresenta la fase del segnale. La rappresentazione fasoriale non tiene conto della variazione della frequenza. Quindi, si presuppone che il segnale abbia una frequenza costante.

 

 

Un esempio pratico

Ho un segnale sinusoidale di ampiezza A basato sul coseno.

$$ A \cdot \cos θ $$

Ecco la rappresentazione del segnale sul piano cartesiano

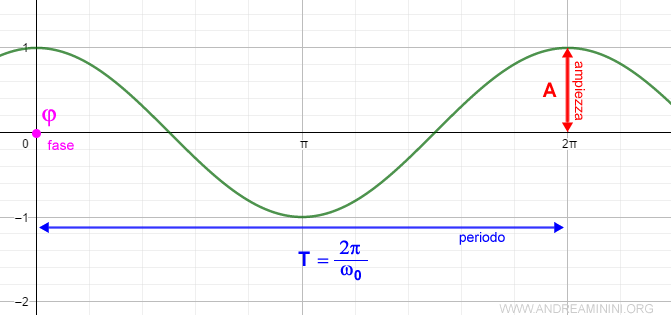
Il segnale sinusoidale A·cos θ è la parte reale di un esponenziale complesso.

$$ A \cdot R[e^{iθ}] $$

L'angolo variabile nel tempo (t) in base a una determinata pulsazione w₀ e a partire da una fase iniziale φ

$$ θ=ω_0t+φ $$

Pertanto la funzione sinusoidale del segnale diventa

$$ A \cdot R[e^{i(ω_0t+φ)}] $$

$$ A \cdot R[e^{iω_0t}e^{iφ}] $$

$$ R[A \cdot e^{iω_0t}e^{iφ}] $$

La parte reale tra parentesi quadre è un vettore rotante sul piano complesso di Gauss.

Il vettore ha un modulo (lunghezza) pari ad A e ruota in senso antiorario al variare dell'angolo θ nel tempo.

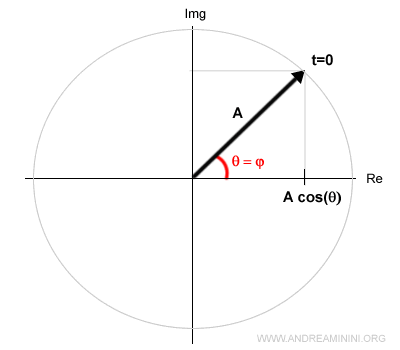
Nell'istante iniziale t=0 il vettore ha un angolo pari alla fase φ.

La proiezione del fasore sull'asse reale del piano di Gauss descrive il segnale sinusoidale.

Ad esempio, se la fase è uguale a zero (φ=0) nell'istante t=0 il segnale è pari ad A·cos(θ)=A perché l'angolo è θ=0° e il coseno di zero è 1.

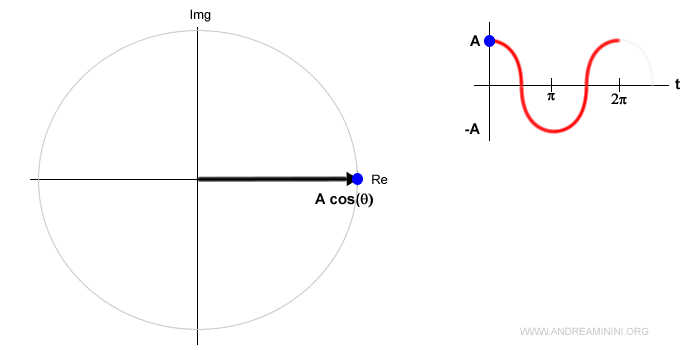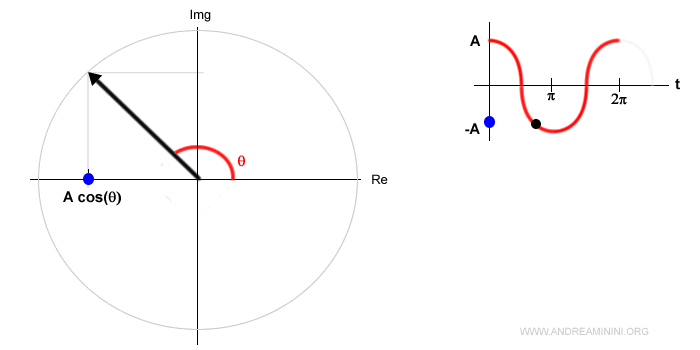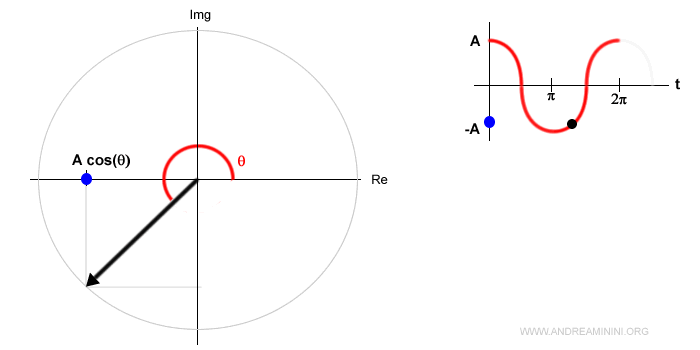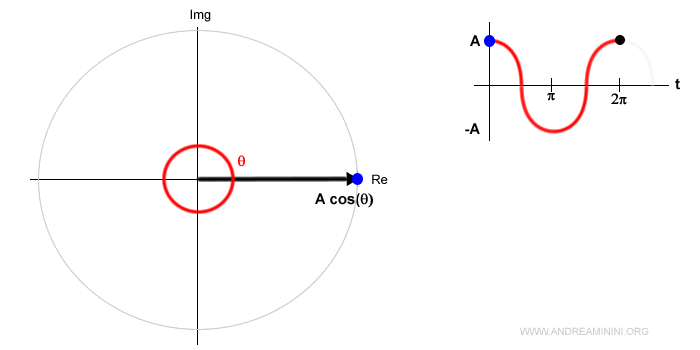
In questo esempio la proiezione è il punto di colore blu che si sposta sull'asse reale da destra a sinistra e viceversa.

E' lo stesso punto di colore blu che si sposta sull'asse verticale della rappresentazione cartesiana del segnale dall'alto al basso e viceversa.

Quindi, l'angolo θ del fasore da 0 a 2π individua un punto preciso del segnale periodico nel periodo T.

E' una relazione biunivoca.

Il fasore coniugato

Il fasore coniugato ha uguale lunghezza ma angolo e direzione di rotazione opposta.

Un fasore è associato a un numero complesso z.

Poiché ogni numero complesso z ha un numero coniugato z*, il fasore z è sempre accompagnato da un fasore coniugato z*

$$ z = A \cdot e^{if}e^{iw_0t} $$

$$ z* = A \cdot e^{-if}e^{-iw_0t} $$

Il fasore z e il fasore coniugato sono in stretta relazione con la posizione sull'asse reale Re del piano di Gauss, ossia con il segnale

$$ \frac{z+z*}{2} = A \cos θ $$

Facendo la media aritmetica dei due fasori si ottiene la parte reale del segnale.

$$ \frac{z+z*}{2} = \frac{ z \cdot e^{iφ}e^{iω_0t} + A \cdot e^{-iφ}e^{-iω_0t } }{2} $$

$$ \frac{z+z*}{2} = \frac{A}{2} \cdot e^{iφ}e^{iω_0t} + \frac{A}{2} \cdot e^{-iφ}e^{-iω_0t } $$

Nota. Nel caso di una rappresentazione del segnale sinusoidale basata sul coseno, la parte reale (Re) corrisponde al segnale stesso.

Dal punto di vista grafico la somma dei vettori la effettuo con la regola del parallelogramma

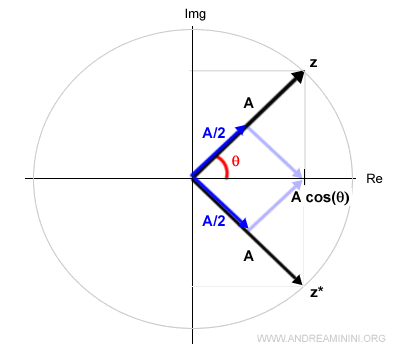
Quindi, la parte reale del segnale è

$$ \frac{z+z*}{2} = A \cos θ = \frac{A}{2} \cdot e^{iφ}e^{iω_0t} + \frac{A}{2} \cdot e^{-iφ}e^{-iω_0t } $$

Dove θ = ω₀t+φ

Questa relazione è molto utile nell'analisi dello spettro di frequenze.

Analisi nel dominio della frequenza

Un fasore è caratterizzato da tre parametri: ampiezza angolo di fase e frequenza di rotazione.

Per descrivere il fasore nel dominio della frequenza, devo associare ogni ampiezza e fase alla frequenza tramite lo spettro di frequenza.

Nota. La frequenza è il numero di giri del fasore in un secondo. E' il reciproco del periodo T. $$ f_0 = \frac{1}{T_0} = \frac{ω_0}{2π} $$

Lo spettro di frequenza è composto da due diagrammi.

• Nel primo diagramma analizzo il rapporto tra ampiezza e frequenza.
  
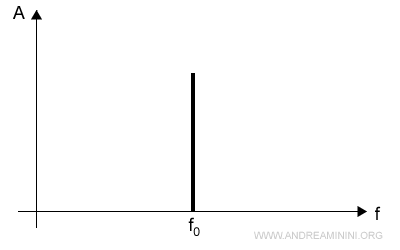
• Nel secondo diagramma analizzo il rapporto tra fase e frequenza.
  

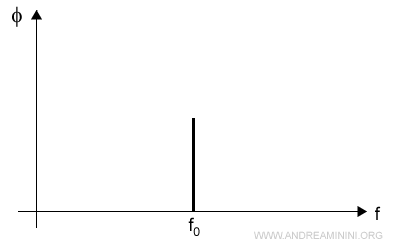
E così via.