Coppia di variabili aleatorie
Due variabili aleatorie usate in uno stesso esperimento possono avere una funzione di ripartizione congiunta $$ F(x,y) = P(X < x \ , \ Y<y) $$
Il risultato è un'intersezione degli eventi.
Esempio
La variabile aleatoria X è il punteggio del lancio di due dadi {2,3,4,5,6,7,8,9,10,11,12}.
La variabile aleatoria Y suddivide il punteggio in pari e dispari {pari,dispari}.
Questa funzione di ripartizione considera i punteggi pari sopra 6
$$ F(x,y) = P(X > 6 \ , \ Y=pari) $$
La funzione di massa di probabilità congiunta
Se le variabili aleatorie sono discrete si può anche costruire una funzione di massa di probabilità congiunta. $$ p(x_i, y_i)=P(X=x_i, Y=y_i) $$
Esempio
Il 10% delle coppie non ha figli. Il 30% delle coppie ha un figlio. Il 40% delle coppie ha due figli. Il 20% delle coppie ha tre figli.
La variabile aleatoria X indica il numero di figli maschi {0,1,2,3}
La variabile aleatoria Y indica il numero di figli femmine {0,1,2,3}.
Per assunto la probabilità di avere un figlio maschio o femmina è del 50%.
La funzione di massa di probabilità congiunta associa ai valori delle due variabili aleatorie X, Y la relativa probabilità
- Nessun figlio$$ P(X=0,Y=0)=0.10 $$
- Un figlio maschio $$ P(X=1,Y=0)=0.30 \cdot 0.5 = 0.15 $$
- Una figlia femmina $$ P(X=0,Y=1)=0.30 \cdot 0.5 = 0.15 $$
- Due figli maschi $$ P(X=2,Y=0)=0.40 \cdot 0.5^2 = 0.1 $$
- Due figlie femmine $$ P(X=0,Y=2)=0.40 \cdot 0.5^2 = 0.1 $$
- Due figli, un maschio e una femmina (2 combinazioni MF+FM) $$ P(X=1,Y=1)=2 \cdot (0.40 \cdot 0.5^2) = 0.2 $$
- Tre figli maschi $$ P(X=3,Y=0)=0.20 \cdot 0.5^3 = 0.025 $$
- Tre figli femmine $$ P(X=0,Y=3)=0.20 \cdot 0.5^3 = 0.025 $$
- Tre figli di cui due maschi e una femmina (3 combinazioni MMF+MFM+FMM) $$ P(X=2,Y=1)= 3 \cdot (0.20 \cdot 0.5^3) = 0.075 $$
- Tre figli di cui un maschio e due femmine (3 combinazioni FFM+FMF+MFF) $$ P(X=1,Y=2)=3 \cdot (0.20 \cdot 0.5^3) = 0.075 $$
Questi dati posso rappresentarli in una tabella che sintetizza l'informazione
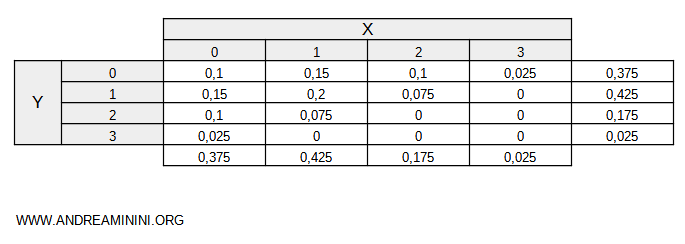
E così via.
