Dimostrazione unicità elemento neutro rispetto al prodotto
L'elemento neutro rispetto al prodotto è unico ed è il numero uno (1).$$ \exists \ 1 \in N \ | \ \forall \ a \in N \Rightarrow a \cdot 1 = a $$
Qualsiasi numero naturale moltiplicato per uno è il numero stesso.
Esempio
$$ 5 \cdot 1 = 5 $$
Dimostrazione
Devo dimostrare l'unicità dell'elemento neutro rispetto al prodotto nei numeri naturali.
Ho due possibilità
- L'elemento neutro è unico
- L'elemento neutro non è unico
Se è vera la prima affermazione, la seconda è falsa e viceversa.
Ipotizzo per assurdo che ci siano due elementi neutri 1 e ε
$$ \exists \ 1 \in N \ | \ \forall \ a \in N \Rightarrow a \cdot 1 = a $$
$$ \exists \ \epsilon \in N \ | \ \forall \ a \in N \Rightarrow a \cdot \epsilon = a $$
Essendo entrambi degli elementi neutri, quando moltiplico un numero naturale qualsiasi (a) per 1 o ε ottengo lo stesso numero naturale (a).
Quindi, se moltiplico a=1 per ε ottengo 1
$$ a \cdot \epsilon = 1 \cdot \epsilon = 1 $$
Per la stessa ragione, se moltiplico a=ε per 1 ottengo ε
$$ a \cdot 1 = \epsilon \cdot 1 = \epsilon $$
Sapendo che la moltiplicazione di due numeri naturali gode della proprietà commutativa (2° assioma dei numeri naturali).
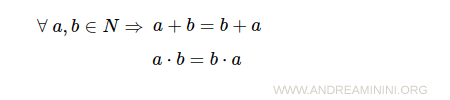
Considerando a=1 e b=ε posso scrivere la seguente uguaglianza
$$ 1 \cdot \epsilon = \epsilon \cdot 1 $$
Sapendo che 1·ε=1 e ε·1=ε
$$ \underbrace{1 \cdot \epsilon} _1 = \underbrace{ \epsilon \cdot 1 }_{ \epsilon } $$
Questo vuol dire che ε e 1 sono lo stesso numero
$$ 1 = \epsilon $$
Pertanto, nei numeri naturali non esiste un altro elemento neutro rispetto al prodotto oltre al numero uno.
Questo dimostra l'unicità dell'elemento neutro rispetto al prodotto.
E così via.
