Numeri razionali
Cosa sono i numeri razionali
L'insieme dei numeri razionali contiene tutti i numeri esprimibili tramite il rapporto di due numeri interi m,n con n diverso da zero $$ Q = \{ \frac{m}{n} : m, n \in Z, n \ne 0 \} $$ E' indicato con la lettera Q
L'insieme dei numeri razionali è composto da
- numeri interi
- numeri decimali finiti
- numeri decimali periodici
Nota. Non fanno parte dei numeri razionali i numeri decimali illimitati non periodici perché, non avendo fine, non possono essere ottenuti tramite il rapporto di due numeri interi. Questi numeri sono detti numeri irrazionali perché non sono razionali.
L'insieme dei numeri razionali comprende al suo interno l'insieme dei numeri naturali N e dei numeri interi Z.
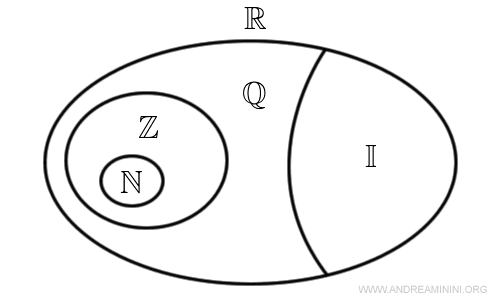
A sua volta, l'insieme dei numeri razionali è un sottoinsieme dell'insieme dei numeri reali R.
Tutti i numeri reali (R) che non appartengono all'insieme dei numeri razionali (Q) sono detti numeri irrazionali (I).
Un esempio pratico
Esempio 1
Il numero 2.5 è un numero razionale perché si può esprimere tramite il rapporto di due numeri interi m=5 e n=2
$$ 2.5 = \frac{5}{2} \in Q $$
Esempio 2
Il numero 5 è un numero naturale e intero ma è anche un numero razionale perché si può esprimere con la divisione di 15 per 3
$$ 5 = \frac{15}{3} \in Q $$
Nota. Qualsiasi numero naturale o intero può essere ottenuto tramite il rapporto di due numeri interi. Pertanto, i numeri naturali e i numeri interi sono sottoinsiemi dei numeri razionali.
Esempio 3
Anche i numeri decimali periodici sono numeri razionali perché posso ottenerli tramite il rapporto di due numeri interi
$$ 3.\bar{3} = \frac{10}{3} \in Q $$
Le operazioni tra numeri razionali
Nell'insieme dei numeri razionali sono utilizzabili le seguenti operazioni
- Addizione
$$ a+b = c \ \ \ \ a,b,c \in Q $$ - Sottrazione
$$ a-b = c \ \ \ \ a,b,c \in Q $$ - Moltiplicazione
$$ a \cdot b = c \ \ \ \ a,b,c \in Q $$ - Divisione
$$ a : b = c \ \ \ \ a,b \in Q \ c \in Q $$ - Potenza
$$ a^b = c \ \ \ \ a,b \in Q \ c \in Q $$
Nota. L'addizione, la sottrazione, la moltiplicazione e la divisione sono operazioni interne all'insieme dei numeri razionali Z, perché il risultato è sempre un numero razionale.
La rappresentazione dei numeri razionali
Per rappresentare i numeri razionali disegno una retta a cui fisso un verso, punto di origine (O) e un'unità di misura.
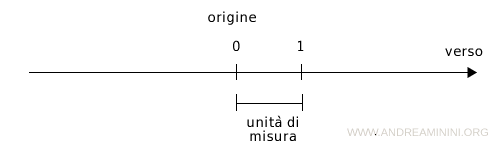
Dopo aver disegnato la retta associo i numeri razionali ai relativi punti della retta.
Ad esempio, tutte le frazioni con denominatore uguale a 1 individuano alcuni punti della retta.
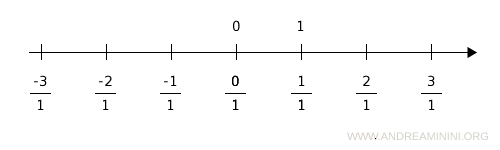
Le frazioni con denominatore uguale a 2 individuano altri punti della retta.
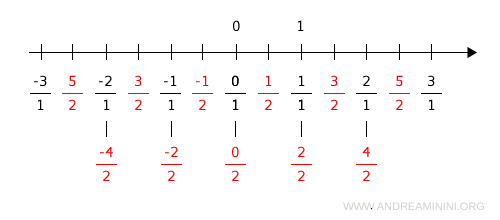
Tuttavia, alcuni punti sono gli stessi.
Ad esempio, i numeri razionali 1/1 e 2/2 sono associati allo stesso punto della retta.
Lo stesso accade per i punti 0/1 e 0/2 oppure 2/1 e 4/2 e via dicendo.
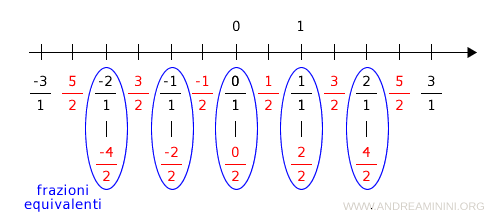
Questo accade perché un numero razionale può essere rappresentato da infinite frazioni equivalenti che individuano lo stesso punto della retta.
Continuando a inserire i numeri razionali sulla retta balza all'occhio un'altra proprietà dei numeri razionali.
Tra due diversi numeri razionali esistono infiniti altri numeri razionali intermedi.
Per indicare questa proprietà si dice che l'insieme dei numeri razionali è un insieme denso.
Ad esempio, scelgo i numeri razionali 1/2 e 1/4

Tra questi c'è sicuramente un punto medio
$$ \frac{ \frac{1}{2} + \frac{1}{4} }{2} = \frac{ \frac{2+1}{4} }{2} = \frac{ \frac{3}{4} }{2} = \frac{3}{4} \cdot \frac{1}{2} = \frac{3}{8} $$
Il numero razionale 3/8 è un punto intermedio che si trova esattamente alla stessa distanza tra 1/2 e 1/4
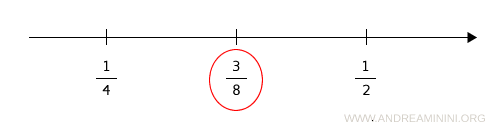
Tra 3/8 e 1/2 c'è sicuramente un altro punto medio
$$ \frac{ \frac{3}{8} + \frac{1}{2} }{2} = \frac{ \frac{3+4}{8} }{2} = \frac{ \frac{7}{8} }{2} = \frac{7}{8} \cdot \frac{1}{2} = \frac{7}{16} $$
Il numero razionale 7/16 si trova alla stessa distanza tra 1/2 e 3/8
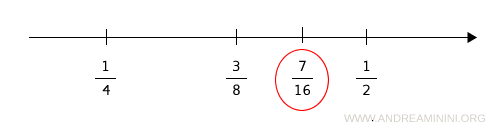
Continuando troverei altri infiniti punti sempre più vicini a 1/2 ma mai uguali a 1/2
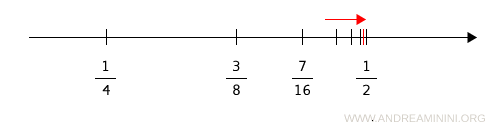
La stessa coda accade anche a destra del punto 1/2
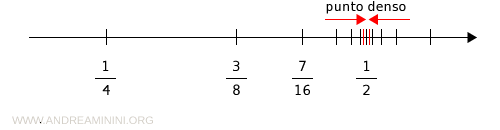
In questi casi si dice che il punto 1/2 è un punto denso.
Lo stesso ragionamento vale per tutti gli altri numeri razionali. Ogni numero razionale è un punto denso della retta.
A questo punto si potrebbe pensare che tutti i punti della retta sono numeri razionali ma non è così.
L'insieme dei numeri razionali è un insieme infinito e per ogni numero razionale esiste uno e un solo punto sulla retta.
Tuttavia, questa non è una relazione biunivoca.
Esistono dei punti della retta che non sono numeri razionali.
Ad esempio, la radice quadrata di 2 è un punto della retta.
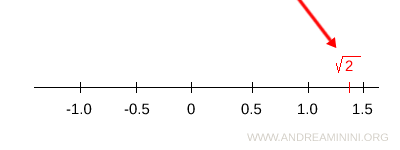
Tuttavia, non esiste nessun numero razionale uguale alla radice quadrata di 2 (vedi dimostrazione).
$$ \sqrt{2} \notin Q $$
Pertanto, i numeri razionali non mi permettono di disegnare tutti i punti di una retta.
Sulla retta rimarrebbero comunque dei "buchi". Infiniti buchi.
Per coprire anche questi buchi devo ricorrere a un altro insieme numerico, l'insieme dei numeri irrazionali.
La differenza tra numeri razionali e irrazionali
L'insieme dei numeri razionali è composto da numeri decimali finiti e da numeri decimali periodici. Non include anche i numeri illimitati non periodici.
L'insieme dei numeri razionali è chiuso alle operazioni di addizione, sottrazione, moltiplicazione e divisione esclusa la divisione per zero.
Tuttavia, l'operazione inversa della potenza, ossia la radice quadrata o ennesima, non è un'operazione interna ai numeri razionali.
In alcuni casi, la radice è un numero decimale illimitato non periodico.
I numeri decimali illimitati non periodici sono detti numeri irrazionali perché non appartengono all'insieme dei numeri razionali.
Esempio 4
La radice di 2 è un numero decimale illimitato non periodico.
$$ \sqrt{2} \notin Q $$
Non è un numero razionale perché non esistono due numeri interi m,n tali che il loro rapporto dia come risultato √2.
Esempio 5
Un altro esempio di numero decimale illimitato non periodico è il pi greco.
$$ 3,14159265358979323846... $$
Non posso ottenere il pi greco come rapporto di due numeri interi. Pertanto, non è un numero razionale.
La radice quadrata nei numeri razionali
La radice quadrata è l'operazione inversa dell'elevamento al quadrato e non è un'operazione interna dei numeri razionali.
La radice quadrata di un numero n positivo o nullo è un numero m che elevato al quadrato restituisce il numero n
$$ \sqrt{n} = m \Leftrightarrow m^2 =n $$
Ad esempio, la radice quadrata di 25 è uguale a ±5
$$ \sqrt{25} = \pm 5 $$
perché ci sono due numeri 5 e -5 che moltiplicati per se stessi danno come risultato 25
$$ 5 \cdot 5 = 25 $$
$$ (-5) \cdot (-5) = 25 $$
Nota. Per convenzione si sceglie la radice positiva $$ \sqrt{25} = 5 $$ Nel caso della risoluzione di un'equazione vanno considerate entrambe le radici.
La radice quadrata del numero zero è zero.
$$ \sqrt{0} = 0 $$
La radice quadrata non è invece definita nei numeri razionali negativi.
Esempio. La radice quadrata di -25 non esiste $$ \sqrt{-25} $$ perché nessun numero elevato al quadrato è negativo.
Perché la radice quadrata non è un'operazione interna dei numeri razionali?
La radice quadrata non è un'operazione interna dei numeri razionali perché la radice di alcuni numeri razionali non è a sua volta un numero razionale.
Esempio. Il numero 2 è un numero razionale $$ 2 \in Q $$ La radice quadrata di 2 esiste ma non è un numero razionale. Vedi dimostrazione. $$ \sqrt{2} \notin Q $$ La radice quadrata di 2 è un numero irrazionale.
I numeri razionali e i punti della retta
Ogni numero razionale è un punto della retta ma non tutti i punti della retta sono numeri razionali.
L'insieme dei numeri razionali è un insieme denso ma non completo.
E' un insieme denso perché dati due numeri razionali a/b e c/d è sempre possibile trovare un altro numero razionale (a+b)/(c+d) tra di essi.
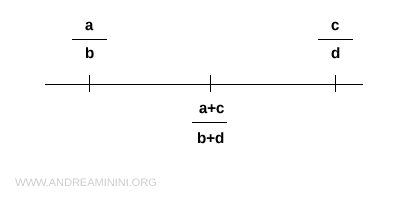
L'insieme dei numeri razionali non è un insieme completo perché non può essere messo in corrispondenza biunivoca con i punti della retta.
Dimostrazione
A ogni numero razionale corrisponde un punto della retta.
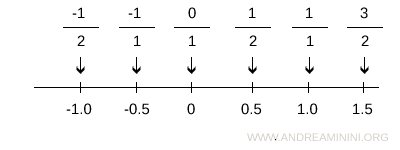
Per dimostrare che non tutti i punti della retta sono numeri razionali, mi basta trovare un punto della retta a cui non corrisponde nessun numero razionale.
Ad esempio, la radice quadrata di due è un punto della retta ma non è un numero razionale (vedi dimostrazione).

Nota. Oltre alla radice quadrata di due ci sono altri infiniti punti della retta "irrazionali" (non razionali) ma in questo caso è sufficiente trovarne uno per completare la dimostrazione.
Pertanto, i numeri razionali sono un sottoinsieme dei punti della retta.
Per trovare una corrispondenza biunivoca tra un insieme numerico e i punti della retta devo estendere l'insieme numerico ai numeri reali.
E così via.
