Numeri iperreali
I numeri iperreali sono un insieme numerico composto dai numeri reali (R), dai numeri infinitamente grandi ∞ (infiniti) e da quelli infinitamente piccoli ε (infinitesimali).
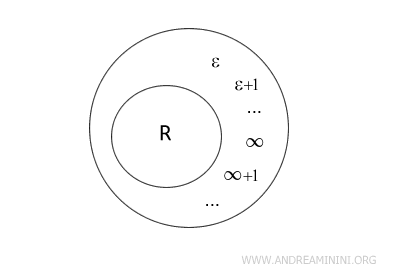
L'insieme dei numeri iperreali è ovviamente più esteso dei numeri reali (R) perché vi aggiunge altri due sottoinsiemi
- Numeri infiniti
I numeri infiniti sono quei numeri maggiori di qualsiasi numero reale o minori di qualsiasi numero reale. $$ \forall \ x \in R \ \Rightarrow \ \infty > x \ $$ - Numeri infinitesimi
I numeri infinitesimi sono quei numeri minori di ogni numero reale positivo e maggiori di ogni numero reale negativo. Pertanto, i numeri infinitesimi posso considerarli come reciproci dei numeri infiniti ε=1/∞ e viceversa. $$ \forall \ x \in R^+ \ \Rightarrow \ \epsilon < x \ $$
Pur non essendo uno spazio metrico, l'insieme dei numeri iperreali ha una topologia che permette l'ordinamento dei numeri iperreali.
A differenza dei numeri reali, nei numeri iperreali gli infiniti non sono solo dei simboli e possono essere ordinati come veri e propri numeri.
$$ \infty < \infty + 1 < \infty +2 < ... $$
Se ∞ è un numero infinito, allora lo è anche ∞+1 è un infinito ed è maggiore di ∞.
Lo stesso ragionamento vale per i numeri infinitesimi essendo questi ultimi un reciproco degli infiniti ε=1/∞.
$$ 0 < \epsilon < \epsilon + 1 < \epsilon +2 < ... $$
Se ε è un numero infinitesimo diverso da zero, allora è minore di ε+1. E via dicendo.
In altre parole, l'infinito ∞ e l'infinitesimo ε non sono considerati come simboli ma come numeri veri e propri, e come tali possono essere usati come operandi nelle operazioni matematiche.
Un esempio pratico
Considero una retta tangente a una circonferenza in un punto.
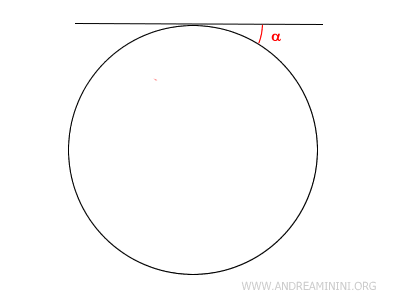
Qual è l'angolo tra la retta tangente e la circonferenza?
L'angolo non può essere zero perché, in questo caso, i lati dell'angolo sarebbero coincidenti.
D'altra parte l'angolo non può essere nemmeno maggiore di zero, perché allora la retta sarebbe secante alla circonferenza e non tangente.
In questi casi si assume che l'angolo tra la retta tangente e la circonferenza sia un infinitesimo (ε).
$$ \alpha = \epsilon $$
Quindi, l'infinitesimo esiste e non è un'astrazione.
Tuttavia, l'infinitesimo (ε) non è considerato un numero reale nel calcolo infinitesimale di fine ottocento (analisi standard), quello di Karl Weierstrass su cui si basano gli esami di analisi matematica 1 e 2 all'università.
Nel corso del XX secolo alcuni matematici hanno cominciato a chiedersi se l'infinitesimo non meriti d'essere trattato come numero, anziché come simbolo.
Da questa ipotesi è nata l'analisi non standard del calcolo infinitesimale.
Nota. Nell'ambito dell'analisi non-standard l'infinitesimo è un numero e può essere visto come il rapporto con un numero infinitamente grande al denominatore $$ \epsilon = \frac{1}{\infty} $$ Quindi, se l'infinitesimo è un numero (ε), allora lo è anche l'infinito (∞). Non potendo essere definiti numeri reali... sono stati battezzati come numeri iperreali, un insieme numerico molto più grande che include i numeri reali (R), tutti gli infinitesimi (ε) e tutti gli infiniti (∞).

Il campo dei numeri iperreali
I numeri iperreali formano un campo ordinato detto campo dei numeri iperreali.
Il campo dei numeri reali è un sottocampo del campo dei numeri iperreali.
Nota. Il concetto dei numeri iperreali è oggetto di studio dell'analisi matematica non standard. Venne introdotto per la prima volta nel 1966 da Abraham Robinson dell'università Yale nel libro Non-Standard Analysis. I numeri iperreali non vanno confusi con i numeri surreali. Entrambi i sistemi offrono metodi unici per esplorare concetti infiniti e infinitesimali, ma i loro ambiti di applicazione e le tecniche matematiche sono distinte. Vedi differenza tra numeri surreali e iperreali.
E così via.
