Insieme dei numeri interi non negativi

L'insieme dei numeri interi non negativi è l'unione dell'insieme dei numeri naturali e dello zero. Si indica con il simbolo N₀ $$ N_0 = N \cup \{ 0 \} $$

E' composto da tutti i numeri interi non negativi a partire da zero

$$ N_0 = \{ \ 0 \ , \ 1 \ , \ 2 \ , \ 3 \ , \ ... \ \} $$

L'insieme dei numeri interi non negativi N₀ include l'insieme dei numeri naturali N.

$$ N_0 ⊂ N $$

Quindi, l'insieme N₀ rispetta i cinque assiomi dei numeri naturali.

1. L'insieme dei numeri naturali è chiuso rispetto alla somma e al prodotto
   
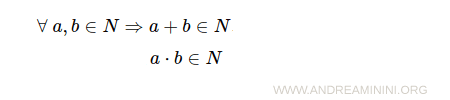
2. Proprietà commutativa della somma e del prodotto
   
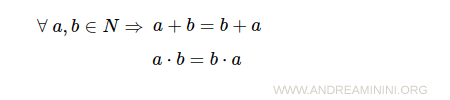
3. Proprietà associativa della somma e del prodotto
   
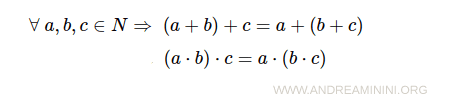
4. Proprietà distributiva della somma e del prodotto
   
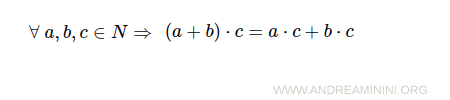
5. Esistenza di un elemento neutro rispetto al prodotto

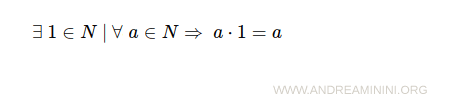
A questi devo aggiungere un sesto assioma per definire l'insieme dei numeri interi non negativi

6. assioma dell'elemento neutro rispetto alla somma.
   La somma di qualsiasi numero intero non negativo con zero è uguale al numero stesso. $$ \exists \ 0 \in N_0 \ | \ \forall \ a \in N_0 \Rightarrow a+0=a $$

   Esempio. La somma 5+0 è uguale a 5 $$ 5+0 = 5$$

Osservazioni utili

Alcune osservazioni utili sui numeri interi non negativi

• L'elemento neutro rispetto alla somma è il numero zero
  Qualsiasi numero intero non negativo sommato a zero è il numero stesso. $$ \forall \ a \in N_0 \Rightarrow a + 0 = a $$
• L'elemento neutro rispetto alla somma è unico
  Non esistono altri elementi neutri rispetto alla somma oltre lo zero.

  Dimostrazione. Per dimostrare l'unicità dell'elemento neutro faccio un ragionamento per assurdo. Ci sono due possibilità:
  
  1) l'elemento neutro è unico
  2) l'elemento neutro non è unico
  
  Se per ci fosse un secondo elemento neutro ε oltre a zero varrebbe la condizione $$ \exists \ \epsilon \in N_0 \ | \ \forall \ a \in N_0 \Rightarrow a + \epsilon = a $$ oltre alla condizione $$ \exists \ 0 \in N_0 \ | \ \forall \ a \in N_0 \Rightarrow a + 0 = a $$ Essendo entrambi elementi neutri, sommando zero a qualsiasi numero di N ottengo lo stesso numero. $$ a+0=a $$ Allo stesso modo sommando 𝜺 a qualsiasi numero di N ottengo lo stesso numero $$ a+ \epsilon = a $$ Quindi, se considero a=ε e sommo lo zero ottengo ε. $$ a+0=\epsilon + 0 = \epsilon $$ Se considero a=0 e sommo ε ottengo zero $$ a+\epsilon = 0 + \epsilon = 0 $$ In base al secondo assioma dei numeri naturali vale la proprietà commutativa della somma x+y=y+x. Pertanto $$ \epsilon + 0 = 0 + \epsilon $$ Sapendo che ε+0=ε e 0+ε=0 $$ \underbrace{ \epsilon + 0 }_{\epsilon} = \underbrace{0 + \epsilon}_0 $$ ne consegue che $$ \epsilon = 0 $$ Questo vuol dire che 𝜺 è 0. Pertanto, negli interi non negativi N₀ non esiste un altro elemento neutro rispetto alla somma oltre allo zero. Questo dimostra l'unicità dell'elemento neutro rispetto alla somma.

• Qualsiasi numero intero non negativo moltiplicato per zero è uguale a zero $$ \forall \ a \in N_0 \Rightarrow a \cdot 0 = 0 $$

  Dimostrazione. Per il quinto assioma dei numeri naturali qualsiasi numero naturale (N) moltiplicato per 1 è uguale al numero stesso perché 1 è l'elemento neutro del prodotto $$ a = a \cdot 1 $$ Utilizzo il sesto assioma dei numeri interi non negativi (N₀) per riscrivere 1=1+0 come somma di uno e zero $$ a = a \cdot 1 = a \cdot (1 + 0) $$ Applico la proprietà distributiva dei numeri naturali (quarto assioma) $$ a = a \cdot 1 = a \cdot (1 + 0) = a \cdot 1 + a \cdot 0 $$ Sapendo che il numero 1 è l'elemento neutro del prodotto (quinto assioma) posso riscrivere a·1=a $$ a = a \cdot 1 = a \cdot (1 + 0) = a \cdot 1 + a \cdot 0 = a + a \cdot 0 $$ Questo vuol dire che a=a+a·0 $$ a = a+a \cdot 0 $$ Per essere soddisfatta l'identità a=a il secondo addendo a·0 deve comportarsi come l'elemento neutro della somma (sesto assioma). $$ a = a+\underbrace{a \cdot 0}_0 $$ Sapendo che l'elemento neutro della somma è unico ed è zero, il termine a·0 è uguale a zero $$ a \cdot 0 = 0 $$ Pertanto, qualsiasi numero intero non negativo moltiplicato per zero è uguale a zero $$ \forall \ a \in N_0 \Rightarrow a \cdot 0 = 0 $$

E così via.