Numeri surreali
Cosa sono i numeri reali
I numeri surreali sono un campo che contiene i numeri reali, i numeri infiniti e i numeri infinitesimi.
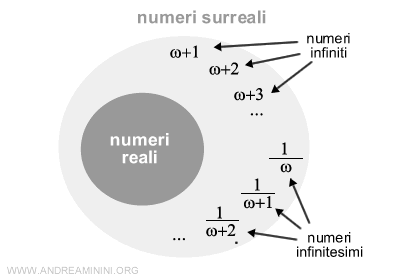
Si chiamano così perché sono sopra i numeri reali.
I numeri surreali furono ideati da John Horton Conway.
Tuttavia, il termine "surreal number" venne coniato nel 1974 da Donald Knuth nel libro "Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness".
Nota. E' un libro originale che racconta la matematica come fosse un dialogo tra due persone ma senza dimenticare la classica notazione matematica. C'è anche la versione italiana.
L'insieme dei numeri surreali è più grande rispetto all'insieme dei numeri reali perché contiene oltre ai numeri reali anche
- i numeri infiniti
ogni numero maggiore di qualunque numero reale in valore assoluto - i numeri infinitesimi
ogni numero minore di qualunque numero reale in valore assoluto
Ogni numero surreale è associato a due insiemi detti insieme sinistro L e insieme destro.
Su questo semplice concetto si fonda l'intera costruzione dell'insieme dei numeri surreali.
Le regole di Conway
Per definire i numeri surreali bisogna seguire due regole dette regole di Conway.
- Ogni numero surreale è associato a due insiemi L, R
Nessun elemento dell'insieme L è maggiore o uguale a qualsiasi elemento dell'insieme R. $$ x_L \ngeq x_R \ \ \ x_L \in X_L \ , \ x_R \in X_R $$ E viceversa, nessun elemento dell'insieme R è minore o uguale a qualsiasi elemento dell'insieme L. $$ x_R \nleq x_L \ \ \ x_L \in X_L \ , \ x_R \in X_R $$Nota. Pertanto, l’insieme L (left) contiene tutti i numeri minori del numero surreale ed è detto insieme sinistro del numero. L’insieme R (right) contiene tutti i numeri maggiori del numero surreale ed è detto insieme destro del numero. In genere, per definire un numero surreale x si usa la notazione $$ x = \{ X_L | X_R \} $$ oppure come una coppia $$ x = (X_L, X_R) $$ o in alternativa $$ x = < X_L \ | \ X_R > $$ Dove XL è l’insieme sinistro e XR è l’insieme destro di x.
- Regola di confronto
Dati due numeri surreali x = { XL | XR } e y = { YL | YR } vale la relazione d’ordine x ≤ y se e solo se- nessun elemento di XL è maggiore o uguale di y $$ x_L \ngeq y \ \ \ x_L \in X_L $$
- nessun elemento di YR è minore o uguale di x $$ y_R \nleq x \ \ \ y_R \in Y_R $$
Con queste due regole posso cominciare a definire i numeri.
Come costruire l'insieme dei numeri surreali
Inizialmente, non esiste nessun numero.
Quindi l’insieme sinistro e l’insieme destro sono insiemi vuoti.
$$ L = \{ \} $$ $$ R = \{ \} $$
Per semplificare la notazione e ridurre il numero di parentesi graffe, d'ora in poi indico l'insieme vuoto con il simbolo Ø.
$$ L = Ø $$ $$ R = Ø $$
Nota. I due insiemi L e R sono insiemi vuoti ma rispettano entrambe le regole dei numeri surreali. In effetti, nessun elemento di L è maggiore o uguale degli elementi di R. $$ x_L \ngeq x_R \ \ \ x_L \in X_L \ , \ x_R \in X_R $$
A questo punto definisco il primo numero surreale ossia il numero zero.
Al momento lo zero non ha altri numeri né a sinistra (L), né a destra (R).
Quindi posso scriverlo come coppia di insiemi vuoti.
$$ 0 = (Ø, Ø) $$
In questa prima iterazione ho creato un solo numero, lo zero.
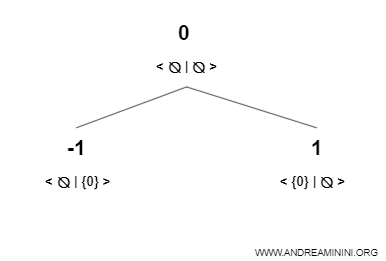
Ora usando lo numero zero (0) e l'insieme vuoto Ø posso generare altri due nuovi numeri.
Il numero 1 ha lo zero {0} nell'insieme sinistro (L) e l'insieme vuoto Ø nell'insieme destro (R).
$$ 1 = (\{ 0 \}, Ø) $$
Nota. Gli insiemi L e R del numero 1 rispettano le regole dei numeri surreali. Nessun elemento di L={0} è maggiore o uguale degli elementi di R=Ø. $$ x_L \ngeq x_R \ \ \ x_L \in X_L \ , \ x_R \in X_R $$
L'altro numero è il numero -1 che ha lo zero {0} nell'insieme destro (R) e l'insieme vuoto Ø nell'insieme sinistro (L).
$$ -1 = (Ø, \{ 0 \}) $$
Nota. Gli insiemi L e R del numero -1 rispettano le regole dei numeri surreali. Nessuno degli elementi dell'insieme destro R è maggiore o uguale agli elementi dell'insieme sinistro L. $$ x_L \ngeq x_R \ \ \ x_L \in X_L \ , \ x_R \in X_R $$ In generale, se uno dei due insiemi L e/o R è un insieme vuoto, le regole dei numeri surreali sono sempre soddisfatte.
In questa seconda iterazione ho creato altri 2 nuovi numeri.
L'insieme dei numeri surreali è già composto da tre numeri {-1, 0, 1}.
Ogni numero è a sua volta associato da due insiemi: l'insieme sinistro L e l'insieme destro R.
In una terza iterazione utilizzo i numeri conosciuti {-1, 0, 1} per crearne altri.
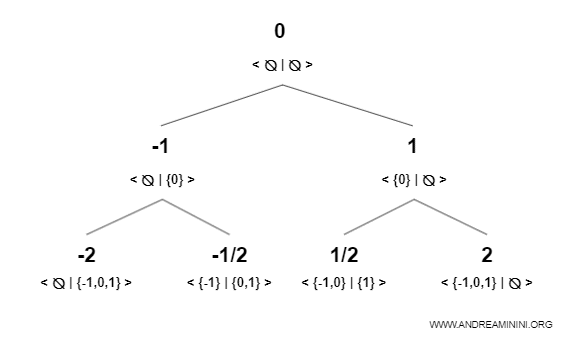
Nota. Il numero -2 ha l'insieme vuoto Ø a sinistra (L) e l'insieme {-1,0,1} a destra (R). $$ -2 = (Ø, \{ -1, 0, 1 \}) $$ Il numero -1/2 ha l'insieme {-2} a sinistra (L) e l'insieme {0,1} a destra (R). $$ -1/2 = (\{ -1 \} , \{ 0, 1 \}) $$ Il numero 1/2 ha l'insieme {-1,0} a sinistra (L) e l'insieme {1} a destra (R). $$ 1/2 = (\{ -1, 0 \} , \{ 1 \}) $$ Il numero 2 ha l'insieme {-1,0, 1} a sinistra (L) e l'insieme vuoto Ø a destra (R). $$ 2 = (\{ -1, 0, 1 \} , \{ Ø \}) $$
In questa iterazione ho creato altri 4 nuovi numeri.
I numeri surreali dell'universo sono diventati sette
$$ \{-2 \ , \ -1 \ , \ - \frac{1}{2} \ , \ 0 \ , \ \frac{1}{2} \ , \ 1 \ , \ 2 \} $$
In una quarta iterazione utilizzo i numeri surreali conosciuti per crearne altri.
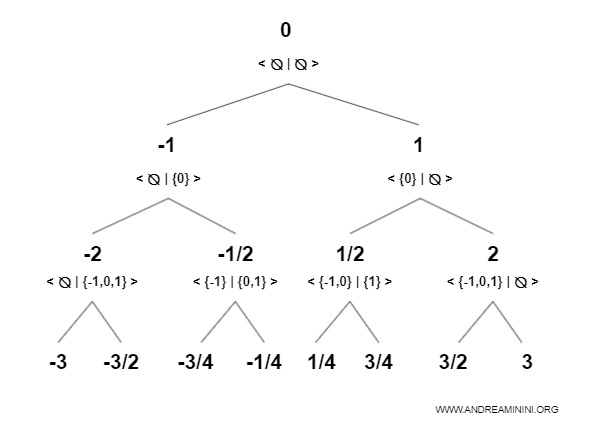
Nella quarta iterazione ho creato altri 8 nuovi numeri.
Ora i numeri dell'universo sono diventati quindici.
Nota. Si verifica una sorta di Big Bang nella creazione dei numeri surreali che parte dall'insieme vuoto fino a raggiungere l'infinito ...e oltre. Alla prima iterazione ho creato un numero (0), alla seconda iterazione ho creato due numeri (1,-1), alla terza iterazione ho creato quattro numeri (-2,-1/2, 1/2, 2), alla quarta iterazione ho creato otto numeri. E' una successione divergente. Ogni iterazione k-esima genera 2k nuovi numeri. $$ 2^k = 2^0 \ , \ 2^1 \ , \ 2^2 \ , \ 2^3 \ , \ 2^4 \ , .... $$ $$ 2^k = 1 \ , \ 2 \ , \ 4 \ , \ 8 \ , \ 16 \ , \ 32 \ , \ 64 \ , \ 128 \ , \ 256 \ , \ .... $$ Dopo ogni iterazione l'universo dei numeri surreali aumenta seguendo il passo di una serie geometrica anch'essa divergente. $$ \sum_{k=0}^{\infty} 2^k = 1+2+2^2+...+2^k $$
Ripetendo l'iterazione all'infinito definisco tutti gli infiniti numeri dell'insieme dei numeri razionali (Q) ossia i numeri definiti dal rapporto di due numeri interi (m/n).
$$ 0 \ , \ \pm 1 \,\ \pm \frac{1}{2} \,\ \pm \frac{1}{3} \,\ \pm \frac{1}{4} \,\ \pm \frac{1}{5} \,\ ... \,\ \pm \infty $$
Se l'insieme dei numeri surreali comprende i numeri razionali allora include anche i numeri irrazionali (I), perché tutti i numeri irrazionali possono essere definiti tra due insiemi L e R di numeri razionali.
$$ \sqrt{2} \ , \ \sqrt{3} \ , \ \sqrt{4} \ , \ \pi \ ... $$
Ad esempio, la radice di 2 e π posso scriverli come numeri surreali in questo modo
$$ \sqrt{2} = ( \{ 1 \, \ 1.4 \ , \ 1.41 \ , \ 1.414 \ , \ ... \} \ , \{ 2 \, \ 1.5 \ , \ 1.42 \ , \ 1.415 \ , \ ... \} ) $$
$$ \pi = ( \{ 3 \ , \ 3.1 \ , \ 3.14 \ , \ 3.141 \ , \ 3.1415 \ , \ ... \} \ , \{ 4 \, \ 3.2 \ , \ 3.15 \ , \ 3.142 \ , \ 3.1416 \ , \ ... \} ) $$
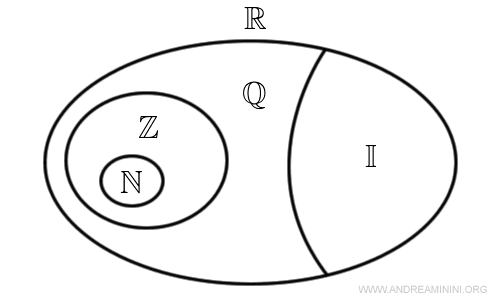
A questo punto, se l'insieme dei numeri surreali include al suo interno sia i numeri razionali (Q) che irrazionali (I), allora comprende l'insieme dei numeri reali (R).
A questo punto definisco l'infinito dei numeri reali (∞) e lo indico nei numeri surreali con il simbolo omega ω.
$$ \omega = (\{ 0,1, 2, ... \} \ | | Ø ) $$
Il numero surreale ω ha l'insieme dei numeri reali come insieme sinistro (L) e l'insieme vuoto Ø come insieme destro (R).
$$ \omega = ( \ R \ | \ Ø \ ) $$
Nota. Allo stesso modo definisco anche meno infinito dei numeri reali (-∞). E' il numero surreale -ω che ha l'insieme vuoto Ø a sinistra (L) e l'insieme dei numeri reali a destra (R). $$ - \omega = ( \ Ø \ | \ R \ ) $$
E quì succede qualcosa di interessante.
Seguendo le regole di Conway posso compiere un'ulteriore iterazione usando il simbolo dell'infinito ω.
L'iterazione successiva crea altri numeri surreali tra i quali soprattutto due sono importanti
- Infinito più uno
L'infinito più uno è un numero surreale che ha l'infinito ω (∞) nell'insieme sinistro (L) e l'insieme vuoto Ø nell'insieme destro (R). E' quindi un numero più grande di infinito.
$$ \omega + 1 = ( \omega \ | \ Ø \ ) $$ - Infinitesimo
L'infinitesimo (ε) è un numero surreale che ha lo zero nell'insieme sinistro (L) e 1/ω nell'insieme destro (R). E' un numero più grande di zero e più piccolo di qualsiasi altro numero reale.
$$ \epsilon = ( 0 \ | \ \frac{1}{ \omega } ) $$
Pertanto, l'insieme di numeri surreali è più grande dell'insieme dei numeri reali (R) perché contiene anche dei numeri infiniti e dei numeri infinitesimi.

Ovviamente non finisce qui.
Iterando di nuovo trovo anche infiniti più grandi (ω+2) e infinitesimi più piccoli 1/(ω+1).
$$ \omega + 2 = ( \omega + 1 \ | \ Ø \ ) $$
$$ \omega + 3 = ( \omega + 2 \ | \ Ø \ ) $$
$$ \omega + 4 = ( \omega + 3 \ | \ Ø \ ) $$
$$ \vdots $$
In conclusione, i numeri surreali permettono di definire altri concetti matematici come l'infinito di infinito, il confronto tra gli infiniti o tra gli infinitesimi, ecc.
Tutti concetti già noti nella teoria matematica ma non facilmente ottenibili con i numeri reali.
E così via.
