Numeri irrazionali

Cosa sono i numeri razionali

L'insieme dei numeri irrazionali è composto da tutti i numeri reali non esprimibili come rapporto di due numeri interi.

L'insieme dei numeri irrazionali è composto da numeri decimali illimitati non periodici.

Una parte dei numeri irrazionali derivano dall'estrazione della radice (es. √2, √3, √5, √7,...).

Un'altra parte, invece, non deriva dalle radici (es. la costante pi greco π=3,14159... è il rapporto tra la circonferenza e il diametro di un cerchio).

Perché si chiamano irrazionali

Il termine "irrazionale" deriva dalla contrapposizione dei numeri razionali.

Cosa sono i numeri razionali? Un numero reale (R) è detto razionale (Q) se è esprimibile tramite il rapporto di due numeri interi. Ad esempio, il numero reale 2.5 è razionale perché si ottiene con la divisione 5/2. Tuttavia, non tutti i numeri reali sono ottenibili dal rapporto di due numeri interi.

Tutti i numeri reali che non sono razionali sono detti irrazionali (I).

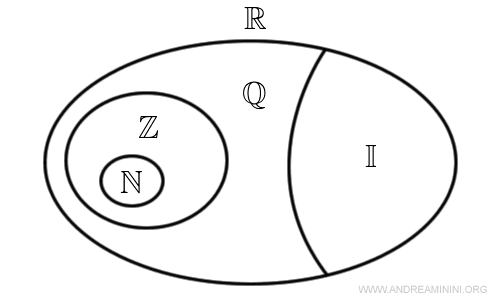
Un esempio pratico

La radice quadrata del numero 3 è un numero reale.

$$ \sqrt{3} = 1.73205080757 \in R $$

Tuttavia, non può essere espresso come rapporto di due numeri interi.

Nessuna coppia di numeri interi m,n dà come risultato la radice quadrata di 3.

$$ \frac{m}{n} = \sqrt{3} $$

Pertanto, √3 non è un numero razionale.

$$ \sqrt{3} \notin Q $$

La radice quadrata di 3 è un numero irrazionale.

$$ \sqrt{3} \in I $$

Nota. Lo stesso discorso vale per altre radici non risolvibili alla seconda, alla terza, ecc. $$ \sqrt{7} \\ \sqrt[3]{5} \\ \sqrt[4]{6} \\ \vdots $$ Il discorso però non vale in generale per tutte le radici, perché alcune radici appartengono all'insieme dei numeri razionali. Ad esempio $$ \sqrt{9} = 3 = \frac{6}{2} $$ Inoltre, alcune radici non appartengono all'insieme dei numeri reali. Quindi non sono né razionali, né irrazionali. Ad esempio, nessun numero reale moltiplicato per se stesso dà come risultato -1. $$ \sqrt{-1} \notin R $$ Quest'ultima radice appartiene all'insieme dei numeri complessi.

Come capire se un numero è irrazionale

Per capire se un numero è irrazionale posso usare il metodo delle approssimazioni successive.

Ad esempio, devo capire se la radice quadrata di due è un numero irrazionale

$$ \sqrt{2}$$

Individuo due numeri interi il cui quadrato approssimano la radice quadrata di 2 per difetto e per eccesso

$$ 1 < \sqrt{2} < 2 $$

Nota. Per cercare questi due numeri elevo tutti i membri della disequazione per due. $$ x \le \sqrt{2} \le y $$ $$ x^2 \le ( \sqrt{2} )^2 \le y^2 $$ $$ x^2 \le 2 \le y^2 $$ Poi cerco due numeri x e y che approssimano meglio per difetto e per eccesso due. In questo caso x=1 e y=2 $$ 1^1 \le 2 \le 2^2 $$

In seconda approssimazione cerco due numeri con una cifra decimale che approssimano meglio √2 per difetto e per eccesso

$$ 1.4 < \sqrt{2} < 1.5 $$

Nota. Per trovare questi altri due numeri parto dall'estremo inferiore precedente (1) e aggiungo man mano una cifra decimale finché il suo quadrato supera due. $$ 1.0^2 = 1 \\ 1.1^2=1.21 \\ 1.2^2 = 1.44 \\ 1.3^2=1.69 \\ 1.4^2= \color{green}{1.96 } \\ 1.5^2 = \color{red}{2.25} $$ La migliore approssimazione con una cifra decimale per difetto è 1.4 mentre la migliore approssimazione per eccesso è 1.5.

In terza approssimazione, seguo lo stesso procedimento per cercare due numeri con due cifre decimali

$$ 1.41 < \sqrt{2} < 1.42 $$

Nota. Il procedimento per cercare i due estremi è sempre lo stesso. In questo caso l'estremo inferiore precedente è 1.4 $$ 1.40^2 = 1.96 \\ 1.41^2=\color{green}{1.9881} \\ 1.42^2 = \color{red}{2.0164} $$ La migliore approssimazione con due cifre decimali per difetto è 1.41 mentre la migliore approssimazione per eccesso è 1.42.

In quarta approssimazione cerco due numeri con tre cifre decimali

$$ 1.414 < \sqrt{2} < 1.415 $$

Nota. Ripeto lo stesso procedimento di ricerca. In questo caso l'estremo inferiore precedente è 1.41 $$ 1.410^2 = 1.9881 \\ 1.411^2 = 1.990921 \\ 1.412^2 = 1.993744 \\ 1.413^2 = 1.996569 \\ 1.414^2=\color{green}{1.999396} \\ 1.415^2 = \color{red}{2.002225} $$ La migliore approssimazione con due cifre decimali per difetto è 1.414 mentre la migliore approssimazione per eccesso è 1.415.

In quinta approssimazione cerco due numeri con quattro cifre decimali

$$ 1.4142 < \sqrt{2} < 1.4143 $$

In sesta approssimazione cerco due numeri con cinque cifre decimali

$$ 1.41421 < \sqrt{2} < 1.41422 $$

In settima approssimazione cerco due numeri con sei cifre decimali

$$ 1.414213 < \sqrt{2} < 1.414214 $$

In ottava approssimazione cerco due numeri con sette cifre decimali

$$ 1.4142135 < \sqrt{2} < 1.4142136 $$

A questo punto posso già fare due osservazioni

1. Le due approssimazioni per difetto e per eccesso si avvicinano progressivamente senza però mai essere uguali. Quindi, la radice quadrata di due non è un numero finito. E' un numero illimitato.
2. Le due approssimazioni sono numeri decimali illimitati senza un periodo che si ripete. Quindi, la radice quadrata di due non è un numero periodico. E' un numero non periodico.

In conclusione, la radice quadrata di due non è un numero finito, né un numero illimitato periodico.

Pertanto, √2 non appartiene all'insieme dei numeri razionali.

Quindi la radice quadrata √2 è un numero irrazionale ossia "non razionale".

E così via.