Formula di sdoppiamento dell'ellisse
Le formule di sdoppiamento mi permettono di determinare l'equazione della retta tangente in un punto dell'ellisse P(x0;y0). $$ \frac{xx_0}{a^2} + \frac{yy_0}{b^2} = 1 $$
Questa formula si può utilizzare soltanto se il punto P(x0;y0) è un punto dell'ellisse, non funziona se un punto esterno all'ellisse.
Se l'ellisse è centrata in un punto diverso dall'origine, l'equazione della retta tangente in un punto P(x0;y0) dell'ellisse si può calcolare usando quest'altra formula di sdoppiamento.
$$ A xx_0 + B yy_0 + C \frac{x+x_0}{2} + D \frac{y+y_0}{2} + E = 1 $$
In entrambi i casi si tratta di un'applicazione al caso dell'ellisse della formula di sdoppiamento delle coniche.
Esempio
Considero l'ellisse con l'equazione
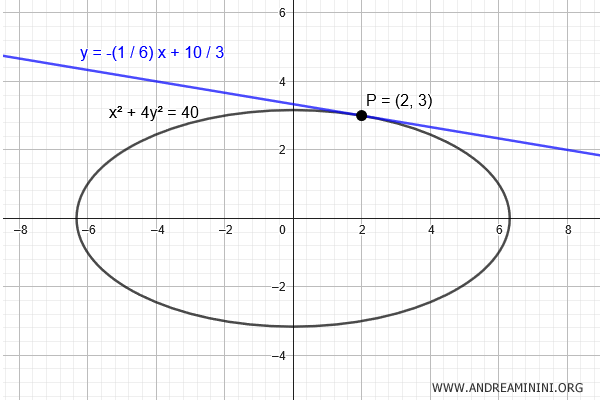
$$ x^2 + 4y^2 = 40 $$
La trasformo nella forma canonica dividendo entrambi i membri per 40
$$ \frac{ x^2 + 4y^2}{40} = \frac{ 40 }{40} $$
$$ \frac{ x^2}{40} + \frac{y^2}{10} = 1 $$
Dove a2=40 e b2=10
Devo calcolare l'equazione tangente all'ellisse nel punto (2;3)
$$ P(x_0;y_0) = (2;3) $$
Utilizzo la formula di sdoppiamento con le coordinate del punto sono x0=2 e y0=3.
$$ \frac{xx_0}{a^2} + \frac{yy_0}{b^2} = 1 $$
$$ \frac{x \cdot 2}{40} + \frac{y \cdot 3}{ 10 } = 1 $$
$$ \frac{x}{20} + \frac{y \cdot 3}{ 10 } = 1 $$
$$ y = \frac{10}{ 3 } \cdot ( 1 - \frac{x}{20} ) $$
$$ y = - \frac{1}{6}x + \frac{10}{ 3 } $$
Questa è la retta tangente nel punto P(2;3) dell'ellisse.
Esempio 2
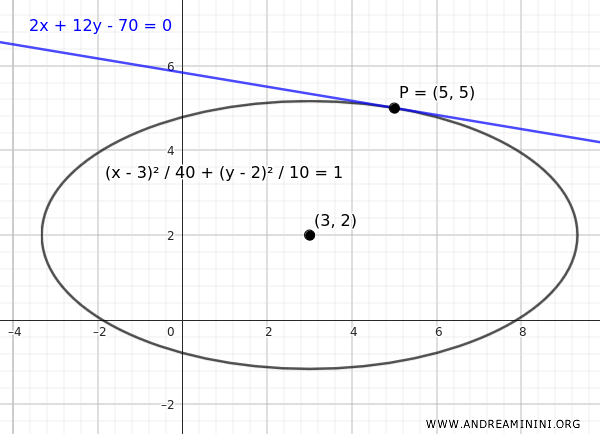
Considero una ellisse centrata nel punto P(3,2).
$$ \frac{ (x-3)^2}{40} + \frac{(y-2)^2}{10} = 1 $$
Trasformo l'equazione dell'ellise nella forma generale
$$ \frac{x^2-6x+9}{40} + \frac{y^2-4y+4}{10} = 1 $$
$$ \frac{x^2-6x+9}{40} + \frac{4 \cdot (y^2-4y+4)}{40} = 1 $$
$$ \frac{x^2-6x+9+ 4 \cdot (y^2-4y+4)}{40} = 1 $$
$$ x^2-6x+9+ 4 \cdot (y^2-4y+4) = 40 $$
$$ x^2-6x+9+ 4y^2-16y+16 = 40 $$
$$ x^2 + 4y^2 -6x-16y+16+9 - 40 = 0 $$
$$ x^2 + 4y^2 -6x-16y- 15 = 0 $$
Una volta raggiunta la forma generale $ Ax^2 + By^2 + Cx + Dy + E = 0 $, per trovare l'equazione della retta tangente nel punto $ P(x_0;y_0)=(5;5) $ sostituisco $ x^2 \rightarrow xx_0 $ e $ y^2 \rightarrow yy_0 $
$$ xx_0 + 4yy_0 -6x-16y- 15 = 0 $$
Poi sostituisco $ x \rightarrow \frac{x+x_0}{2} $ e $ y \rightarrow \frac{y+y_0}{2} $
$$ xx_0 + 4yy_0 -6 ( \frac{x+x_0}{2} ) -16 ( \frac{y+y_0}{2} )- 15 = 0 $$
$$ xx_0 + 4yy_0 -3 (x+x_0) -8 (y+y_0)- 15 = 0 $$
Infine sostituisco le coordinate del punto di tangenza $ P(x_0;y_0)=(5;5) $ ovvero $ x_0=5 $ e $ y_0=5 $
$$ x \cdot 5 + 4y \cdot 5 -3 (x+5) -8 (y+5)- 15 = 0 $$
$$ 5x +20y -3x - 15 - 8y - 40- 15 = 0 $$
$$ 2x +12 y - 70 = 0 $$
Quest'ultima è l'equazione della retta tangente all'ellisse nel punto $ P(5;5) $
La dimostrazione
Parto dall'equazione dell'ellisse:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Ipotizzo che una retta tangente a questa ellisse passi per il punto \((x_0, y_0)\) che sta sull'ellisse, quindi:
$$ \frac{x_0^2}{a^2} + \frac{y_0^2}{b^2} = 1 $$
Considero l'equazone di un fascio di rette che passa per il punto \((x_0, y_0)\):
$$ y = mx + c $$
Inserisco questa retta generica nell'equazione dell'ellisse:
$$ \frac{x^2}{a^2} + \frac{(mx + c)^2}{b^2} = 1 $$
$$ \frac{x^2}{a^2} + \frac{m^2x^2 + 2mxc + c^2}{b^2} = 1 $$
Moltiplico per \(a^2b^2\) per eliminare i denominatori
$$ b^2x^2 + a^2m^2x^2 + 2a^2mxc + a^2c^2 = a^2b^2 $$
Riorganizzo l'equazione in forma quadratica:
$$ (b^2 + a^2m^2)x^2 + 2a^2mxc + (a^2c^2 - a^2b^2) = 0 $$
Perché la retta sia tangente all'ellisse, il discriminante di questa equazione quadratica deve essere zero. Il discriminante \(\Delta\) per l'equazione quadratica \(Ax^2 + Bx + C = 0\) è dato da:
$$ \Delta = B^2 - 4AC $$
Dove $ A = b^2 + a^2m^2 $ , $ B = 2a^2mc $ e $ C = a^2c^2 - a^2b^2 $
Calcolo il discriminante:
$$ \Delta = (2a^2mc)^2 - 4(b^2 + a^2m^2)(a^2c^2 - a^2b^2) $$
Espando e semplifico:
$$ \Delta = 4a^4m^2c^2 - 4(b^2 + a^2m^2)(a^2c^2 - a^2b^2) $$
$$ \Delta = 4a^4m^2c^2 - 4[b^2a^2c^2 - b^2a^2b^2 + a^4m^2c^2 - a^4m^2b^2] $$
$$ \Delta = 4a^4m^2c^2 - 4b^2a^2c^2 + 4b^4a^2 - 4a^4m^2c^2 + 4a^4m^2b^2 $$
$$ \Delta = -4b^2a^2c^2 + 4b^4a^2 + 4a^4m^2b^2 $$
Perché il discriminante sia zero $ \Delta = 0 $:
$$ -4b^2a^2c^2 + 4b^4a^2 + 4a^4m^2b^2 = 0 $$
Divido per \(4a^2\):
$$ -b^2c^2 + b^4 + a^2m^2b^2 = 0 $$
Semplifico e ottengo:
$$ b^2(b^2 + a^2m^2) = b^2c^2 $$
Divido per \(b^2\):
$$ b^2 + a^2m^2 = c^2 $$
$$ c^2 = b^2 + a^2m^2 $$
Per trovare \(m\) e \(c\) in termini di \((x_0, y_0)\) so che \(y_0 = mx_0 + c\).
Da questa posso esprimere \(c\) come $ c = y_0 - mx_0 $$
Sostituisco \(c\) nell'equazione \(b^2 + a^2m^2 = c^2\):
$$ b^2 + a^2m^2 = (y_0 - mx_0)^2 $$
$$ b^2 + a^2m^2 = y_0^2 - 2y_0mx_0 + m^2x_0^2 $$
Riorganizzo per trovare \(m\):
$$ b^2 = y_0^2 - 2y_0mx_0 + m^2(x_0^2 - a^2) $$
Raccogo i termini di \(m\):
$$ b^2 = y_0^2 - 2y_0mx_0 + m^2(x_0^2 - a^2) $$
Ora isolo \(m\):
$$ y_0^2 - 2y_0mx_0 + m^2(x_0^2 - a^2) = b^2 $$
Porto tutto a sinistra per avere un'equazione quadratica in \(m\):
$$ m^2(x_0^2 - a^2) - 2y_0mx_0 + (y_0^2 - b^2) = 0 $$
Questa è un'equazione quadratica in \(m\). Posso risolverla usando la formula quadratica:
$$ m = \frac{-B \pm \sqrt{B^2 - 4AC}}{2A} $$
In questo caso $ A = x_0^2 - a^2 $ , $ B = -2y_0x_0 $ e $ C = y_0^2 - b^2 $
Per una retta tangente, il discriminante deve essere zero:
$$ B^2 - 4AC = 0 $$
Quindi:
$$ (-2y_0x_0)^2 - 4(x_0^2 - a^2)(y_0^2 - b^2) = 0 $$
$$ 4y_0^2x_0^2 - 4(x_0^2 - a^2)(y_0^2 - b^2) = 0 $$
$$ y_0^2x_0^2 = (x_0^2 - a^2)(y_0^2 - b^2) $$
Se risolvo questa equazione, posso trovare \(m\).
$$ y_0^2x_0^2 = (x_0^2 - a^2)(y_0^2 - b^2) $$
$$ y_0^2x_0^2 = x_0^2y_0^2 - x_0^2b^2 -y_0^2a^2 + a^2b^2 $$
$$ - x_0^2b^2 -y_0^2a^2 + a^2b^2 = 0 $$
$$ x_0^2b^2 + y_0^2a^2 = a^2b^2 $$
$$ \frac{ x_0^2b^2 }{a^2b^2} + \frac{y_0^2a^2}{a^2b^2} = \frac{ a^2b^2}{a^2b^2} $$
$$ \frac{ x_0^2 }{a^2} + \frac{y_0^2}{b^2} = 1 $$
Poiché \((x_0, y_0)\) è un punto sull'ellisse ed è anche un punto della retta tangente posso sostituire $ x_0^2 = x_0 \cdot x $ e $ y_0^2 = y_0 \cdot y $
$$ \frac{x_0 x}{a^2} + \frac{y_0 y}{b^2} = 1 $$
Questa equazione soddisfa la condizione di tangenza per ogni punto \((x_0, y_0)\) sull'ellisse.
E così via.
