Come determinare l'equazione dell'ellisse dati un fuoco e un semiasse
Per trovare l'equazione di un'ellisse centrata nell'origine O(0;0) conoscendo un fuoco F(xf;yf) e la lunghezza di un semiasse, posso usare il teorema di Pitagora.
Un esempio pratico
Considero un'elisse con centro nell'origine degli assi cartesiani $ O(0;0) $ di cui conosco un fuoco $ F(4;0) $ e la lunghezza del semiasse verticale $ b=3 $.
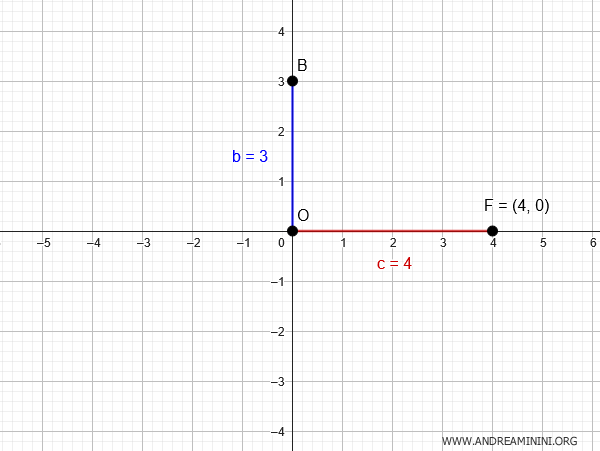
La distanza tra il fuoco e il centro mi restituisce la distanza focale $ c = 4 $
L'equazione dell'ellisse centrata nell'origine è
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Conosco già la lunghezza del semiasse verticale $ b=3 $, per completarla devo trovare anche quella del semiasse orizzontale.
Sapendo che la lunghezza del semiasse orizzontale $ a $ è uguale alla distanza tra il fuoco e il vertice B(0;3) del semiasse verticale, per determinarla posso usare il teorema di Pitagora.
$$ a^2 = \sqrt{b^2 + c^2} $$
Sostituisco $ b=3 $ e $ c=4 $
$$ a^2 = \sqrt{3^2 + 4^2} $$
$$ a^2 = \sqrt{9 + 16} $$
$$ a^2 = \sqrt{25} $$
$$ a = 5 $$
Quindi, i vertici sul semiasse orizzontale sono $ A(5;0) $ e $ A_2(-5;0) $ essendo simmetrici rispetto al centro $ O(0;0) $ dell'ellisse.
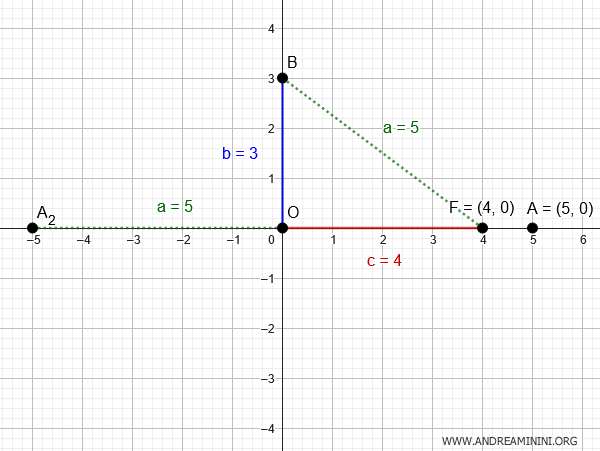
A questo punto ho tutti i dati necessari $ a=5 $ e $ b=3 $ per scrivere l'equazione dell'ellisse.
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{5^2} + \frac{y^2}{3^2} = 1 $$
$$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$
Ecco la rappresentazione grafica dell'equazione
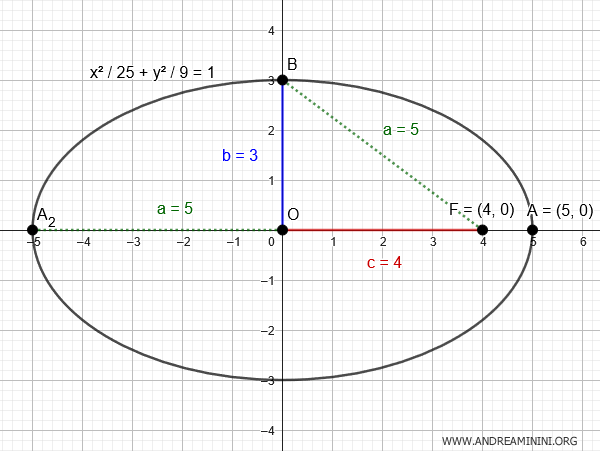
E così via.
