Come trovare l'equazione dell'ellisse dati due punti
Per determinare l'equazione di un'ellisse centrata nell'origine degli assi che passa per due punti (x1;y1) e (x2;y2) del piano, devo costruire un sistema con due equazioni generali dell'ellisse, sostituendo in ciascuna equazione le coordinate dei punti noti.
$$ \begin{cases} \frac{x_1^2}{a^2} + \frac{y_1^2}{b^2} = 1 \\ \\ \frac{x_2^2}{a^2} + \frac{y_2^2}{b^2} = 1 \end{cases} $$
La soluzione del sistema mi permette di trovare le lunghezze dei semiassi $ a $ e $ b $ dell'equazione dell'ellisse.
Un esempio pratico
In questo esercizio devo trovare l'equazione dell'ellisse che passa per i punti \( A \left( \sqrt{3}, \frac{1}{2} \right) \) e \( B \left( -1, \frac{\sqrt{3}}{2} \right) \)
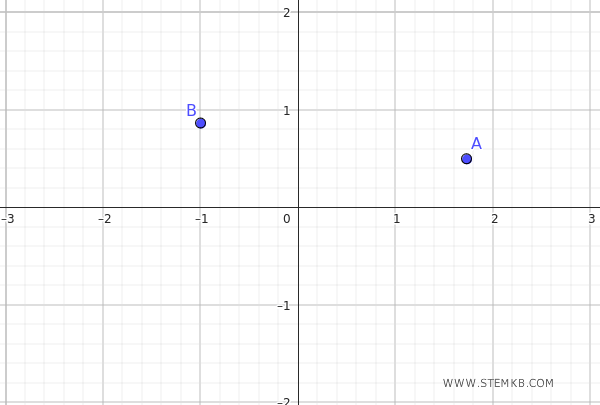
Parto dalla forma generale dell'equazione dell'ellisse con i suoi assi allineati agli assi cartesiani:
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
Dove \( a \) e \( b \) sono i semiassi maggiore e minore rispettivamente.
Devo trovare \( a^2 \) e \( b^2 \) in modo che l'ellisse passi per i punti dati.
Costruisco un'equazione per ciascun punto noto, sostituendo le coordinate $ x $ e $ y $ nell'equazione generale dell'ellisse.
Per il punto \( A \left( \sqrt{3}, \frac{1}{2} \right) \):
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{(\sqrt{3})^2}{a^2} + \frac{\left( \frac{1}{2} \right)^2}{b^2} = 1 $$
$$ \frac{3}{a^2} + \frac{ \frac{1}{4} }{b^2} = 1 $$
$$ \frac{3}{a^2} + \frac{1}{4} \cdot \frac{1}{b^2} = 1 $$
$$ \frac{3}{a^2} + \frac{1}{4b^2} = 1 $$
Per il punto \( B \left( -1, \frac{\sqrt{3}}{2} \right) \):
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{(-1)^2}{a^2} + \frac{\left( \frac{\sqrt{3}}{2} \right)^2}{b^2} = 1 $$
$$ \frac{1}{a^2} + \frac{ \frac{3}{4} }{b^2} = 1 $$
$$ \frac{1}{a^2} + \frac{3}{4} \cdot \frac{1}{b^2} = 1 $$
$$ \frac{1}{a^2} + \frac{3}{4b^2} = 1 $$
Ora costruisco un sistema di due equazioni con due incognite:
$$ \begin{cases} \frac{3}{a^2} + \frac{1}{4b^2} = 1 \\ \\ \frac{1}{a^2} + \frac{3}{4b^2} = 1 \end{cases} $$
Per risolverlo, posso eliminare una delle incognite. Moltiplico la prima equazione per 3:
$$ \begin{cases} 3 \left( \frac{3}{a^2} + \frac{1}{4b^2} \right) = 3 \\ \\ \frac{1}{a^2} + \frac{3}{4b^2} = 1 \end{cases} $$
$$ \begin{cases} \frac{9}{a^2} + \frac{3}{4b^2} = 3 \\ \\ \frac{1}{a^2} + \frac{3}{4b^2} = 1 \end{cases} $$
Ora sottraggo la seconda equazione dalla prima equazione del sistema.
$$ \left( \frac{9}{a^2} + \frac{3}{4b^2} \right) - \left( \frac{1}{a^2} + \frac{3}{4b^2} \right) = 3 - 1 $$
$$ \require{cancel} \frac{9}{a^2} + \cancel{ \frac{3}{4b^2} } - \frac{1}{a^2} - \cancel{ \frac{3}{4b^2} } = 2 $$
$$ \frac{9}{a^2} - \frac{1}{a^2} = 2 $$
$$ \frac{9-1}{a^2} = 2 $$
$$ \frac{8}{a^2} = 2 $$
$$ a^2 = 4 $$
$$ a = 2 $$
Ho trovato la lunghezza del semiasse orizzontale $ a $.
Adesso sostituisco \( a^2 = 4 \) in una delle equazioni originali del sistema per trovare $ b $
$$ \frac{1}{a^2} + \frac{3}{4b^2} = 1 $$
$$ \frac{1}{4} + \frac{3}{4b^2} = 1 $$
$$ \frac{3}{4b^2} = 1 - \frac{1}{4} $$
$$ \frac{3}{4b^2} = \frac{3}{4} $$
$$ 4 \cdot \frac{3}{4} = 3b^2 $$
$$ 3 = 3b^2 $$
Divido entrambi i lati per 3
$$ b^2 = 1 $$
$$ \sqrt{b^2} = \sqrt{1} $$
$$ b = 1 $$
Ho trovato anche la lunghezza del semiasse verticale $ b $.
Quindi, sapendo che $ a=2 $ e $ b=1$ l'equazione dell'ellisse è:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{2^2} + \frac{y^2}{1^2} = 1 $$
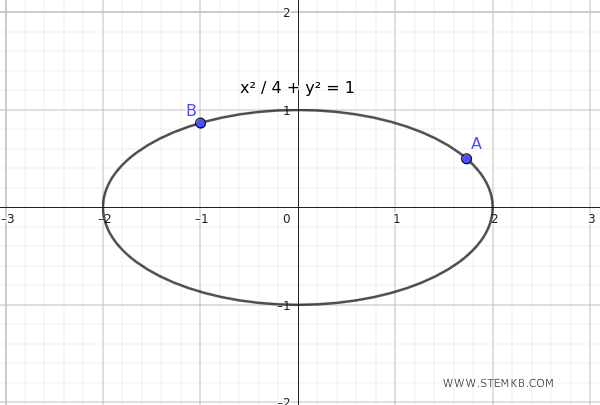
$$ \frac{x^2}{4} + y^2 = 1 $$
Questa equazione passa per i punti \( A \left( \sqrt{3}, \frac{1}{2} \right) \) e \( B \left( -1, \frac{\sqrt{3}}{2} \right) \)
E così via.
