Le rette tangenti a un'ellisse che passano per il punto P

Data un'ellisse e un punto qualsiasi P del piano, possono esistere due, una o nessuna retta tangente all'ellisse che passa per il punto P.

• Se il punto P è esterno all'ellisse, esistono due rette tangenti all'ellisse passanti per P.
  
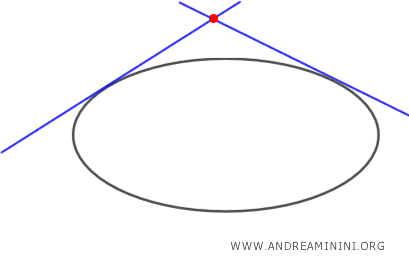
• Se il punto P è un punto dell'ellisse, esiste un'unica retta tangente all'ellisse che passa per P.
  
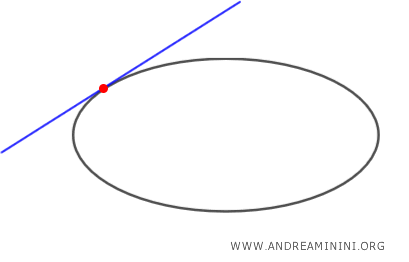
• Se il punto P è un punto interno all'ellisse, non esistono rette tangenti all'ellisse passanti per P.
  

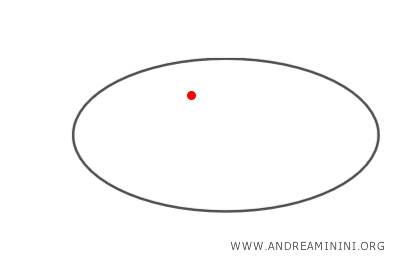
Come trovare le rette tangenti all'ellisse

Per trovare l'equazione delle rette tangenti all'ellisse che passano per P, scrivo l'equazione del fascio di rette che passa per il punto P(x₀,y₀)

$$ y−y_0=m(x−x_0) $$

Poi scrivo l'equazione dell'ellisse

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

Ora devo trovare quali rette del fascio hanno punti in comune con l'ellisse.

Costruisco un sistema con le due equazioni:

$$ \begin{cases}  y−y_0=m(x−x_0) \\ \\ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1  \end{cases} $$

Le soluzioni dell'equazione risolvente individuano tutti i punti di intersezione (tangenti e secanti) tra la retta e l'ellisse.

Sapendo che le rette tangenti hanno il discriminante nullo (un'unica soluzione), aggiungo la condizione $ \Delta = 0 $ per individuare solo le retti tangenti.

$$ \Delta = b^2-4ac=0 $$

Questa condizione mi permette di trovare il coefficiente angolare m delle rette tangenti all'ellisse, se esistono.

Una volta trovato il coefficiente angolare m, mi basta sostituirlo all'equazione del fascio di rette per trovare l'equazione della retta tangente.

Un esempio pratico

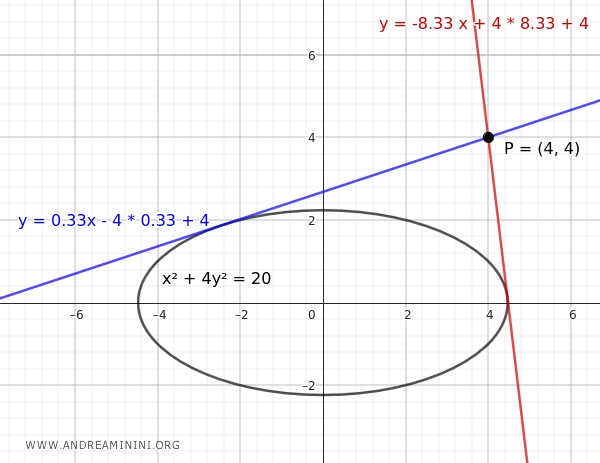
Considero un punto del piano P(4;4) e l'ellisse

$$ x^2 + 4y^2 = 20 $$

Devo capire se esistono delle rette tangenti all'ellisse che passano per il punto P(4;4) ed eventualmente trovare l'equazione delle rette.

Metto a sistema l'equazione della parabola con l'equazione del fascio di rette $ y - 0 = m (x-6) $ del punto P.

$$ \begin{cases} x^2 + 4y^2 = 20 \\ \\ y - 4 = m (x-4) \end{cases} $$

Ricavo la y nell'equazione risolvente e la sostituisco nell'equazione dell'ellisse

$$ \begin{cases} x^2 + 4[m(x-4)+4]^2 = 20 \\ \\ y = m (x-4)+4 \end{cases} $$

$$ \begin{cases} x^2 + 4[m(x-4)+4]^2 = 20 \\ \\ y = m (x-4)+4 \end{cases} $$

$$ \begin{cases} x^2 + 4[m^2(x-4)^2 + 2 \cdot 4 \cdot m(x-4)+16] = 20 \\ \\ y = m (x-4)+4 \end{cases} $$

$$ \begin{cases} x^2 + 4[m^2(x-4)^2 + 8m(x-4)+16] = 20 \\ \\ y = m (x-4)+4 \end{cases} $$

$$ \begin{cases} x^2 + 4m^2(x-4)^2 + 32m(x-4)+64 = 20 \\ \\ y = m (x-4)+4 \end{cases} $$

$$ \begin{cases} x^2 + 4m^2(x^2 - 8x +16) +32mx - 128m +64 - 20 = 0 \\ \\ y = m (x-4)+4 \end{cases} $$

$$ \begin{cases} x^2 + 4m^2x^2 - 32m^2x +64m^2 +32mx - 128m +44 = 0 \\ \\ y = m (x-4)+4 \end{cases} $$

$$ \begin{cases} x^2 (1 + 4m^2) + x( - 32m^2+32m) +64m^2 - 128m +44 = 0 \\ \\ y = m (x-4)+4 \end{cases} $$

Aggiungo la condizione di tangenza $ \Delta = 0 $

$$ \Delta = b^2 - 4ac = 0 $$

Dove $ a=1+ 4m^2 $ , $ b = - 32m^2+32m  $, $ c = 64m^2 - 128m +44 $$

$$ \Delta = ( - 32m^2+32m )^2 - 4(1+ 4m^2) \cdot ( 64m^2 - 128m +44 )  = 0 $$

$$ \Delta =  1024m^4 - 2048m^3 + 1024m^2 - 1024m^4 + 2048m^3 - 960m^2 + 512m - 176 = 0  $$

$$ \Delta =  64m^2 + 512m - 176 = 0  $$

Questa è una equazione quadratica in \( m \) che posso risolvere usando la formula risolutiva delle equazioni quadratiche:

$$ m = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

Dove \( a = 64 \), \( b = 512 \), e \( c = -176 \):

$$ m = \frac{-512 \pm \sqrt{512^2 - 4 \cdot 64 \cdot (-176)}}{2 \cdot 64} $$

$$ m = \frac{-512 \pm \sqrt{262144 + 45056}}{128} $$

$$ m = \frac{-512 \pm \sqrt{307200}}{128} $$

$$ m = \frac{-512 \pm 554.256}{128} $$

Calcolo i due valori di \( m \):

$$ m_1 = \frac{-512 + 554.256}{128} = \frac{42.256}{128} \approx 0.33 $$

$$ m_2 = \frac{-512 - 554.256}{128} = \frac{-1066.256}{128} \approx -8.33 $$

Quindi, i valori di \( m \) che soddisfano la condizione di tangenza sono:

$$ m \approx 0.33 \quad \text{e} \quad m \approx -8.33 $$

Ora, con questi valori di \( m \), possiamo trovare le coordinate \( (x, y) \) corrispondenti utilizzando l'equazione della retta $ y = mx - 4m + 4 $

• Se $ m \approx 0.33 $ l'equazione della retta tangente è $$ y = 0.33 \cdot x - 4 \cdot 0.33 + 4 $$
• Se $ m \approx -8.33 $ l'equazione della retta tangente è $$ y =-8.33 \cdot x - 4 \cdot (-8.33) + 4 $$ $$ y =-8.33 \cdot x + 4 \cdot 8.33 + 4 $$

Entrambe le rette sono tangenti all'ellisse e passano per il punto P(4;4).

E così via.