Equazione dell'ellisse non centrata all'origine degli assi cartesiani
L'equazione dell'ellisse con centro (x0;y0) diverso dall'origine degli assi cartesiani è $$ \frac{(x-x_0)^2}{a^2} + \frac{(y-y_0)^2}{b^2} = 1 $$ detta forma canonica traslata.
In alternativa, l'equazione di un'ellisse non centrata all'origine degli assi può essere scritta anche in questa forma generale.
$$ Ax^2 + By^2 +Cx + Dy + E = 0 $$
Dove
$$ A = b^2 $$
$$ B = a^2 $$
$$ C = -2b^2x_0 $$
$$ D = -2a^2y_0 $$
$$ E = b^2x_0^2 + a^2y_0 -a^2b^2 $$
Le coordinate del centro dell'ellisse traslata sono:
$$ O \left( - \frac{c}{2a} ; - \frac{d}{2b} \right) $$
Quindi, gli assi di simmetria dell'ellisse
$$ x = - \frac{c}{2a} $$
$$ y = - \frac{d}{2b} $$
In altre parole una ellisse con centro diverso dall'origine è semplicemente una traslazione di un'ellisse centrata nell'origine.
Un esempio pratico
Considero un'ellisse con semiassi \(a = 3\) e \(b = 2\), e il centro dell'ellisse nel punto \((x_0, y_0) = (1, -2)\).
L'equazione dell'ellisse in forma canonica traslata con $ x_0 = 1 $ e $ y_0 = -2 $ è la seguente:
$$ \frac{(x - x_0)^2}{a^2} + \frac{(y - y_0)^2}{b^2} = 1 $$
$$ \frac{(x - 1)^2}{3^2} + \frac{(y + 2)^2}{2^2} = 1 $$
$$ \frac{(x - 1)^2}{9} + \frac{(y + 2)^2}{4} = 1 $$
Ecco la rappresentazione grafica
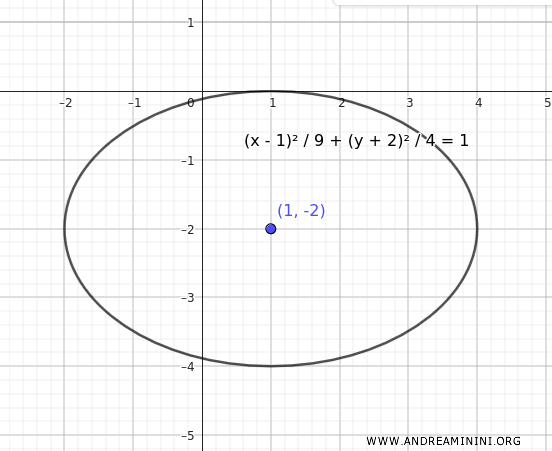
Da notare che questa ellisse è semplicemente una traslazione di un'ellisse centrata nell'origine.
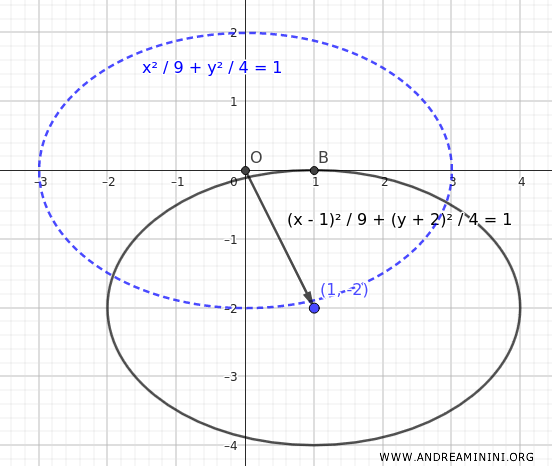
Ora converto questa equazione nella forma generale:
$$ Ax^2 + By^2 + Cx + Dy + E = 0 $$
Dove:
$$ A = b^2 = 2^2 = 4 $$
$$ B = a^2 = 3^2 = 9 $$
$$ C = -2b^2x_0 = -2 \cdot 4 \cdot 1 = -8 $$
$$ D = -2a^2y_0 = -2 \cdot 9 \cdot (-2) = 36 $$
$$ E = b^2x_0^2 + a^2y_0^2 - a^2b^2 = 4 \cdot 1^2 + 9 \cdot (-2)^2 - 9 \cdot 4 $$
$$ E = 4 \cdot 1 + 9 \cdot 4 - 36 $$
$$ E = 4 + 36 - 36 $$
$$ E = 4 $$
Quindi, l'equazione generale dell'ellisse è:
$$ 4x^2 + 9y^2 - 8x + 36y + 4 = 0 $$
Dal punto di vista grafico la rappresentazione è la stessa.
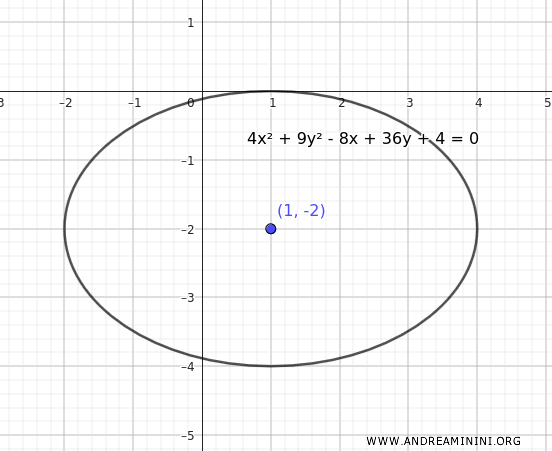
A questo punto controllio che il centro dell'ellisse sia effettivamente \((1, -2)\) utilizzando le formule per il centro \((h, k)\):
$$ h = -\frac{C}{2A} = -\frac{-8}{2 \cdot 4} = \frac{8}{8} = 1 $$
$$ k = -\frac{D}{2B} = -\frac{36}{2 \cdot 9} = -\frac{36}{18} = -2 $$
Le coordinate del centro sono confermate: \((1, -2)\).
Quindi, ho verificato che le due forme dell'equazione descrivono la stessa ellisse con centro \((1, -2)\), semiassi \(a = 3\) e \(b = 2\).
La dimostrazione
Per dimostrare l'equazione canonica e generale di un'ellisse non centrata negli assi cartesiani, parto dall'equazione di un'ellisse centrata nell'origine degli assi
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
A questo punto ricorro a una trasformazione geometrica per spostare tutti i punti dell'ellisse, facendo in modo che i punti mantengano le stesse distanze tra loro (isometria).
In questo caso mi serve una traslazione
$$ \begin{cases} x' = x+x_0 \\ \\ y' = y+y_0 \end{cases} $$
Dove x' e y' sono le nuove coordinate di ogni punto (x;y) mentre x0 e y0 misurano lo spostamento orizzontale e verticale.
Ricavo i valori di x' e y'
$$ \begin{cases} x =x' - x_0 \\ \\ y = y' - y_0 \end{cases} $$
Sostituisco $ x =x' - x_0 $ e $ y = y' - y_0 $ nell'equazione canonica dell'ellisse.
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{(x' - x_0)^2}{a^2} + \frac{(y' - y_0)^2}{b^2} = 1 $$
Ho così' ottenuto l'equazione canonica dell'ellisse centrata nel punto $ (x_0;y_0) $.
Ora svolgo i calcoli algebrici
$$ \frac{x'^2 - 2x'x_0 + x_0^2}{a^2} + \frac{ y'^2 - 2y'y_0 + y_0^2 }{b^2} = 1 $$
$$ \frac{b^2 (x'^2 - 2x'x_0 + x_0^2) + a^2 (y'^2 - 2y'y_0 + y_0^2) }{a^2b^2} = 1 $$
$$ b^2 (x'^2 - 2x'x_0 + x_0^2) + a^2 (y'^2 - 2y'y_0 + y_0^2) = a^2b^2 $$
$$ b^2 (x'^2 - 2x'x_0 + x_0^2) + a^2 (y'^2 - 2y'y_0 + y_0^2) - a^2b^2 = 0 $$
$$ x'^2b^2 - 2x'x_0b^2 + x_0^2b^2 + y'^2a^2 - 2y'y_0a^2 + y_0^2a^2 - a^2b^2 = 0 $$
$$ x'^2 \cdot (b^2) + y'^2 \cdot (a^2) +x' \cdot ( - 2x_0b^2 ) + y' \cdot ( - 2y_0a^2 ) + x_0^2b^2 + y_0^2a^2 - a^2b^2 = 0 $$
Ora sostituisco $ A = b^2 $, $ B=a^2 $ , $ C = -2b^2x_0 $ , $ D = -2a^2y_0 $ , $ E = b^2x_0^2 + a^2y_0 -a^2b^2 $
$$ x'^2 \cdot A + y'^2 \cdot B +x' \cdot C + y' \cdot D + E = 0 $$
$$ Ax'^2 + By'^2+ Cx' + Dy' + E = 0 $$
Ho così ottenuto l'equazione generale dell'ellisse centrata nel punto $ (x_0;y_0) $.
E così via.
